Представление рынка МБК в виде сети контрагентов: основные понятия

межбанковский кредитование рынок банкротство В продолжение рассмотрения основ описания структуры рынка МБК необходимо подчеркнуть, что наше и многие существующие исследования рынков МБК тем или иным образом опираются на теорию сетей, или графов, и ее терминологию См. напр.: Iazzetta C., Manna M. The Topology of The Interbank Market: Developments in Italy since 1990 // Banca d’Italia Working Papers. № 711. 2009. 33 p.; De Masi G., Iori G., Caldarelli G. The Italian Interbank Network: Statistical Properties and a Simple Model // SPIE Proceedings. Volume 6601 «Noise and Stochastics in Complex Systems and Finance». June 2007. 14 p. В соответствии с ней, банки-контрагенты на рынке представляются в виде узлов, или вершин, графа. Направленные ребра графа обозначают существующие связи банков на рынке МБК, то есть отношения «заемщик-кредитор» или «кредитор-заемщик» между двумя банками В данной работе входящие в узел ребра означают отношения «кредитор-заемщик», исходящие — отношения «заемщик-кредитор», хотя в литературе могут встречаться обратные обозначения. Вес направленного ребра представляет суммарный объем займа одного банка у другого на рынке. Число входящих или исходящих связей (ребер) банка-узла с остальными банками-участниками рынка МБК называется входящей или исходящей степенью (degree) узла.

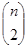
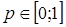
Работой, которая стала базой для многих последующих исследований в теории сетей, является модель П. Эрдеша и А. Реньи Erdцs P., Rйnyi A. On Random Graphs I // Publicationes Mathematicae. Vol. 6. 1959. Pp. 290−297., впервые изучивших случайные графы. Их первоначальная модель G (n, N) предполагает равную вероятность для каждой реализации случайного графа, то есть для каждого графа, выбираемого случайным образом из всех возможных графов, имеющих n узлов, которые соединены между собой N ребрами В исходной модели авторов ребра не направлены, то есть между двумя узлами может быть только одно ребро. Было также предложено несколько вариантов их модели, из которых, как отмечают исследователи Newman M.E.J. Random Graphs as Models of Networks // Santa Fe Institute Working Papers. 2002;02−005. P. 1., наиболее часто применяемым и изученным служит модель G (n, p). В ней каждое возможное ребро между каждыми двумя узлами включается в граф с одинаковой заданной вероятностью p, независимой от наличия других ребер и называемой вероятностью Эрдеша-Реньи. Построение случайного графа в данном случае выглядит следующим образом Описание на основе: Берновский М. М., Кузюрин Н. Н. Случайные графы, модели и генераторы безмасштабных графов // Труды Института системного программирования РАН. Том 22. 2012. С. 419−432.: фиксируется натуральное число n, которое задает множество вершин случайного графа Р1, Р2, …, Рn. Задается полный граф Гn (граф, где каждые две вершины соединены ребром) на указанном множестве вершин, с пронумерованными ребрами из N =. Задается также значение вероятности и выбираются ребра из множества всех ребер на основе схемы Бернулли (независимых испытаний) с постоянной вероятностью появления ребра между каждыми двумя ребрами, равной р. Таким образом, получается случайный граф G (n, p), формально являющийся вероятностным пространством, в котором каждая реализация случайного графа появляется с одинаковой вероятностью, соответствующей заданному числу вершин графа.

Следует отметить, что существуют и другие модели формирования сетей, включая, например, подходы с точки зрения теории игр, где игроки выбирают контрагентов, оценивая выгоды (платежи) от наличия связей См. например: Allen F., Babus A. Networks in Finance // The Network Challenge: Strategy, Profit, and Risk in an Interlinked World / Ed. by P.R. Kleindorfer, Y. Wind. — Upper Saddle River: Pearson Education, 2009. P. 367−382; Cohen-Cole E., Patacchini E., Zenou Y. Systemic Risk and Network Formation in the Interbank Market // CAREFIN Research Paper. January 2013. Retrieved from: http://people.su.se/~yvze0888/Cohen_Patacchini_Zenou₂₅.pdf, а также модель предпочтительного присоединения (preferential attachment), название которой дали А.-Л. Барабаши и Р. Альберт Albert R., Barabasi A.-L. Statistical Mechanics of Complex Networks // Reviews of Modern Physics. Volume 74. January 2002. Pp. 47−97. и на которой мы остановимся подробнее. Модель начинается с небольшого числа узлов m0 Предполагается, что изначально m0и степень каждого присутствующего узла не меньше 1 (в противном случае при росте сети узел всегда будет оставаться не связанным с остальными узлами)., к которым на каждом временном шаге добавляется новый узел, соединяемый с т присутствующими в сети узлами т ребрами (при этом тт0) исходя из того, что вероятность Р (ki) того, что новый узел будет соединен с уже имеющимся в сети узлом i, зависит от степени ki узла i: Р (ki) =, где в знаменателе — сумма степеней всех уже присутствующих в сети узлов. Таким образом, наблюдается «предпочтительное присоединение» новых узлов к тем узлам, степени которых в сети наиболее высоки. Как заметили А.-Л. Барабаши и Р. Альберт, в сетях, создаваемых в соответствии с их моделью, распределение степеней узлов подчиняется степенному закону, то есть такие сети являются безмасштабными. Примененный А.-Л. Барабаши и Р. Альбертом механизм предпочтительного присоединения часто успешно использовался исследователями для объяснения формирования таких видов реально существующих сетей, как Всемирная паутина, социальные сети, сеть цитирования научных журналов и т. д., в то время как ее применимость для генерации сети, представляющей рынок МБК, не совсем однозначна: в частности, Ж. Де Мази и другими De Masi G., Iori G., Caldarelli G. A Fitness Model for the Italian Money Market // Report № 06/08. London, City University, Department of Economics. 2006. 5 p. было отмечено, что механизм предпочтительного присоединения не подходит для описания создания сети, соответствующей рынку МБК Италии.

В нашем исследовании будет применена модель с использованием вероятности Эрдеша-Реньи, дающая возможность проанализировать различные варианты структуры рынка МБК (при изменении величины параметра p, а также изменении других ключевых параметров, касающихся устройства и участников рынка), сконцентрировавшись на влиянии основных параметров рынка на его устойчивость Оборотной стороной возможности реализовать разнообразные структуры рынка по модели Эрдеша-Реньи является упрощенность представления банковской системы; однако анализ влияния ключевых характеристик рынка может быть произведен в соответствии с ней, а влияние на устойчивость более подробных характеристик рынка могут стать предметом будущих исследований автора. К тому же развитие модели с некоторыми простыми предпосылками позволяет проанализировать структуру рынка с различными типами участников, не слишком сложную, но довольно схожую с действительным положением вещей (о чем подробнее будет сказано в параграфе 2.1). Осуществить реализации случайного графа с определенными задаваемыми параметрами нам позволит программа FlowNetwork 2.0, созданная представителями Банка Англии и предназначенная как раз для анализа устойчивости рынка взаимосвязанных финансовых агентов (рынка МБК) к шокам и распространению банкротств. Механизм создания сети и анализа распространения банкротств через данную программу соответствует подробно описанному в Главе 2 данной работы.