Методы моделирования. 
Методы принятия управленческих решений

К основным методам моделирования, используемым на этапе диагностики проблем, относятся: экономико-математическое моделирование, теория очередей, теория запасов, экономический анализ.

Экономико-математическое моделирование основывается на использовании однои многофакторных моделей. Применяются однофакторные модели следующих видов: линейные модели, парабола и гипербола; многофакторные модели: линейная и логарифмическая. Наиболее часто применяются линейные модели — однофакторные:

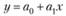
и многофакторные:

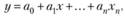
где у — зависимая переменная, описывающая последствия принимаемых решений; а0, а1, …, aп — параметры уравнений; х, x1, …, хn - независимые переменные при принятии решений. Задача состоит в определении параметров уравнения а0, а1, …, aп.

Теория очередей (теория массового обслуживания) применяется для решений, связанных с ситуациями ожидания. Она помогает принять решение, устанавливающее определенное равновесие между размерами упущенной выгоды (доходов) и величиной дополнительных затрат в сервисных организациях, таких как банки, магазины, железнодорожные и авиационные кассы, поликлиники, автозаправочные станции, ремонтные фирмы, парикмахерские, телефонные станции. Клиенты, не желающие стоять в очереди, представляют упущенную выгоду. Время ожидания можно сократить за счет увеличения количества операторов, обслуживающих систему, что ведет к увеличению затрат. В основе расчетов лежит известная формула Пуассона:

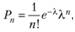
где Рn — вероятность появления n-го количества клиентов; е — основание натурального логарифма, е = 2,7183…;? — среднее количество клиентов; п — количество клиентов в единицу времени.

Основными характеристиками модели теории очередей являются количество каналов обслуживания, среднее время обслуживания одного клиента, количество клиентов, время ожидания обслуживания и др. На основе выполненных расчетов определяется необходимое количество каналов обслуживания при допустимом, с точки зрения клиента, ожидании обслуживания.

Важная характеристика систем массового обслуживания — время обслуживания требований в системе. Время обслуживания одного требования — это, как правило, случайная величина и, следовательно, может быть описано законом распределения. Наибольшее распространение в теории, особенно в практических приложениях, получил экспоненциальный закон распределения времени обслуживания. Функция распределения для этого закона имеет вид.

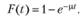
Иными словами, вероятность того, что время обслуживания не превосходит некоторой величины t, определяется этой формулой, где? — параметр экспоненциального закона распределения времени, необходимого для обслуживания требований в системе, т. е. величина, обратная среднему времени обслуживания tоб:

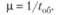
Наиболее распространены системы массового обслуживания с ожиданием, т. е. такие системы, в которых требования, поступившие в момент, когда все обслуживающие каналы заняты, ставятся в очередь и обслуживаются по мере освобождения каналов.

Общая постановка задачи состоит в следующем. Система имеет т обслуживающих каналов, каждый из которых может одновременно обслуживать только одно требование. В систему поступает простейший (пуассоновский) поток требований с параметром ?.

Если в момент поступления очередного требования в системе на обслуживании уже находится не меньше т требований (т.е. все каналы заняты), то это требование становится в очередь и ждет начала обслуживания.

Время обслуживания каждого требования t?6 — случайная величина, которая подчиняется экспоненциальному закону распределения с параметром ?.

Системы массового обслуживания с ожиданием можно разбить на две большие группы: замкнутые (с ограниченной длиной очереди) и разомкнутые (с неограниченной очередью). К замкнутым относятся системы, в которых поступающий поток требований возникает, как правило, в самой системе и ограничен. Если в канале обслуживания возникает очередь с бесконечным числом требований, то системы называются разомкнутыми. Примерами подобных систем могут служить магазины, кассы вокзалов, портов. Для этих систем поступающий поток требований можно считать неограниченным.

Отмеченные особенности функционирования систем этих двух видов накладывают определенные условия на используемый математический аппарат. Расчет характеристик работы систем массового обслуживания различного вида может быть проведен на основе расчета вероятностей состояний систем (так называемые формулы Эрланга).

При изучении таких систем рассчитывают различные показатели эффективности обслуживающей системы. В качестве основных показателей могут быть вероятность того, что все каналы свободны или заняты, математическое ожидание длины очереди (средняя длина очереди), коэффициенты занятости и простоя каналов обслуживания и др.

Важнейшие характеристики работы систем массового обслуживания:

1) вероятность того, что все обслуживающие каналы свободны:

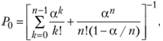
где п — количество клиентов; k — число обслуживающих каналов;? = ?/? — среднее число каналов, которое необходимо иметь, чтобы обслуживать в единицу времени все поступающие требования,? — среднее число требований, поступающих за единицу времени, 1/? — среднее время обслуживания одним каналом одного требования;

2) вероятность того, что занято ровно k обслуживающих каналов при условии, что общее число требований, находящихся на обслуживании, не превосходит числа обслуживающих аппаратов:

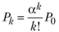при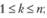

3) вероятность того, что в системе находится k требований в случае, когда их число больше числа обслуживающих каналов:

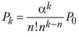при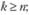

4) вероятность того, что все обслуживающие канаты заняты:

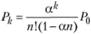при

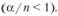
Условие ?/п < 1 означает, что число обслуживающих каналов должно быть больше среднего числа каналов, необходимых для того, чтобы за единицу времени обслужить все поступившие требования;

5) среднее время ожидания требования в системе:

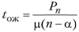при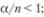

6) средняя длина очереди:

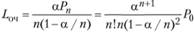при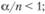

7) среднее число свободных от обслуживания каналов:

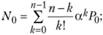
8) коэффициент простоя каналов:

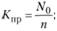
9) среднее число занятых обслуживанием каналов:

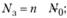
10) коэффициент загрузки каналов:

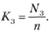
Рассмотрим пример системы массового обслуживания с очередью, где? — среднее число требований, поступающих за единицу времени; l/? — среднее время обслуживания одним каналом одного требования, тогда ос = ?/? — среднее число каналов, которое необходимо иметь, чтобы обслуживать в единицу времени все поступающие требования. Поэтому условие ?/п < 1 означает, что число обслуживающих каналов должно быть больше среднего числа каналов, необходимых для того, чтобы за единицу времени обслужить все поступившие требования.

Пример. Повседневными задачами ИТ-службы является обеспечение работоспособности ИТ-инфраструктуры, предоставление информационных услуг и своевременное разрешение инцидентов.

Инцидент — это любое событие, не являющееся частью стандартных операций по предоставлению услуги, которое привело или может привести к нарушению или снижению качества этой услуги. В методологии управления ИТ-процессами под инцидентами понимаются не только ошибки аппаратного или программного обеспечения, но и запросы на обслуживание. Запрос на обслуживание (service request) — это запрос от пользователя на поддержку, предоставление информации, консультации или документации, не являющийся сбоем ИТ-инфраструктуры. Таким образом, классическая задача теории массового обслуживания, решенная сотрудником Копенгагенской телефонной компании А. Эрлангом (1878−1929), в терминологии менеджмента инцидентов может быть описана следующим образом.

Пусть т специалистам службы поддержки поступает простейший поток обращений интенсивностью ?. Если в момент поступления обращения есть хотя бы один свободный специалист, то он немедленно принимается за работу. Если все специалисты заняты, то обращение становится в очередь за требованиями, которые поступили раньше. Освободившийся специалист принимается за разрешение очередного инцидента. Каждый инцидент решается только одним специалистом. Специалист решает в каждый момент времени не более одного инцидента. Длительность обслуживания представляет собой случайную величину с одним и тем же законом распределения вероятностей.

Таким образом, менеджмент инцидентов является классическим примером системы массового обслуживания с очередью: инцидент регистрируется в системе, разрешается, а затем закрывается. Тогда модель, построенная с использованием теории массового обслуживания, должна описывать связь между средним временем работы специалистов технической поддержки и средним временем разрешения инцидента, а также производительностью системы и давать ответы на вопрос: какова стоимость простоя клиентов в очереди на обслуживание и стоимость содержания дополнительных ИТ-сотрудников?

Для решения данной задачи необходимо определить параметры входного потока требований на обслуживание, описываемого законом Пуассона. Предположим, проведены хронометражные замеры о потоке требований на обслуживание в единицу времени, которые показали, что среднее число инцидентов в единицу времени? = 0,903 инцидента/мин.

Предположим далее, что закон распределения вероятностей длительности обслуживания является экспоненциальным, а средняя продолжительность обслуживания одного инцидента равна 1,6 мин. Тогда интенсивность обслуживания составит, инцидентов/мин:

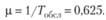
Если ??, как в нашем случае (0,903 > 0,625), то в службе поддержки образуется очередь.

Точно определить величину очереди как случайную нельзя. Можно вычислить вероятность Pn(t) того, что в момент времени t очередь будет характеризоваться числом требований п.

Определим среднее время ожидания (Tс), которое складывается из среднего времени ожидания обслуживания в очереди (Tож) и среднего времени обслуживания (Тобсл):

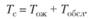
В том случае, когда в системе работают п операторов, среднее время пребывания заявки в очереди (Тож) и среднее время пребывания заявки в системе (Tс) находятся по формулам Литтла:

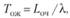
где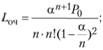

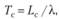
где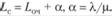

В нашем случае, а = 0,903 / 0,625 = 1,4448; при п = 2 время пребывания заявки в очереди Тож = 1,6 мин, а время пребывания заявки в системе Тс = 3,2 мин; при п = 3 время пребывания заявки в очереди Тож = 0,2 мин, а время пребывания заявки в системе Тс = 1,8 мин; при п = 4 время пребывания заявки в очереди Тож - 0,04 мин, а время пребывания заявки в системе Тс = 1,64 мин.

Предположим, что потери от простоев сотрудника из-за возникшего инцидента составляют 0,05 долл./мин, а содержание одного специалиста в центре технической поддержки — 0,04 долл./мин. За период времени Т в систему поступает ?Т инцидентов, т. е. 1,445 заявок на обслуживание в минуту.

Потери вследствие простоя сотрудников при различном числе специалистов центра технической поддержки, расходы на их заработную плату, а также суммарные затраты и потери в час приведены в табл. 4.2.

Таблица 4.2

Данные о расходах

Из табл. 4.2 очевидно, что при таком потоке инцидентов экономически целесообразно иметь в центре технической поддержки трех специалистов, поскольку суммарные затраты и потери будут наименьшими и составлять 0,25 долл./мин, или 2880 долл./мес.

При рассмотрении замкнутых систем массового обслуживания к постановке задачи следует добавить условие: поток поступающих требований ограничен, т. е. в системе одновременно не может находиться больше т требований (т — число обслуживаемых объектов).

Теория запасов была разработана в начале XX столетия, а широкое применение началось с 1940;х гг. Наибольших успехов, как правило, достигали японские предприятия. Использование теории запасов позволяет установить равновесие между затратами на создание запасов и издержками, связанными с потерями в случае нарушения производственного процесса. Запасы называют «бездействующими ресурсами» (idle resource), они подвержены порче, хищениям, устареванию и пр. Кроме того, они увеличивают расходы на оборотные средства предприятия. Теория запасов позволяет определить экономически выгодный размер запаса (economic order quantity) по формуле, разработанной Ф. Гаррисоном в 1915 г.:

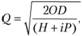
где О — затраты на оформление заказа (order cost); D — годовые запасы; Я — издержки хранения (holding cost); i — начисления к стоимости хранящихся запасов (определяется как отношение дохода, который можно было бы получить от вложения капитала на другие цели, к величине стоимости запасов); Р — стоимость хранящихся запасов (price).

Экономически выгодный размер запаса является таким количеством запаса, который позволяет свести к минимуму общие издержки, связанные с хранением запаса.

Математические модели управления запасами позволяют найти оптимальный уровень запасов некоторого товара, минимизирующий суммарные затраты на покупку, оформление и доставку заказа, хранение товара, а также убытки от его дефицита.

Модель Уилсона является простейшей моделью управления запасами и описывает ситуацию закупки продукции у внешнего поставщика, которая характеризуется следующими допущениями:

• • интенсивность потребления является априори известной и постоянной величиной;
• • заказ доставляется со склада, на котором хранится ранее произведенный товар;
• • время поставки заказа является известной и постоянной величиной;
• • каждый заказ поставляется в виде одной партии;
• • затраты на осуществление заказа не зависят от размера заказа;
• • затраты на хранение запаса пропорциональны его размеру;
• • отсутствие запаса (дефицит) является недопустимым.

Входные параметры модели Уилсона:

• 1) v — интенсивность (скорость) потребления запаса (ед. товаров / ед. времени);
• 2) s — затраты на хранение запаса (руб. / ед. товаров? ед. времени);
• 3) К — затраты на осуществление заказа, включающие в себя оформление и доставку заказа (руб.);
• 4) tд — время доставки заказа (ед. времени).

Выходные параметры модели Уилсона:

• 1) Q — размер заказа (ед. товаров);
• 2) L — общие затраты на управление запасами в единицу времени, (руб. / ед. времени);
• 3)? — период поставки, т. е. время между подачами заказа или между поставками (ед. времени);
• 4) h0 — точка заказа, т. е. размер запаса на складе, при котором надо подавать заказ на доставку очередной партии.

Циклы изменения уровня запаса в модели Уилсона графически представлены на рис. 4.3. Максимальное количество продукции, которая находится в запасе, совпадает с размером заказа Q.

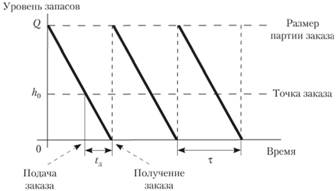
Рис. 4.3. График циклов изменения запасов в модели Уилсона [24].

Формула Уилсона определяет оптимальный размер заказа:

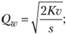
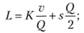
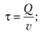
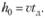
График затрат на управление запасами в модели Уилсона представлен на рис. 4.4.

Модель планирования экономичного размера партии представляет собой модифицированную модель Уилсона, используемую для моделирования процессов закупки продукции у внешнего поставщика. Ее можно применять в случае собственного производства продукции. Некоторый производственный процесс схематично представлен на рис. 4.5. На первом станке производится партия деталей с интенсивностью X деталей в единицу времени, которые используются на втором станке с интенсивностью v (деталей / ед. времени).

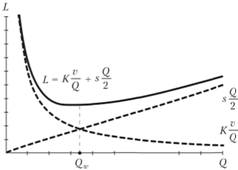
Рис. 4.4. График затрат на управление запасами в модели Уилсона [24].

Входные параметры модели планирования экономичного размера партии:

• 1) X — интенсивность производства продукции первым станком (ед. товаров / ед. времени);
• 2) v — интенсивность потребления запаса (ед. товаров / ед. времени);
• 3) s — затраты на хранение запаса (руб. / ед. товаров? ед. времени);
• 4) К — затраты на осуществление заказа, включающие в себя подготовку (переналадку) первого станка для производства продукции, потребляемой на втором станке (руб.);
• 5) tп — время подготовки производства (переналадки) (ед. времени).

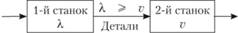
Рис. 4.5. Схема производственного процесса.

Выходные параметры модели планирования экономичного размера партии:

• 1) Q — размер заказа (ед. товаров);
• 2) L — общие затраты на управление запасами в единицу времени (руб. / ед. времени);
• 3) ? — период запуска в производство партии заказа, т. е. время между включениями в работу первого станка (ед. времени);
• 4) h0 — точка заказа, т. е. размер запаса, при котором надо подавать заказ на производство очередной партии (ед. товаров).

Изменение уровня запасов происходит следующим образом (рис. 4.6): в течение времени t, работают оба станка, т. е. продукция производится и потребляется одновременно, вследствие чего запас накапливается с интенсивностью (? — v); в течение времени t2 работает только второй станок, потребляя накопившийся запас с интенсивностью v.

Формулы модели экономичного размера партии выглядят следующим образом:

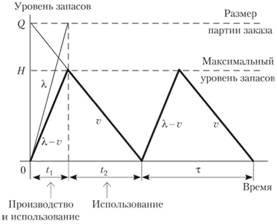
Рис. 4.6. График циклов изменения запасов.

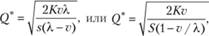
где Q* - величина оптимального заказа;

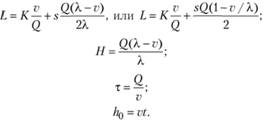
Пример. План годового выпуска продукции производственного предприятия составляет 1600 ед., при этом на каждую единицу готовой продукции требуется 1 ед. комплектующего изделия КИ-1. Известно, что стоимость подачи одного заказа составляет 200 руб., цена единицы комплектующего изделия — 480 руб., а стоимость содержания комплектующего изделия на складе составляет 15% его цены.

Определить оптимальный размер заказа на комплектующее изделие КИ-1.

Решение

Затраты на содержание запасов в определенный период складываются из следующих элементов:

• 1) суммарная стоимость подачи заказов;
• 2) цена заказываемого комплектующего изделия;
• 3) стоимость хранения запаса.

Оптимальный размер заказа соответствует минимальной величине совокупных издержек. Исходя из этого, для расчета оптимального размера заказа используется формула Уилсона. Формула Уилсона имеет следующий вид;

где Q — оптимальный размер заказа, шт.; A — затраты на поставку единицы заказываемого продукта, руб.; S — потребность в заказываемом продукте за определенный период, шт.; W — затраты на хранение единицы запаса, руб. / шт.

Используя формулу, определим оптимальный размер заказа, шт., по имеющимся исходным данным:

Округление оптимального размера заказа в большую сторону помогает избежать дефицита комплектующего изделия. Таким образом, оптимальный размер заказа составляет 95 шт.

Экономический анализ оперирует такими известными понятиями, как постоянные и переменные издержки, выручка от реализации, цена за единицу продукции, минимальный объем реализации (точка безубыточности), порог рентабельности, запас финансовой прочности, сила операционного (производственного) рычага.

Минимальный объем реализации (точка безубыточности) рассчитывается следующим образом:

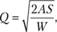
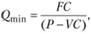
где FC — постоянные издержки; Р — цена единицы продукции; VC — переменные издержки на единицу продукции.

Перечисленные понятия используются для моделирования ситуаций типа: что будет с прибылью, если изменятся объем продаж, издержки, цена и др.

Определение точки безубыточности может проводиться графическим путем, как показано на рис. 4.7.

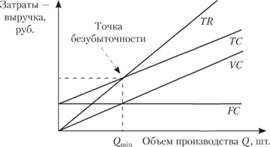
Рис. 4.7. График определения точки безубыточности.

Крутизна наклона кривой валовых поступлений зависит от цены товара. При увеличении фирмой цены товара наклон кривой валовых издержек становится более крутым, соответственно, фирма может сократить объем продаж, сохранив целевую прибыль Условие безубыточности имеет следующий вид:

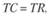
где ТС — общие издержки; TR — объем продаж;

отсюда.

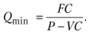
Следовательно, цена изделия в точке безубыточности может быть рассчитана следующим образом:

Предположим, что имеется фирма ио производству велосипедов. Стоимость одного изделия на рынке (Р) составляет 100 долл. Постоянные издержки (ГС) — 10 000 долл. Переменные издержки на единицу продукции (VС) — 10 долл. Тогда объем производства (Qmin), при котором общие издержки (ГС) полностью покрываются доходами (PQmin), составят 112 шт. (10 000/(100−10)).

Цена одного изделия при фиксированном объеме производства (Qmin = 50 шт.) составит 300 долл. (10 000 / 50 + 100).

Отсюда можно найти объем производства, при котором общие издержки полностью покрываются объемом продаж.

Варьируя величинами издержек и объемов продаж, можно добиться изменения положения точки безубыточности, например, если фирма стремится увеличить объем продаж при неизменном спросе. В этой ситуации прежде всего необходимо воздействовать на сам спрос, что приведет к увеличению расходов на рекламу, маркетинг и т. д. Необходимо также создавать ценовые преимущества, например путем снижения цен или предоставления дополнительных скидок. Соответственно, смещение точки безубыточности произойдет вправо.

Смещение точки безубыточности влево (т.е. приближение момента получения прибыли) возможно при сокращении издержек, в первую очередь постоянных.

Сложность метода состоит в том, что установление цены зависит от эластичности спроса по ценам, а график безубыточности этого не отражает. Поэтому фирма должна рассмотреть все возможные варианты установления цены, прежде чем прийти к окончательному решению.

Другие модели экономического анализа применяются для определения прибыли относительно инвестированного капитала, нахождения величины чистой прибыли, которую имеет в данный период фирма, и дивидендов на одну акцию внутри фирмы. Эти модели рассматриваются в дисциплинах по финансовому менеджменту и экономическому анализу.