Теорема Эрроу о невозможности

Многообразие процедур, пригодных для принятия коллективных решений, побуждает задуматься, есть ли среди них такие, которые идеальным образом соответствовали бы достаточно полному набору естественных требований (аксиом). Знакомство с теоремой Мэя и парадоксом Кондорсе заставляет скептически относиться к такой возможности. Генерализованный ответ на обсуждаемый вопрос дает теорема о невозможности, доказанная Кеннетом Эрроу^[1] в 1951 г.

Теорема утверждает, что не существует правила коллективного выбора у удовлетворяющего одновременно следующим шести требованиям.

• 1. Полнота. Правило должно обеспечивать выбор между любыми двумя альтернативами, отдавая предпочтение одной из них либо признавая обе равноценными.
• 2. Универсальность. Правило обеспечивает результативный выбор при любом сочетании индивидуальных предпочтений.
• 3. Транзитивность. Для любого набора из трех альтернатив х, у и z, если xRy и yRz, то xRz.
• 4. Единогласие. Если xRy выполняется для любого i, т. е. все участники коллективного выбора отдают предпочтение первой из двух альтернатив, то xRy, иначе говоря, коллективный выбор совершается в пользу первой альтернативы (это не что иное, как выполнение требования Парето-эффективности).
• 5. Независимость от посторонних альтернатив. Коллективный выбор между любыми двумя альтернативами х и у зависит от того, как индивиды оценивают эти две альтернативы по отношению друг к другу, но не зависит от отношения индивидов к какой бы то ни было посторонней альтернативе z (например, будет ли признано xRy, может зависеть, в частности, от того, верно ли, что хRiу, но не от того, справедливо ли, что xRz или что xRizRiy).
• 6. Отсутствие «диктатора». Среди участников коллективного выбора нет такого индивида, любое предпочтение которого xRiy влекло бы за собой xRy независимо от предпочтений всех других индивидов.

Теорему можно сформулировать и иным образом, введя важное понятие рационального выбора. Выбор является рациональным, если он отвечает требованиям полноты и транзитивности. Рациональность индивидуального выбора — одна из ключевых аксиом микроэкономики.

Коллективный выбор не всегда рационален, как мы убедились, рассматривая парадокс голосования. Теорема Эрроу говорит о том, что не существует правила рационального коллективного выбора, которое было бы универсальным, отвечало бы принципу эффективности по Парето, было бы независимо от посторонних альтернатив и при этом предполагало бы подлинно коллективное решение, не сводящееся к фиксации предпочтений одного индивида.

Приступая к доказательству теоремы, прежде всего введем понятие решающей коалиции голосующих. Решающей коалицией является такая совокупность индивидов, входящих в общее число участников коллективного выбора, что при единогласии внутри этой коалиции позиция ее членов становится результатом коллективного выбора. Иными словами, если для всех членов решающей коалиции xRty, то xRy. Коалиция может быть решающей только для конкретной пары альтернативных вариантов, тогда она называется решающей коалицией, например, для а против b. В то же время могут существовать коалиции, решающие для любой допустимой пары альтернатив; такие коалиции называют решающими без указания конкретной пары.

Докажем, что, если выполняются шесть перечисленных выше условий, то для произвольной пары альтернатив найдется решающая коалиция, состоящая из одного члена.

Выберем некоторую пару альтернатив х и у. Рассмотрим множество решающих для нее коалиций. Это множество не пусто, поскольку из аксиомы единогласия следует, что по крайней мере вся совокупность голосующих составляет решающую коалицию. Вместе с тем правило, удовлетворяющее шести аксиомам, не может быть правилом единогласного принятия решений, так как последнее не отвечает требованию универсальности. Всего лишь при двух участниках, если и 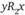(индексы обозначают номера голосующих), единогласное решение не может быть найдено. Следовательно, если существует правило, отвечающее всем шести требованиям, то найдется решающая коалиция для х против у с числом членов меньшим, чем общее число голосующих.

Выберем наименьшую по числу членов решающую коалицию для х против у и обозначим ее Т. Т включает хотя бы двух индивидов (в противном случае это решающая коалиция для х и у, состоящая только из одного члена). Разделим Т на две подгруппы. Пусть в первую из них (назовем ее D) входит один голосующий, а во вторую (V) — остальные члены наименьшей решающей коалиции для х против у (их может быть один или больше). Совокупность голосующих, не относящихся к T, обозначим W. Поскольку речь не идет о правиле единогласного принятия решений, W не пусто.

Возьмем любую третью альтернативу z. В силу универсальности найдется такой профиль предпочтений, что:

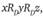(4.1).

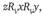(4.2).

(4.3).

где - нестрогие предпочтения всех членов подгрупп D, V и W.

Поскольку подгруппы D и V вместе составляют решающую коалицию для х против у, то из (4.1) и (4.2) следует xRy.

В то же время V не является решающей коалицией (иначе она была бы решающей в том числе для х и у). Поскольку х, у и z выбираются произвольно, то V, не будучи решающей коалицией, не окажется решающей и для всех возможных z против у. Следовательно, выбор V между z и у блокируется выбором D и W. Значит, из (4.1) и (4.3) вытекает, что невозможно zRy. Таким образом, получаем yRz.

В силу транзитивности: xRz. Однако согласно (4.2) и (4.3) из всех участников голосования только D может строго предпочитать альтернативу х альтернативе z. Получается, что выбор D, а это один человек, определяет общее решение, несмотря на противостояние всех остальных голосующих. Значит, по крайней мере в отношении альтернатив х и z (а они выбраны произвольно) существует «диктатор» .

Докажем теперь, что коалиция D, состоящая из одного члена, является решающей для любой пары альтернатив а и b, если эта коалиция — решающая для некоторой пары x и z.

Теперь W будет обозначать совокупность всех участников коллективного выбора, кроме единственного голосующего D, который выступает в роли решающей коалиции для х против z.

Возьмем любую альтернативу а и рассмотрим ситуацию, когда:

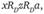(4.4).

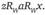(4.5).

Такие предпочтения найдутся в силу полноты и универсальности.

Поскольку D — решающая коалиция для х против z, то xRz. В силу аксиомы единогласия zRa. Поскольку предпочтения транзитивны, xRa.

Из аксиомы независимости от посторонних альтернатив следует, что, если исключить из (4.4) и (4.5) предпочтения, затрагивающие z, последний вывод не изменится. Таким образом, пр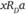и и 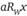всегда имеет место xRa. Но это означает, что D — решающая коалиция для х против любого а.

Теперь возьмем произвольную альтернативу Ь. Рассмотрим ситуацию, когда:

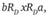(4.6).

(4.7).

По аналогии с предыдущим рассуждением, bRa, и, следовательно, D — решающая коалиция для b против а. Между тем в роли b и а могут выступать любые альтернативы. Итак, при рассмотрении всякой пары альтернатив исход коллективного выбора совпадает с выбором, который делает коалиция D, состоящая из одного члена. Теорема доказана.

Теорема о невозможности дает на первый взгляд неожиданный ответ на вопрос о перспективах демократического решения проблем, возникающих в обществе. В действительности этот ответ, с одной стороны, достаточно тесно связан с тем, что обсуждалось нами ранее, а с другой — вовсе не означает бесперспективности всякого демократического устройства политической жизни. Принципиальное значение теоремы Эрроу состоит как раз в том, что она обрисовывает ключевые предпосылки осуществимости (или неосуществимости) рационального демократического выбора.

Обратим внимание, что в числе аксиом, сформулированных в данном параграфе, находятся аксиомы полноты, единогласия и универсальности. Это значит, что условия теоремы допускают выбор между всевозможными Парето-эффективными состояниями при самых разных профилях предпочтений. Однако мы знаем, что такого рода выбор предполагает улучшение положения одних индивидов за счет других. Он влечет за собой непримиримые конфликты, и, как мы видели применительно к правилу простого большинства, провоцирует формирование неустойчивых коалиций. Теорема Эрроу говорит, в частности, о том, что в подобных ситуациях полностью гарантировать устойчивость (транзитивность) выбора удается лишь ценой отказа от его коллективного характера, иначе говоря, за счет появления «диктатора» .

На деле ослабить значимость проблемы, о которой идет речь, помогают конституционные ограничения вариантов перераспределения. Это очевидным образом сокращает набор альтернатив, из которых может делаться коллективный выбор, т. е. означает отказ от требования полноты.

Успеху коллективного выбора способствует также формирование сообществ на базе предпочтений, разделяемых всеми членами. Таковы, например, клубы, политические партии и т. д. Применительно к ним незначима аксиома универсальности. Принятие устойчивых коллективных решений в сообществах, члены которых разделяют общие ценности, гораздо более достижимо, чем в произвольных группах индивидов.

Аксиома независимости от посторонних альтернатив тесно связана с отказом от учета интенсивности индивидуальных предпочтений. Уместность такого отказа может показаться весьма сомнительной, и, например, правило Борда отражает интенсивность, а применение этого правила не ведет к циклическому голосованию. Проблема, однако, в том, что одновременный учет интенсивности предпочтений многих индивидов предполагает сравнение и соизмерение присущих каждому из них «шкал» полезности. То же правило Борда, по существу, есть способ суммирования интенсивностей индивидуальных предпочтений.

Между тем межличностная сопоставимость шкал полезности представляет собой весьма сильное предположение. Во всяком случае, сопоставление немыслимо без некоторых допущений об относительной значимости благосостояния разных индивидов для общества. Эти допущения, в принципе, могут основываться на консенсусе, предпочтениях большинства и т. д. Однако в таком случае они сами есть продукты коллективного выбора, а мы обсуждаем здесь его исходные условия. Вместе с тем на практике демократии не обходятся без неких явно или неявно фиксируемых представлений о значимости позиций отдельных индивидов. Например, влияние интенсивности предпочтений по отношению к кандидатам на выборные посты неодинаково сказывается при наличии или отсутствии первичных внутрипартийных выборов (того, что в США называется праймериз). В конечном счете теорема Эрроу позволяет понять, почему при наличии разнонаправленных интересов никакой вариант демократического устройства не гарантирует достижения идеала в сфере общественного выбора. Однако отсутствие демократии означало бы отсутствие коллективного выбора, как такового. Вместе с тем, при полном совпадении интересов граждан государство с его принуждающей силой не требовалось бы. В последующих параграфах этой главы нам предстоит рассмотреть, как реальные интересы действующих индивидов детерминируют политические процессы в условиях демократии.

• [1] Эрроу К. Д. Коллективный выбор и индивидуальные ценности. M.: ИД ГУ ВШЭ, 2004.