Метод максимального правдоподобия

Метод максимального правдоподобия (ММП) является одним из наиболее широко используемых методов в статистике и эконометрике. Для его применения необходимо знание закона распределения исследуемой случайной величины.

Пусть имеется некоторая случайная величина У с заданным законом распределения ДУ). Параметры этого закона неизвестны и их нужно найти. В общем случае величину Y рассматривают как многомерную, т. е. состоящую из нескольких одномерных величин У1, У2, У3 …, У.

Предположим, что У — одномерная случайная величина и ее отдельные значения являются числами. Каждое из них (У], у2, у3, …, у") рассматривается как реализация не одной случайной величины У, а ? случайных величин У1; У2, У3 …, У". То есть:

уj — реализация случайной величины У];

у2 — реализация случайной величины У2;

уз — реализация случайной величины У3;

у" - реализация случайной величины У".

Параметры закона распределения вектора У, состоящего из случайных величин Yb Y2, У3, У", представляют как вектор ?, состоящий из к параметров: ??, ?2,вк. Величины ?? ?2, У3,…, ?? могут быть распределены как с одинаковыми параметрами, так и с различными; некоторые параметры могут совпадать, а другие различаться. Конкретный ответ на этот вопрос зависит от той задачи, которую решает исследователь.

Например, если стоит задача определения параметров закона распределения случайной величины У, реализацией которой являются величины У1; У2, У3, У," то предполагают, что каждая из этих величин распределена так же, как величина У. Иначе говоря, любая величина У,• описывается одним и тем же законом распределения/(У,•), причем с одними и теми же параметрами ?: ??, ?2,…, дк.

Другой пример — нахождение параметров уравнения регрессии. В этом случае каждая величина У, рассматривается как случайная величина, имеющая «собственные» параметры распределения, которые могут частично совпадать с параметрами распределения других случайных величин, а могут и полностью различаться. Более подробно применение ММП для нахождения параметров уравнения регрессии будет рассмотрено ниже.

В рамках метода максимального правдоподобия совокупность имеющихся значений У], у2, у3, …, у" рассматривается как некоторая фиксированная, неизменная. То есть закон /(У;) есть функция от заданной величиныу, и неизвестных параметров ?. Следовательно, для п наблюдений случайной величины У имеется п законов /(У;).

Неизвестные параметры этих законов распределения рассматриваются как случайные величины. Они могут меняться, однако приданном наборе значений Уі, у2, у3, …, у" наиболее вероятны конкретные значения параметров. Иначе говоря, вопрос ставится таким образом: каковы должны быть параметры ?, чтобы значения уj, у2, у3, …, у" были наиболее вероятны?

Для ответа на него нужно найти закон совместного распределения случайных величин У1; У2, У3,…, Уп -КУі, У2, Уз, У"). Если предположить, что наблюдаемые нами величиныу^ у2, у3, …, у" независимы, то он равен произведению п законов/.

(У;) (произведению вероятностей появления данных значений для дискретных случайных величин или произведению плотностей распределения для непрерывных случайных величин):

или.

Чтобы подчеркнуть тот факт, что в качестве переменных рассматриваются искомые параметры ?, введем в обозначение закона распределения еще один аргумент — вектор параметров ?:

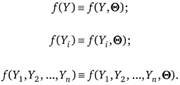
С учетом введенных обозначений закон совместного распределения независимых величин 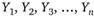с параметрами будет записан в виде.

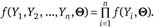(2.51).

Полученную функцию (2.51) называют функцией максимального правдоподобия и обозначают :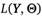

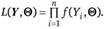
Еще раз подчеркнем тот факт, что в функции максимального правдоподобия значения У считаются фиксированными, а переменными являются параметры вектора (в частном случае — один параметр). Часто для упрощения процесса нахождения неизвестных параметров функцию правдоподобия логарифмируют, получая логарифмическую функцию правдоподобия

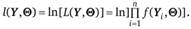
Дальнейшее решение по ММП предполагает нахождение таких значений ?, при которых функция правдоподобия (или ее логарифм) достигает максимума. Найденные значения ?; называют оценкой максимального правдоподобия.

Методы нахождения оценки максимального правдоподобия достаточно разнообразны. В простейшем случае функция правдоподобия является непрерывно дифференцируемой и имеет максимум в точке, для которой.

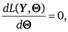
или.

В более сложных случаях максимум функции максимального правдоподобия не может быть найден путем дифференцирования и решения уравнения правдоподобия, что требует поиска других алгоритмов его нахождения, в том числе итеративных.

Оценки параметров, полученные с использованием ММП, являются:

• — состоятельными, т. е. с увеличением объема наблюдений разница между оценкой и фактическим значением параметра приближается к нулю;
• — инвариантными: если получена оценка параметра ?, равная 0L, и имеется непрерывная функция q (0), то оценкой значения этой функции будет величина q (0L). В частности, если с помощью ММП мы оценили величину дисперсии какого-либо показателя (af), то корень из полученной оценки будет оценкой среднего квадратического отклонения (?,), полученной по ММП.
• — асимптотически эффективными;
• — асимптотически нормально распределенными.

Последние два утверждения означают, что оценки параметров, полученные по ММП, проявляют свойства эффективности и нормальности при бесконечно большом увеличении объема выборки.

Для нахождения параметров множественной линейной регрессии вида.

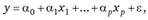
необходимо знать законы распределения зависимых переменных 7; или случайных остатков ?,. Пусть переменная Yt распределена по нормальному закону с параметрами ?,•, ?,•. Каждое наблюдаемое значение у, имеет, в соответствии с определением регрессии, математическое ожидание ?,• = МУ" равное его теоретическому значению при условии, что известны значения параметров регрессии в генеральной совокупности.

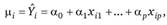
где xfl, …, xip — значения независимых переменных в і-м наблюдении. При выполнении предпосылок применения МНК (предпосылок построения классической нормальной линейной модели), случайные величины У, имеют одинаковую дисперсию.

Дисперсия величины определяется по формуле.

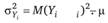
Преобразуем эту формулу:

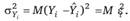(2.52).

При выполнении условий Гаусса — Маркова о равенстве нулю математического ожидания случайных остатков и постоянстве их дисперсий можно перейти от формулы (2.52) к формуле.

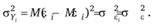
Иначе говоря, дисперсии случайной величины У, — и соответствующих ей случайных остатков совпадают.

Выборочную оценку математического ожидания случайной величины Yj будем обозначать.

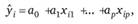
а оценку ее дисперсии (постоянной для разных наблюдений) как Sy.

Если предположить независимость отдельных наблюдений yit то получим функцию максимального правдоподобия.

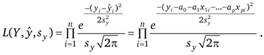(2.53).

В приведенной функции делитель 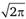является константой и не оказывает влияния на нахождение ее максимума. Поэтому для упрощения расчетов он может быть опущен. С учетом этого замечания и после логарифмирования функция (2.53) примет вид.

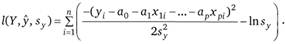
В соответствии с ММП найдем производные логарифмической функции правдоподобия по неизвестным параметрам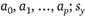

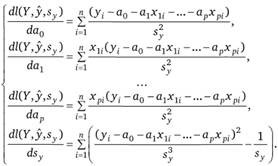
Для нахождения экстремума приравняем полученные выражения к нулю. После преобразований получим систему.

(2.54).

Эта система соответствует системе, полученной по методу наименьших квадратов. То есть ММП и МНК дают одинаковые результаты, если соблюдаются предпосылки МНК. Последнее выражение в системе (2.54) дает оценку дисперсии случайной переменной 7, или, что одно и то же, дисперсии случайных остатков. Как было отмечено выше (см. формулу (2.23)), несмещенная оценка дисперсии случайных остатков равна.

Аналогичная оценка, полученная с применением ММП (как следует из системы (2.54)), вычисляется по формуле.

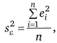
т.е. является смещенной.

Мы рассмотрели случай применения ММП для нахождения параметров линейной множественной регрессии при условии, что величина У, нормально распределена. Другой подход к нахождению параметров той же регрессии заключается в построении функции максимального правдоподобия для случайных остатков ?,. Для них также предполагается нормальное распределение с параметрами (0, ??). Нетрудно убедиться, что результаты решения в этом случае совпадут с результатами, полученными выше.