Расчет точного распределения совокупного ущерба в индивидуальных моделях методом свертки (композиции)

В индивидуальных моделях страховые выплаты, производимые страховой компанией, представляются как сумма выплат многим отдельным лицам. В большинстве случаев страховые выплаты отдельным лицам предполагаются независимыми. Поскольку суммарные выплаты Z представляют собой сумму независимых случайных величин, распределение случайной величины Z может быть определено с помощью классических теорем и методов теории вероятностей — использования свертки (композиции) случайных величин^[1].

Непрерывные случайные величины

Если Х1 и Х2 две независимые случайные величины с функциями распределения FjCxj) и Е2(.г2), то функция и плотность распределения величины Z = Xt + Х2:

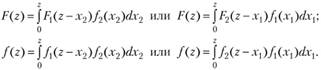
Применяя формулу свертки несколько раз, можно подсчитать функцию распределения или плотности любого количества слагаемых случайных величин.

Дискретные случайные величины

Если Хх и Х2 — независимые дискретные случайные величины, причем, как правило, целочисленные (выплаты в страховании либо являются целочисленными величинами, либо их можно представить такими), то работают с их законами распределения вероятностей:

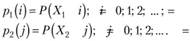
Чтобы найти закон распределения суммы 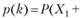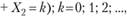необходимо просуммировать вероятности всех возможных вариантов, когда случайные величины Х{ и Х2 дают в сумме нужное значение:

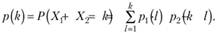(3.1).

ПРИМЕР 3.1

Портфель состоит из трех независимых однотипных договоров страхования неких крупных объектов, учитывающих:

• — гибель всего объекта, возможную с вероятностью 0,05 и при которой выплаты составляют 2 000 000 у.е.;
• — разрушение главного агрегата объекта, вероятность которого оценивают как 0,1 и выплаты равны 1 000 000 у.е.

Требуется найти:

• а) точное распределение суммарного ущерба по портфелю, используя метод сверток;
• б) размер рисковой премии, собираемой, но такому портфелю и обеспечиваемую собранной суммой вероятность неразорения страховой компании;
• в) суммарную рисковую надбавку, необходимую чтобы достичь вероятности неразорения 0,95.

Решение

Итак, распределение ущерба по каждому из трех договоров имеет вид:

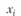		1 000 000 у.е.	2 000 000 у.е.
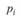	0,85.	0,1.	0,05.

Для сокращения и удобства записи распределений введем обозначение одной единицы страховой суммы 1 ЕСС = 1 000 000 у.е. Тогда распределение ущерба (в ЕСС) примет простой целочисленный вид:

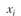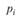	0,85.	0,1.	0,05.

а) Для подсчета суммы трех случайных величин — составления закона распределения суммарного ущерба по портфелю — последовательно сложим сначала первые две случайные величины, а затем к полученному распределению прибавим третью случайную величину — ущерб по третьему договору страхования.

Для суммирования Х{ и Х2 — свертки последовательностей /?,(/) и p->(j) запишем матрицу совместного распределения Xj и Х2, каждый элемент которой представляет собой вероятность совместного наступления событий 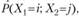которая, вследствие независимости случайных величин, равна произведению вероятностей:

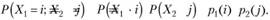
Для удобства расчета слева укажем столбец из вероятностей Pi (i), а сверху — строку из вероятностей p2(j)'•

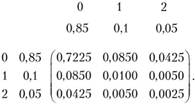
Для распределения ущерба по двум договорам страхования X, и Х2 получаем:

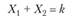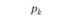	0,7225.	0,17.	0,095.	0,01.	0,0025.

Например, по (3.1) для суммарного ущерба, равного 0, 1, 2:

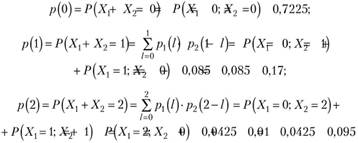и т. д.

Как видно, суммируются вероятности, параллельные главной диагонали матрицы совместного распределения вероятностей.

Для распределения суммарного ущерба по портфелю 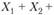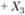необходимо к только что построенному распределению прибавить третью случайную величину 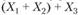. Для этого сначала образуем матрицу их совместного распределения из трех строк и шести столбцов:

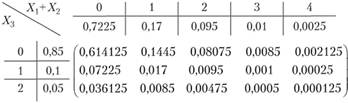
и в итоге получаем аналогично предыдущему этапу по (3.1) искомое точное распределение суммарного ущерба по портфелю из трех одинаковых договоров.

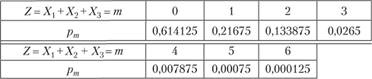
б) Размер суммарной рисковой премии будет равен математическому ожиданию ущерба по портфелю:

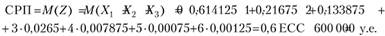
А еще проще воспользоваться свойством математического ожидания суммы независимых случайных величин:

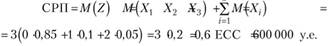
Рисковая премия на один договор: РП = M (Xj) = 0,2 ЕСС = = 200 000 у.е.

Собранной суммарной рисковой премии не хватит даже на 1 ЕСС выплат, поэтому страховая компания не разорится только в том случае, если выплат не будет вообще.

Вероятность неразорения (1 — ?) = P (Z = 0) = 0,614 125.

в) Чтобы определить, какую суммарную рисковую надбавку необходимо собирать, чтобы достичь вероятности неразорения 0,95, добавим к построенному распределению накопленные вероятности — функцию распределения случайной величины Z:

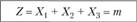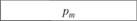	0,614 125.	0,21 675.	0,133 875.	0,0265.
Рт накопл.	0,614 125.	0,830 875.	0,96 475.	0,99 125.
Рт	0,7 875.	0,75.	0,125.
Рт накопл.	0,999 125.	0,999 875.

Мы видим, что с вероятностью 0,96 475 > 0,95 выплаты в портфеле договоров не будут превышать 2 ЕСС. Значит, суммарная рисковая надбавка должна покрывать все убытки, превышающие математическое ожидание ущерба — суммарную рисковую премию:

или по PH = 0,4(6) ЕСС = 466 667 у.е. на один договор.

Относительная рисковая надбавка составит 0 = 2,333 = 233,3%.

Такая огромная рисковая надбавка обусловлена тем, что у нас всего три договора с очень большой дисперсией риска.

Необходимость свертки возникает в малых по объему портфелях, когда нормальная аппроксимация неприменима. Например, при страховании космических и энергетических рисков, крупных промышленных объектов и т. п. — когда договоров немного, объекты имеют чрезвычайно высокую стоимость и важно знать точное распределение ущерба по всему портфелю. Часто такие портфели бывают неоднородными по составу.

Рассмотрим для примера такой неоднородный портфель с разными договорами.

ПРИМЕР 3.2

Портфель состоит из трех независимых договоров страхования неких крупных объектов, учитывающих:

• — гибель всего объекта;
• — разрушение главного агрегата объекта.

Вероятности этих событий и выплаты при этом составляют:

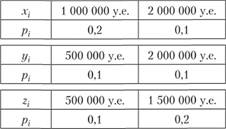
Необходимо найти:

• а) точное распределение суммарного ущерба по портфелю X + + Y + Z, используя метод сверток;
• б) размер суммарной рисковой премии, собираемой по такому портфелю, и обеспечиваемую собранной суммой вероятность неразорения страховой компании;
• в) размер рисковой надбавки, обеспечивающей вероятность неразорения, равную 0,98;
• г) сколько денежных средств необходимо иметь страховой компании в собственных активах, если при заданной в пункте в) надежности относительная рисковая надбавка не должна превышать 15%.

Решение

Портфель состоит из трех разных договоров страхования, но алгоритм построения распределения суммарного ущерба абсолютно такой же, как в примере 3.1. Для сокращения и удобства записи распределений введем обозначение одной единицы страховой суммы 1 ЕСС = 500 000 у.е. Тогда распределение ущерба по всем трем договорам примет простой целочисленный вид:

а) Для подсчета суммы трех случайных величин — составления закона распределения суммарного ущерба по портфелю — последовательно сложим сначала первые две случайные величины, а затем к полученному распределению прибавим третью случайную величину — ущерб по третьему договору страхования.

Алгоритм решения абсолютно аналогичен примеру 3.1, приведем краткое описание решения с основными результатами. Совместное распределение (X; У) имеет вид:

Суммарный ущерб по договорам X + Y имеет вид (3.1):

Для распределения искомого суммарного ущерба по портфелю X + У + Z необходимо к только что построенному распределению прибавить третью случайную величину Z. Для этого сначала образуем матрицу их совместного распределения:

В итоге получаем аналогично предыдущему этапу по (3.1) искомое точное распределение суммарного ущерба по портфелю из трех разных договоров:

б) Размер суммарной рисковой премии будет равен математическому ожиданию ущерба по портфелю:

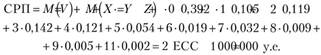
А еще проще воспользоваться свойством математического ожидания суммы независимых случайных величин:

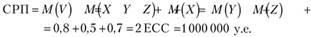
Собранной суммарной рисковой премии хватит на 2 ЕСС выплат, поэтому для нахождения обеспечиваемой ею вероятности неразорения страховщика построим функцию распределения суммарного ущерба по портфелю:

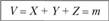Рт	0,392.	0,105.	0,119.	0,142.	0,121.	0,054.
Рт накопл.	0,392.	0,497.	0,616.	0,758.	0,879.	0,933.
Pm	0,019.	0,032.	0,009.	0,005.	0,002.
Рт накопл.	0,952.	0,984.	0,993.	0,998.

Если страховая компания будет собирать только рисковую премию, она не разорится с вероятностью: (1 — ?) = Р (V< 2) = 0,616.

в) Чтобы определить, какую суммарную рисковую надбавку необходимо собрать, чтобы достичь вероятности неразорения 0,98, посмотрим в предыдущей таблице функции распределения, где достигается накопленная вероятность 0,98.

Мы видим, что с вероятностью 0,984 > 0,98 выплаты в портфеле договоров не будут превышать 7 ЕСС: P (V < 7) = 0,984. Значит, суммарная рисковая надбавка должна покрывать все убытки, превышающие математическое ожидание ущерба — суммарную рисковую премию:

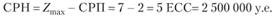
Относительная рисковая надбавка составит? = 2,5 = 250%.

Столь большая рисковая надбавка обусловлена тем, что у нас всего три договора с очень большой дисперсией риска.

г) Чтобы определить, сколько денежных средств необходимо иметь страховой компании в собственных активах, если при заданной в пункте в) надежности относительная рисковая надбавка не должна превышать 15%, определим, чему тогда должна быть равна суммарная рисковая надбавка:

Тогда для обеспечения надежности 1 —? = 0,98 страховой компании необходимо иметь следующее количество собственных средств:

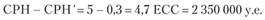
Это очень большая сумма, поэтому страховой компании более разумно перестраховать такие крупные риски (см. гл. 5) и назначить, если это возможно, более высокую рисковую надбавку.

• [1] Феллер В. Введение в теорию вероятностей и ее приложения. М.: ЛИБРОКОМ, 2010; Вентцель E. С. Указ, соч.; Фалин Г. И., Фалин А. И. Указ. соч.