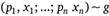Аксиомы потребительского выбора в условиях неопределенности

До сих пор мы предполагали, что индивиды (агенты) всегда действуют в условиях определенности: они знают цены всех товаров и знают, что любой доступный набор товаров может гарантированно быть получен. В реальном мире такие идеальные условия выполняются не всегда. Например, покупая автомобиль, потребитель должен учитывать будущую цену бензина, расходы на ремонт и цену, по которой он сможет через несколько лет автомобиль перепродать. Ничего этого в момент принятия решения он с уверенностью не знает. В подобных случаях присутствует неопределенность относительно результатов сделанного выбора. Хотя индивид может знать вероятность возможных исходов, окончательный исход остается неизвестным, пока он не реализуется.

КЕЙС

Главные экономические решения человека, в которых важную роль играет риск, касаются использования имеющихся у него возможностей: какой профессией заниматься, в какой предпринимательской деятельности участвовать, как инвестировать капитал (не в чем). Альтернативные использования возможностей могут быть классифицированы по трем широким группам в соответствии со степенью предполагаемого риска:

a) возможности, предполагающие небольшой риск или никакого риска в получении денежного дохода, — профессии вроде учительской, другие гражданские профессии, конторская работа; деловые предприятия типового, предсказуемого образца, такие, как многие предприятия общественного пользования; ценные бумаги, такие, как правительственные облигации, промышленные облигации высокого класса; некоторая недвижимость, особенно жилье, находящееся в частном владении;

b) возможности, предполагающие среднюю степень риска, но вряд ли приводящие к очень большой прибыли или к очень большим убыткам — профессии, такие, как у зубного врача, бухгалтера, некоторые виды административной работы, деловые предприятия обычного топа, в которых, однако, присутствует конкуренция, достаточная, чтобы сделать результат совершенно неизвестным; ценные бумаги, такие, как облигации низкого класса, привилегированные акции, обыкновенные акции высокого класса;

c) возможности, предполагающие большой риск, с некоторой вероятностью очень большой прибыли и с некоторой вероятностью очень больших убытков — профессии, предполагающие физический риск, такие, как пилотирование воздушных судов, автомобильные гонки, или такие профессии, как медицина и право; деловые предприятия в неиспытанных областях; ценные бумаги, такие, как сильно спекулятивные акции; некоторые виды недвижимости. Самым важным общим правилом в литературе о выборе среди этих трех возможностей является то, что, при прочих равных условиях использование (а) или © имеет в общем тенденцию быть предпочитаемым по сравнению с (Ь), т. е. людям, в общем, надо что-то платить, чтобы заставить их пойти на умеренный риск вместо того, чтобы подвергнуть себя малому или большому риску. Так, Маршалл говорит: «Существует много людей с твердым, уравновешенным характером, которые скорее предпочтут место, сулящее твердый доход, скажем 400 ф. ст. в год, чем место, которое не исключает возможности получения дохода в 600 ф. ст., но имеет те же шансы обеспечить лишь 200 ф. ст. Поэтому неопределенность, если она взывает к большим амбициям и возвышенным устремлениям, обладает особой привлекательностью лишь для очень немногих, но вместе с тем выступает как сдерживающее начало для многих из тех, кто делает выбор своей карьеры. Как правило, в расчете на равный доход уверенность в умеренном успехе более привлекательна, чем ожидание неопределенного успеха» .

Фридмен M., Сэвидж Л. Дж. Анализ полезности при выборе среди альтернатив, предполагающих риск // Вехи экономической мысли. Т. 1. Теория потребительского поведения и спроса / под ред. В. М. Гальперина. — СПб.: Экономическая школа, 1999. С. 215−216.

Объектами выбора в условиях неопределенности являются лотереи.

Пусть имеется два множества символов: множество 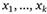и множество 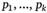. При этом символы - выигрыши некоторого индивида или потребительский набор, который он может получить; символы 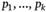- вероятности (при этом ).

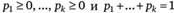Обозначим простую лотерею G, представляющую собой.

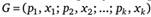
или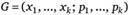

Символ 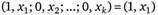представляет собой лотерею, в которой индивид выигрывает набор с вероятностью единица, т. е. получает набор 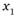наверняка, а символ 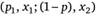означает лотерею, в которой индивид получает набор x1 с вероятностью р, а набор х2 — c вероятностью (?-p), где O? p?l.

Аналогично теории потребителя мы будем предполагать, что индивид имеет предпочтения? на множестве лотерей G. Отношение > (предпочтения — безразличия) удовлетворяют следующим аксиомам потребительского выбора в условиях неопределенности:

• 1) аксиома полноты — для любых двух лотерей G1 и G2 либо G1 >G2, либо G2? G1;
• 2) аксиома транзитивности. Для любых трех лотерей G1, G2 и G3, если G1? G2 и G2 > G3, то G1 > G3;
• 3) аксиома непрерывности. Для любых трех наборов х1, х2,х3, таких, что x1? х2 ?х3, существует вероятность Р, 0 < р < 1, для которой (p, х1; (1 — р), х3) ~ х2.

Это означает, что индивид не делает различий между лотереей (р, х1; (1 — р), х3), содержащей наиболее предпочтительный набор X1 и наименее предпочтительный набор X3, и определенностью набора х2, занимающего промежуточное положение между наборами x1 и х3;

4) аксиома монотонности. Для любых двух наборов X1 и х2, таких, что x1? x2, имеет место отношение предпочтения (P1, x1; (1 — p'), x2)? (p1, x1; (1 — p), x2) тогда и только тогда, когда р'>р.

Большинство людей предпочитают лотереи, приводящие к лучшим исходам с более высокой вероятностью, как того требует аксиома монотонности, однако это не всегда верно. Например, для любителей сафари гибель может быть наихудшим результатом охоты, но возможность погибнуть увеличивает удовольствие от нее. Охота с небольшой вероятностью гибели будет предпочитаться охоте с нулевой вероятностью гибели, что представляет собой явное нарушение монотонности;

5) аксиома замещения. Две лотереи эквивалентны для индивида, если для него эквивалентны их исходы и эти исходы реализуются с одинаковыми вероятностями. Если (pi, X1; (1-p'), х2)~ ~ (P1, X1; (1 — Р), х2), то р'~р.

Прежде чем формулировать следующую аксиому, дадим понятие сложной лотереи. Лотереи, в которых исходы сами являются лотереями, называются сложными (например, если в лотерее в качестве выигрыша выпадает лотерейный билет).

Например, предположим, что X = {х1, х2}. Рассмотрим сложную лотерею, которая с вероятностью p приводит к исходу x1, а с вероятностью (1 — р) дает лотерейный билет, который сам по себе является простой лотереей и приводит к исходу x1 с вероятностью р' и к исходух2 с вероятностью (1-р').

Исход x1 может возникнуть двумя взаимоисключающими способами: непосредственно как результат реализации первого исхода из множества X = {х1, х2} и опосредовано как результат реализации второго исхода-лотерейного билета. Вероятность получить x1 первым путем, очевидно, равна р. Вероятность получить его вторым путем равна (l-p)p', поскольку, чтобы прийти к нему через лотерейный билет, x1 должен быть результатом этого лотерейного билета, но не должен быть непосредственным итогом сложной лотереи. Таким образом, вероятность исходах, равна р + (1-р)р'. Аналогично эффективная вероятность исхода х2 составляет (1 — р) (1 — р');

6) аксиома о сведении сложной лотереи к простым. Если для любой лотереи является простой лотереей, порожденной g, то