Регрессионный анализ.

В результате изучения материала главы 4 обучающийся должен:

знать

• • основные понятия регрессионного анализа;
• • методы оценивания и свойства оценок метода наименьших квадратов;
• • основные правила проверки значимости и интервального оценивания уравнения и коэффициентов регрессии;

уметь

• • находить по выборочным данным оценки параметров двумерной и множественной моделей уравнений регрессии, анализировать их свойства;
• • проверять значимость уравнения и коэффициентов регрессии;
• • находить интервальные оценки значимых параметров;

владеть

• • навыками статистического оценивания параметров двумерного и множественного уравнения регрессии; навыками проверки адекватности регрессионных моделей;
• • навыками получения уравнения регрессии со всеми значимыми коэффициентами с использованием аналитического программного обеспечения.

Основные понятия

После проведения корреляционного анализа, когда выявлено наличие статистически значимых связей между переменными и оценена степень их тесноты, обычно переходят к математическому описанию вида зависимостей с использованием методов регрессионного анализа. С этой целью подбирают класс функций, связывающий результативный показатель у и аргументы «вычисляют оценки параметров уравнения связи и анализируют точность полученного уравнения [3, 13].

Функция |, описывающая зависимость условного среднего значения результативного признака у от заданных значений аргументов, называется уравнением регрессии.

Термин «регрессия» (от лат. regression — отступление, возврат к чемулибо) введен английским психологом и антропологом Ф. Гальтоном и связан с одним из его первых примеров, в котором Гальтон, обрабатывая статистические данные, связанные с вопросом о наследственности роста, нашел, что если рост отцов отклоняется от среднего роста всех отцов на х дюймов, то рост их сыновей отклоняется от среднего роста всех сыновей меньше, чем на x дюймов. Выявленная тенденция была названа регрессией к среднему состоянию.

Термин «регрессия» широко используется в статистической литературе, хотя во многих случаях он недостаточно точно характеризует статистическую зависимость.

Для точного описания уравнения регрессии необходимо знать условный закон распределения результативного показателя у. В статистической практике такую информацию получить обычно не удается, поэтому ограничиваются поиском подходящих аппроксимаций для функции f (xu х2,… л*), основанных на предварительном содержательном анализе явления или на исходных статистических данных.

В рамках отдельных модельных допущений о типе распределения вектора показателей < 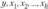) может быть получен общий вид уравнения регрессии 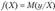, где . Например, в предположении о том, что исследуемая совокупность показателей подчиняется ()-мерному нормальному закону распределения с вектором математических ожиданий.

, где , и ковариационной матрицей ,.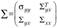

где  — дисперсия у,

• —  ковариация между величинами и.
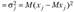• —  дисперсия

Уравнение регрессии (условное математическое ожидание) имеет вид

Таким образом, если многомерная случайная величина ()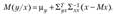

подчиняется ()-мерному нормальному закону распределения, то уравнение регрессии результативного показателя у по объясняющим переменным 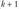имеет линейный по х вид.

Однако в статистической практике обычно приходится ограничиваться поиском подходящих аппроксимаций для неизвестной истинной функции регрессии f (x), так как исследователь не располагает точным знанием условного закона распределения вероятностей анализируемого результативного показателя у при заданных значениях аргументов х.

Рассмотрим взаимоотношение между истинной , модельной 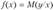и оценкой регрессии [1, 29]. Пусть результативный показатель у связан с аргументом х соотношением.

где 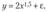 — случайная величина, имеющая нормальный закон распределения, причем и 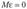. Истинная функция регрессии в этом случае имеет вид.

Предположим, что точный вид истинного уравнения регрессии нам неизвестен, но мы располагаем девятью наблюдениями над двумерной случайной величиной, связанной соотношением 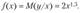и представленной на рис. 4.1.

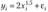
Рис. 4.1. Взаимное расположение истинной f (x) и теоретической уы модели регрессии.

Расположение точек на рис. 4.1 позволяет ограничиться классом линейных зависимостей вида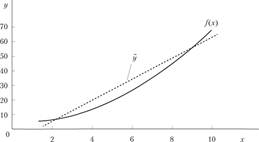

С помощью метода наименьших квадратов найдем оценку 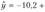уравнения регрессии.

Для сравнения на рис. 4.1 приводятся графики истинной функции регрессии и теоретической аппроксимирующей функции регрессии 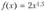. К последней сходится по вероятности оценка уравнения регрессии уы при неограниченном увеличении объема выборки ().

Поскольку мы вместо истинной функции регрессии ошибочно выбрали линейную функцию регрессии, что, к сожалению, достаточно часто встречается в практике статистических исследований, то наши статистические выводы и оценки не будут обладать свойством состоятельности, т. е. так бы мы ни увеличивали объем наблюдений, наша выборочная оценка не будет сходиться к истинной функции регрессии

Если бы мы правильно выбрали класс функций регрессии, то неточность в описании 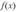с помощью уы объяснялась бы только ограниченностью выборки и, следовательно, она могла бы быть сделана сколько угодно малой при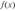

С целью наилучшего восстановления по исходным статистическим данным условного значения результативного показателя 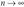и неизвестной функции регрессии 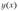наиболее часто используют следующие критерии адекватности функции потерь [29].

1. Метод наименьших квадратов, согласно которому минимизируется квадрат отклонения наблюдаемых значений результативного показателя , , от модельных значений , где 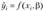коэффициенты уравнения регрессии;  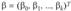— значения вектора аргументов в «-М наблюдении:

Решается задача отыскания оценки вектора . Получаемая регрессия называется средней квадратической.

2. Метод наименьших модулей, согласно которому минимизируется сумма абсолютных отклонений наблюдаемых значений результативного показателя от модульных значений 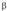, т. е.

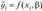
Получаемая регрессия называется среднеабсолютной (медианной).

3. Метод минимакса сводится к минимизации максимума модуля отклонения наблюдаемого значения результативного показателя у, от модельного значения 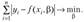, т. е.

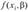
Получаемая при этом регрессия называется минимаксной.

В практических приложениях часто встречаются задачи, в которых изучается случайная величина у, зависящая от некоторого множества переменных и неизвестных параметров . Будем рассматривать (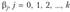) как (k + 1)-мерную генеральную совокупность, из которой взята случайная выборка объемом п, где () результат /-го наблюдения, . Требуется по результатам наблюдений оценить неизвестные параметры 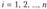. Описанная выше задача относится к задачам регрессионного анализа.

Регрессионным анализом называют метод статистического анализа зависимости случайной величины у от переменных 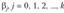, рассматриваемых в регрессионном анализе как неслучайные величины, независимо от истинного закона распределения

Часто предполагается, что случайная величина у имеет нормальный закон распределения с условным математическим ожиданием , являющимся функцией от аргументов , и постоянной, не зависящей от аргументов дисперсий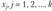

Следует помнить, что требование нормальности закона распределения у необходимо лишь для проверки значимости уравнения регрессии и его параметров , а также для интервального оценивания . Для получения точечных оценок 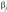, этого условия не требуется.

В регрессионном анализе под линейной моделью подразумевают модель, линейно зависящую от неизвестных параметров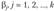

Простейшей линейной будем называть модель, линейно зависящую как от параметров , так и от переменных .

В общем виде линейная модель регрессии имеет вид.

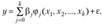
где - некоторая функция его переменных - случайная величина с нулевым математическим ожиданием и дисперсией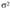

В регрессионном методе вид уравнения регрессии выбирают исходя из анализа физической сущности изучаемого явления и результатов наблюдения.

Наиболее часто встречаются следующие виды уравнений регрессии:

• • линейное множественное ;
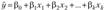• • полиномиальное ;
• • гиперболическое ;
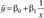• • степенное

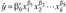
Путем логарифмирования степенные уравнения регрессии могут быть преобразованы в линейные уравнения относительно параметров 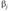. Логарифмируя, получим.

Пусть 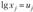для , тогда после подстановки будем иметь линейное уравнение регрессии: 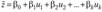В результате замен переменных 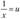и 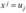гиперболическое и полиномиальное уравнения также могут быть преобразованы в линейные, теория которых разработана наиболее полно.

Оценки неизвестных параметров уравнения регрессии находят обычно методом наименьших квадратов. Ниже мы остановимся более подробно на этом методе и свойствах оценок, найденных этим методом.