Нули голоморфной функции. 
Теорема единственности

Здесь будет использована следующая терминология. Множество в метрическом пространстве называется изолированным, если каждая его точка имеет окрестность, в которой нет остальных точек множества. Например, двухточечное множество числовой прямой изолированное, множество рациональных чисел таким не является.

Расстояние между двумя множествами X, Y метрического пространства с метрикой р — это нижняя грань расстояний р{х, у), когда хеХ, a ye Y. Ниже нам понадобится такой факт: если X, Y — замкнутые множества комплексной плоскости и нс пересекаются, то расстояние между ними положительно.

Нулем комплекснозначной функции называется значение аргумента, при котором значение функции равно нулю. Множество всех нулей может иметь самую различную природу. Например, у многочлена конечное число нулей, нули sinz образуют счетное множество (какое?), функция z-z имеет своими нулями все действительные числа, а у функции l+|z|² множество нулей нусгое.

В действительном анализе нули дифференцируемых функций могут иметь предельные нулевые точки, в которых дифференцируемость сохраняется (но при этом множество всех нулей не является изолированным). Так, например, обстоит дело с функцией /(л) = х² sin —, неопределенной пока при.

х

х = 0. В действительном анализе се в этой точке доопределяют по непрерывности: полагают /(0) как предел функции при >0, т.с. равным 0. Множество нулей {0, — (к = ± 1,±2,…)} не является изолированным: у нуля л=0 /глист окрестности, свободной от других нулей. В комплексном анализе дело обстоит не так: нули голоморфной функции непременно изолированы, они могут иметь предельные точки лишь на границе области голоморфности. Убедимся в этом на примере функции f (z) = z² sin —. Ее изолированные нули.

Z

z_k =—, к eZ{0} имеют предельную точку z = 0, но в ней функция переплетает быть голоморфной, ибо при z-эО по некоторым направлениям (например, вдоль мнимой оси) функция стремится к бесконечности. Так, пола;

1 . е^ь-е~^ь

гая z_n =— (neN), в силу равенства sinz =- получим.

ni 2/.

1 «н -п 1C С

f (z_n) =—(—=?—=-), а первое слагаемое в скобках бесконечно большое.

2л п п

В курсе алгебры устанавливается, что многочлен P (z) обладает следующим свойством: если а — его корень (нуль), то найдется такое натуральное число к (оно называется кратностью нуля), что P (z) = (z — а)^к Q (z) > где Q (z) — многочлен, не обращающийся в нуль при z — a. Оказывается, что любая голоморфная (или, что-то же, аналитическая) функция обладает аналогичным свойством.

Теорема 11.1. Если точка а является нулем голоморфной в этой точке функции /(z), не равной тождественно нулю ни в какой окрестности а, то существует такое к eN, что.

где функция (p{z) голоморфна в точке а и отлична от нуля в некоторой окрестности этой точки.

Доказательство. В самом деле, в некоторой окрестности U точки а функция /(z) разлагается в ряд по степеням z-a с некоторыми коэффициентами с_п. Свободный член этого ряда равен нулю, ибо f (a) = 0. Пусть с_к — первый по порядку коэффициент, отличный от нуля, т.с. с₀ = с, = … = с_к__х = 0, с_к * 0. Тогда в U имеем.

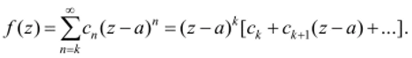
Для получения равенства (11.1) осталось сумму в квадратных скобках обозначить (p{z).

Теорема показывает, что голоморфная функция обращается в нуль как целая степень (z-a).

Число к из представления (11.1) называют кратностью (порядком) нуля а аналитической функции f (z). При к = 1 нуль простой, иначе — кратный. Формула (10.9) позволяет формулировать понятие кратности следующим образом: это номер младшей, отличной от нуля, производной f^{ka). Иными словами, точка а называется нулем голоморфной функции jz) порядка к, если.

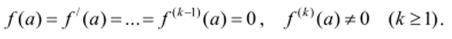
Пример 11.1. Число ^а~~^ является, как легко проверить, нулем функции f (z) = 1 + cos2z. Какова его кратность?

Решение. Имеем.

Ответ: кратность равна 2.

Подобно тому, как это делается для многочленов, можно определить порядок нуля при помощи делимости: он равен наивысшей степени (z-a)^k, на которую функция «делится» в том смысле, что частное.

после продолжения по непрерывности в точку а оказывается функцией, голоморфной в этой точке.

го порядка. Это видно из разложения.

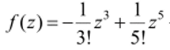
После деления обеих частей равенства на z³ справа получим функцию, голоморфную в точке 0 (и отличную от нуля в ней).

Перейдем далее ко второй части, указанной в заголовке данной главы, — теореме единственности. Она выражает одно из важнейших свойств голоморфных функций, у которого нет аналога в действительном анализе. Начнем со следующего утверждения.

Теорема 11.2. Пусть функция /(z) голоморфна в области DcC и обращается в нуль на бесконечном множестве? czD, имеющем предельную точку ае D. Тогда /(z) = 0 Vz е D.

Доказательство. Проведем его в два этапа.

1). Сначала покажем, что функция есть тождественный нуль в некоторой окрестности точки а. Используем «метод от противного». В круге К с центром а радиуса d, равного расстоянию от а до границы области до.

(рис. 17а)), представим функцию степенным рядом ^c"(z — а)" .

п=0.

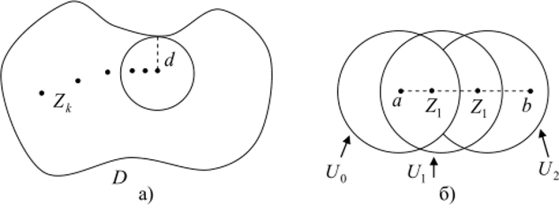
Рис. 17.

Среди коэффициентов разложения хотя бы один отличен от нуля. Среди ненулевых коэффициентов будет имеющий наименьший номер, обозначим его с_т. Тогда в степенном ряде суммирование начнется с номера т. Поэтому при z g К {а} выполняется равенство.

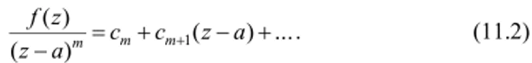
По условию точка а является предельной для Е, поэтому существует последовательность (z_k): z_k е ?, z_k —> a, z_k Ф а. Нс теряя общности, можно считать, что все такие точки лежат в К. Но f{z_k) = 0, поэтому из (11.2) получаем 0 = c_m+c_m+_l(z_k-a) + … В этом равенстве перейдем к пределу при к —>оо. Так как в стеленном ряде такой переход можно выполнить почленно, то получаем 0 = с_т вопреки предположению об этом коэффициенте.

2). Докажем далее, что если точка 6eD{a}, то f (b) = 0. Фиксируем такую точку и соединим ее с а ломаной L a D с конечным числом звеньев. Пусть d — расстояние между этой ломаной и границей dD области. Эти множества оба замкнутые, поэтому d>0. Возьмем число ре (0,d) и рассмотрим круг U_s = U (z_s, p) с центром в z_seL и радиусом р. Здесь индекс s пробегает значения 0,1,…,/? (neN), при этом z₍₎ = a, центр последующего круга лежит в предыдущем круге, а п подбирается так, что beU". На рис. 176) в целях обозримости ситуации ломаная состоит из одного звена (оно помечено пунктиром), п = 2. Этим частным случаем мы и ограничимся. Круг U₀ является частью указанного выше круга К, поэтому /(г) = 0 Vz е U₀. В частности, /(z) = 0 на бесконечном множестве U₀nU_l. Точка z, для него является предельной, поэтому, согласно пункту 1), функция есть тождественный нуль на (7,. Затем такая ситуация повторится увеличением индекса на 1. При п — 2 имеем: /(z) = 0 в U₂ => f (b) = 0, что и требовалось доказать.

Как следствие из теоремы 11.2 вытекает следующее утверждение, которое называют теоремой единственности или принципом единственности.

Если две функции f₂(z), голоморфные в области DaC, совпа

дают на множестве E (z) = /₂(z).

Эта теорема (также, как и многие другие) показывает существенное отличие понятия голоморфности функции в комплексном анализе от понятия дифференцируемости в смысле действительного анализа. В самом деле, две даже бесконечно дифференцируемые функции действительного переменного могут совпадать на части их общей области определения, нс совпадая тождественно. Рассмотрите, например, функции.

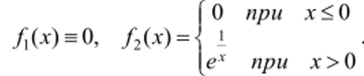
Но по теореме единственности две голоморфные функции, совпадающие на любом множестве с предельной точкой в области их голоморфности (например, на маленьком кружке или на дуге в области), совпадают тождественно во всей области.

Теорема единственности находит многочисленные применения. Например, основное тригонометрическое тождество cos² z + sin² z = 1 можно доказать с помощью формул Эйлера. Теорема единственности позволяет это сделать проще: слева и справа равенства стоят функции, голоморфные на всей комплексной плоскости, и для действительных значений аргумента они равны. Значит, они равны и на всей плоскости.

Заметим, что в теореме единственности условие, что предельная точка а есть внутренняя точка области, существенно: если оно нс выполняется, то тождественность функций утверждать нельзя. Например, функции.

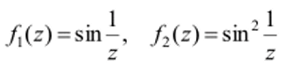
голоморфны в С {0}. Обе обращаются в нуль (и, следовательно, равны друг другу) в точках z_k =—(keZ, k* 0), но функции не тождественные. Здесь кл

теорема единственности неприменима, ибо z_k —> 0, но предел не является внутренней точкой области голоморфности функций.

Задачи к главе 11.

11.1. Определить порядок нуля функции.

• 11.2. Доказать, что функциональное уравнение f (z) = f (2z) нс имеет решений, голоморфных в точке z = 0 и отличных от тождественной постоянной.
• 11.3. Существует ли функция, голоморфная в круге z<2 и принимающая в точках z_n=— (п? N) значения п

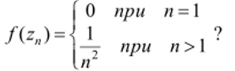
11.4. Существует ли функция, голоморфная в круге |г|<1, со свойст;

вом /(—) = —— при /7 = 2,3,???

/7 /7 + 1.

• 1
• 11.5. Функция е^г принимает значение 1 на бесконечном множестве точек, предельной точкой которого является z = 0. Но ведь эта функция не есть тождественная единица. Почему нет противоречия с теоремой единственности?

Ряды Тейлора хорошо приспособлены для представления голоморфных функций в кругах. Здесь мы рассмотрим более общие ряды по положительным и отрицательным степеням (z-я). Такие ряды (ряды Лорана^[1]) представляют голоморфные функции в кольцах вида.

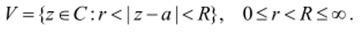
Особенно важны разложения в кольцах с нулевым внутренним радиусом, т.с. в проколотых окрестностях. Эти разложения позволяют изучать функции в окрестностях точек, где они теряют голоморфность (в особых точках).

Теорема 12.1 (теорема Лорана). Любую функцию, голоморфную в кольце V, можно в нем представить как сумму сходящегося ряда.

с коэффициентами.

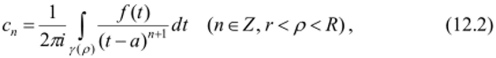
где у (р) — окружность с центром а радиуса р.

Доказательство. Фиксируем произвольно точку z е V и построим концентрическое кольцо V_t с радиусами t >/% /?,</?, содержащее z (сделайте чертеж). По интегральной формуле Коши для многосвязной области специального вида (в данном случае для кольца), указанного перед теоремой 9.2, имеем.

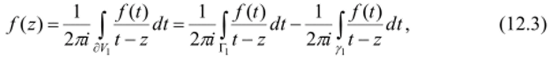
где окружности Г: | z — а |= Я,: | z — а |= г_{ ориентированы против часовой стрелки.

Для всех / е Г, имеем | -——1< q<, поэтому геометрический ряд t — а

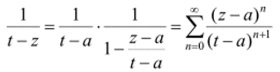
сходится абсолютно и равномерно по I на Г,. Умножая его на ограниченную функцию — /(/) (что не нарушает равномерной сходимости) и интегрируя 2т

почленно вдоль Г, получим.

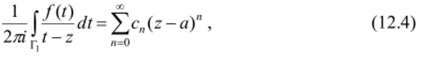
где.

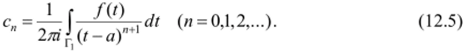
Второй интеграл в формуле (12.3) разлагается иначе. При всех имеем |—<1, поэтому получаем абсолютно и равномерно сходящий- z-a

ся на у, геометрический ряд:

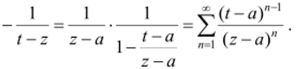
Снова, умножая обе части равенства на ограниченную функцию — /(/) и.

2 т

интегрируя почленно вдоль у, получаем.

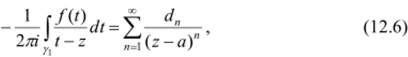
где.

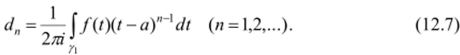
Заменим теперь в формулах (12.6), (12.7) индекс и, пробегающий значения 1,2, …, индексом -п со значениями -1, -2,…, и обозначим.

Тогда разложение (12.6) примет вид.

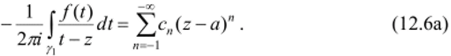
Теперь подставим (12.4) и (12.6а) в (12.3); получим нужное разложение (12.1), в котором ряд определен как объединение рядов (12.4) и (12.6а). Остается заметить, что функция /(/)(/ - я)" ^-1 при любом целом п голоморфна по teV, поэтому интегрирование по Г, и /, в формулах (12.5), (12.8) можно заменить интегрированием по любой окружности с центром а, лежащей в кольце V.

Теорема 12.1 доказана. П. Лоран опубликовал ес в 1843 г. Немного ранее она была получена К. Вейерштрассом, но была опубликована лишь в 1894 г.

Ряд (12.1), коэффициенты которого вычисляются по формулам (12.2), называется рядом Лорана функции f (z) в кольце V. Совокупность членов этого ряда с неотрицательными степенями называется его правильной частью, а совокупность членов с отрицательными степенями — главной частью (естественность названий выяснится далее). Как и в случае степенных рядов, имеет место теорема единственности разложения функции в данном кольце в ряд по положительным и отрицательным степеням. Приведем ее без доказательства (смотрите его, например, в работе [16, стр. 130−131]).

Теорема 12.2. Если функция f (z) в кольце V представима рядом вида (12.1), то коэффициенты этого ряда находятся по формулам (12.2).

Это утверждение часто формулируют так: всякий сходящийся ряд по положительным и отрицательным степеням (z-a) является рядом Лорана своей суммы.

Формулы (12.2) для коэффициентов ряда Лорана на практике применяются сравнительно редко, ибо они требуют вычисления интегралов. Обычно функцию /(z), голоморфную в кольце, стараются представить в виде суммы или произведения двух функций, из которых одна, например, f{z) голоморфна внутри большего круга, а другая, f₂(z), голоморфна во внешности замыкания меньшего круга. Первую разлагают по положительным степеням (z-a), вторую — по отрицательным, после чего ряды складывают или перемножают.

Пример 12.1. Функция.

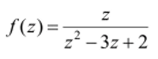
голоморфна везде, кроме точек z = l, z = 2. В кольце 1 < | z |< 2 ее требуется разложить в ряд Лорана.

2 1.

Решение. Разложим данную дробь на простейшие: /(z) =—-.

z-2 z-1.

Здесь первое слагаемое в круге |z|<2 разлагаем в ряд по положительным степеням z, привлекая геометрический ряд:

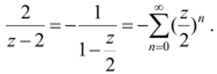
Дробь—— при | z | > 1 разложим по отрицательным степеням z, получим.

z-1.

се представление.

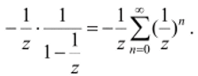
Ответ:

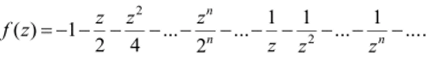
z-t—.

Пример 12.2. Разложить функцию f (z) = e ² в ряд по положительным и отрицательным степеням z.

Решение. При 0<|z|.

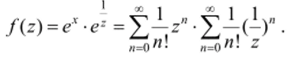
Осталось выполнить умножение рядов. Классики анализа (Эйлер, Ныотон и др.) в совершенстве владели соответствующей техникой. Читателю предлагаем убедиться (индукцией) в том, что после раскрытия скобок коэффициенты.

к 1.

а_к при z и а__к при — одинаковы и равны:

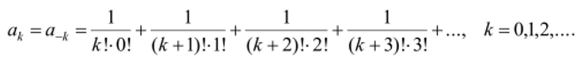
Далее мы рассмотрим точки, в которых нарушается голоморфность функций. Точка а е С называется изолированной особой точкой функции /(z), если существует се проколотая окрестность (т.с. множество {z:0<|z-tf |0}), в которой функция голоморфна. В зависимости от поведения функции при приближении аргумента к такой точке различают три типа особых точек.

Изолированная особая точка а функции /(z) называется:

1) устранимой точкой, если существует конечный предел.

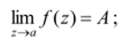
2) полюсом, если существует предел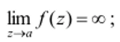

3) существенно особой точкой, если функция не имеет ни конечного, ни бесконечного предела при z-*a .

Все три тина изолированных особых точек реализуются. Например, у sin z.

функции/(г) = —- точка z = 0 является устранимой (докажите!). Функция.

z.

f (z) = z~ⁿ (n e N) имеет полюс в точке z = 0. У функции f (z) = e^: точка а = 0 является существенно особой. Например, при стремлении z = yi к нулю по мнимой оси функция /(z) = cos——I sin — предела не имеет.

У У

Могут, конечно, существовать и неизолированные особые точки. Например, функция.

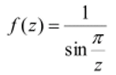
имеет полюсы в точках z = — (п = ± 1,±2,…), следовательно, z — О является.

/7.

для нее неизолированной особой точкой — предельной точкой полюсов. Более сложный пример особых точек доставляет функция.

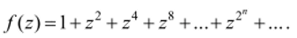
Оказывается, что каждая точка окружности |z|=l является для нее особой (смотрите об этом, например, источник [16, стр. 136]. Таким образом функция имеет целую линию, составленную из неизолированных особых точек.

Характер изолированной особой точки z = aeC тесно связан с характером лорановского разложения функции в проколотой окрестности этой точки (часто его коротко называют разложением в окрестности а). Эта связь выражается следующими тремя утверждениями, которые приводим без доказательств (их можно найти, например, в источнике [16] на страницах 137- 141).

Теорема 12.3. Изолированная особая точка аеС функции /(z) является устранимой в том, и только в том случае, если ее разложение в ряд Лорана в окрестности а не содержит главной части, т. е.

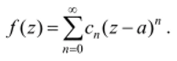
Теорема 12.3'. Изолированная особая точка я е С функции /(z) является устранимой в том, и только в том случае, если функция ограничена в проколотой окрестности точки а.

Продолжив функцию в се устранимую точку а по непрерывности, т.с. положив /(tf) = lim /(z), получим функцию, голоморфную в а (т.с. устра;

*->я ним особенность). Этим оправдывается термин «устранимая особенность». В литературе часто такие точки называют правильными или регулярными, а не особыми.

Теорема 12.4. Изолированная особая точка аеС функции /(z) является полюсом в том, и только в том случае, если главная часть лорановского разложения функции в окрестности точки а содержит лишь конечное (и положительное) число отличных от нуля членов:

Отметим простой факт о связи полюсов с нулями: точка а является полюсом функции /(z) в том и только том случае, если функция.

(p (z) = —-— не есть тождественный ноль, голоморфна в окрестности а и.

/(г).

(р{а) = 0. При этом порядком полюса функции /(z) называется порядок нуля «перевернутой» функции (p{z). Очевидно, порядок полюса совпадает с номером N старшего члена главной части лорановского разложении в проколотой окрестности полюса.

z²-l.

Например, пусть /(z) = ^—. Функция (p{z) имеет простые нули в z^+l.

точках z = ±/, являющимися полюсами (простыми) /(z). У функции.

/(z) = — ^Z+—полюсы г = 2лк (к е Z) двойные (почему?).

1-cosz.

Теорема 12.5. Изолированная особая точка аеС функции /(z) является существенно особой в том и только в том случае, если главная часть лорановского разложения функции в окрестности а содержит бесконечно много отличных от нуля членов.

Поведение функции в окрестности существенно особой точки описывает следующая теорема, которую в зарубежных учебниках приписывают Карлу Вейерштрассу, опубликовавшему ее в 1876 г. Между тем ее доказал Юлиан Васильевич Сохоцкий (1842−1927) еще в 1868 г. одновременно с итальянцем Ф.Казорати.

Теорема 12.6 (Теорема Сохоцкого). Если аеС является существенно особой точкой голоморфной функции /(z), то для любого числа АеС или символа Л =оо можно найти последовательность точек z_n—>a такую, что Смысл теоремы в том, что в окрестности существенно особой точки функция принимает значения, сколь угодно близкие к любому наперед заданному значению величины в С. Совокупность предельных значений функции по различным последовательностям z" —> а называют множеством неопределенности f (z) в точке а. Если она является устранимой или полюсом, то множество неопределенности состоит из одной точки (конечной или бесконечной). Теорема Сохоцкого утверждает, что для существенно особой точки реализуется другой крайний случай: множество неопределенности заполняет всю расширенную плоскость С .

Заметим, что в теореме Сохоцкого не доказывается, что уравнение J'(z) = c при любом с, конечном или бесконечном, имеет бесконечное множество корней (и_п):и" —> а. Утверждается только, что-либо существуют такие корни, либо существует последовательность точек z_n (л е N) со свойством f (z_n)->c. Пикар^[2] доказал более тонкую теорему: уравнение f (z) = c для любого значения се С, кроме, может быть, одного, имеет бесконечное множество корней, стремящихся к а.

Это утверждение формулируют также слежующим образом: в любой проколотой окрестности существенно особой точки функция принимает любое значение, кроме, может быть, одного. Например, функция f (z) = e^z в проколотой окрестности точки z = 0 принимает любое значение, кроме нуля. Доказательство теоремы Пикара очень сложное и обычно не приводится в стандартных курсах ТФКП. Здесь — также.

Пример 12.3. Проверить теорему Сохоцкого для функции f (z) = e^z. Решение. Единственной (изолированной) особой точкой является z = 0. Так как.

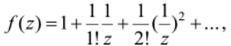
то эта точка существенно особая. Пусть задано комплексное число Л€С{0}. Найдем точки, в которых функция принимает данное значение. Таких точек бесконечно много:

Имеем: z" -> 0 (л е N), f (z_n) = А => lim f (z_n) = А .

rt-KO.

Рассмотрим случай А = 0. Последовательность с общим членом.

z_n -сходится к нулю и Jz_n) = е~^п —> 0 при п^>оо. п

Если А = оо, то берем z"=—>0 (neN). Тогда f{z_n) = eⁿ —>со мри.

п

п —>оо.

Итак, для любого // е С удается подобрать такую последовательность точек z_n —> 0, что /(z,) —>^, в чем и состоит утверждение теоремы Сохоцкого.

Заметим, что анализ особых точек функций комплексного переменного часто позволяет объяснить то, что в рамках действительного анализа остается неясным. Известен пример Коши функции.

Она везде в R имеет производные всех порядков (смотрите об этом, например, на стр. 288 работы: Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. В 3-х томах Том 1. — М.: Физматгиз, 1958. — 607 с.), но не разлагается по степеням х ни в какой окрестности нуля. Эта невозможность становится очевидной при переходе к комплексной переменной.

z = x + yi: у функции /(z) = exp (—у) точка z- 0 является существенно особой. Убедитесь в этом самостоятельно!

В заключение укажем еще одну связь комплексного анализа с действительным, связь между рядами Лорана и тригонометрическими рядами Фурье. Эта связь состоит в следующих утверждениях, выводы которых можно найти, например, в работе [16] на стр. 133−135.

Ряд Фурье интегрируемой функции (p (t), t е[0, 2/г], записанный в комплексной форме, является рядом Лорана функции f (z) = (/){(), где z = e", на единичной окружности | z= 1. И обратно, ряд Лорана функции f (z) на единичной окружности является рядом Фурье функции f{e^,') = (p{t) на отрезке [0,2*].

Пример 12.4. На отрезке [0,2*] разложить в ряд Фурье функцию.

Решение. Положив е" = z, привлекая равенства.

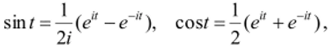
найдем соответствующую функцию.

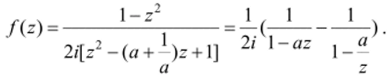
Она голоморфна в кольце {| а |<| z |< —}. Дважды используя геометрический.

N.

ряд, получим ее разложение в этом кольце.

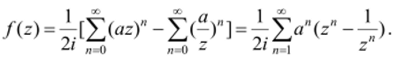
Заменяя здесь снова z — е", получим искомое разложение.

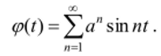
Задачи к главе 12.

12.1. Найти области сходимости рядов и их суммы:

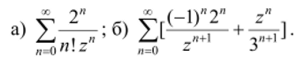
12.2. Найти правильную и главную части разложения функции в ряд Лорана по степеням z a) f (z) = ⁺ "; б) /(z) = sin- + cosz.

z — z Z

12.3. Требуется разложить данные функции в ряд Лорана в указанных кольцах:

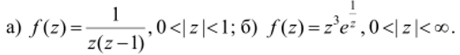
12.4. Найти изолированные особые точки функции и определить их тип:

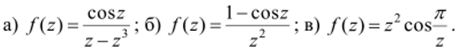
12.5. Пикар доказал следующую теорему, которая представляет собой далеко идущее обобщение основного свойства многочленов.

Любая функция, голоморфная в С, принимает вес значения в С, за исключением, быть может одного.

Проверьте этот факт для е^:.

• [1] 11. Лоран (1813−1854) французский математик, по профессии военный инженер.
• [2] Ш. Пикар (1856−1941) — французский математик. Основные труды в области дифференциальных уравнений.