Язык исчисления предикатов первого порядка

Основным инструментом представления знаний, рассматриваемым в этой главе, являются формулы прикладного исчисления предикатов первого порядка. Еще Д. Гильберт указал, что «исчисления предикатов первого порядка достаточно во всех разумных случаях». Мы рассматриваем здесь исчисление предикатов как язык, как систему обозначений для записи логических утверждений. Более того, мы считаем, что этот язык знаком читателю на уровне таких понятий, как логические связки («И», «ИЛИ», «ЕСЛИ … ТО») и кванторы («для всякого», «существует»)¹.

Мы рассматриваем язык, в котором участвуют логические связки, кванторы и атомарные формулы, построенные над множеством функциональных символов, предметных переменных и констант. Ниже приведена формальная грамматика (см. отступление в и. 2.3.3) языка исчисления предикатов первого порядка. При этом считаются заданными следующие множества отличимых друг от друга символов: множество символов констант (обозначение Конст), множество символов переменных (обозначение Перем), множество символов функций (обозначение Функ) и множество символов предикатов (обозначение Предикат).

Терм:

Список термов: Атом:

Литерал: Формула:

Связка: Квантор:

Конст | Перем | Функ (Список термов) Терм | Терм, Список термов Предикат | Предикат (Список термов) Атом | -л Атом Атом | —1 (Формула) |.

Формула Связка Формула) |.

Квантор Перем (Формула).

& | v | —>

V | 3.

Понятие литерала (атом или отрицание атома), вообще говоря, грамматически излишне. Мы ввели его, чтобы иметь под рукой этот термин. Предикат без аргументов также излишен. Мы ввели его для того, чтобы исчисление высказываний синтаксически было частным случаем исчисления предикатов.

Необходимо сделать несколько замечаний, касающихся грамматики этого языка:^[1][2]

• 1) в этом языке мы считаем, что наши функциональные и предикатные символы имеют фиксированные имена и фиксированное число аргументов, как в обычных системах программирования. Это довольно сильное допущение, и можно, в принципе, гак не считать. Однако при этом нам пришлось бы иметь дело с^{-выражениями} и смешанными вычислениями, что выходит за рамки данного курса;
• 2) язык, который мы используем, в логической иерархии классифицируется, как язык первого порядка. Другими словами, это означает, что под кванторами могут стоять только предметные переменные, т. е. не функциональные символы и не предикаты. В противном случае, т. е. если допускается, что квантор может связывать не только предметные переменные, то это будет уже исчисление не первого порядка. В реальных современных системах ИИ используются именно такие исчисления. Например, модное направление Model Checking основано на темпоральных логиках, которые выглядят как логики первого порядка, а на самом деле сводятся к стандартным логикам не первого порядка. Эти тонкости мы оставляем в качестве предмета для дополнений и не рассматриваем в основном русле примеров;
• 3) приведенная грамматика языка исчисления предикатов предполагает формальную запись утверждений в определенном синтаксисе, со всеми необходимыми скобками и т. д. В нашем рассмотрении примеров мы, естественно, сильно упростим формальный синтаксис и будем записывать формулы как удобнее, однако так, чтобы всегда можно было догадаться, какие синтаксические упрощения используются в том или ином случае. В частности, используется обычный приоритет связок и кванторов, лишние скобки систематически опускаются;
• 4) известно, что чистое исчисление предикатов первого порядка имеет ограниченную выразительную силу. Другими словами, многие содержательные теории невыразимы или трудно выразимы в чистом исчислении первого порядка, необходимы внелогические допущения. Естественно, что мы допускаем константы, функциональные символы и предикаты, которые нужны для описания предметной области. Но помимо этого, считается, что натуральные числа и другие общеизвестные понятия можно использовать в любых формулах, не пытаясь аксиоматически описать, что на самом деле это такое;
• 5) замкнутых формул вполне достаточно, и можно не рассматривать незамкнутые формулы, потому что если есть незамкнутая формула, то она будет выполнима тогда и только тогда, когда выполнимо соответствующее замыкание. Поэтому часто формулы записываются в открытой форме, при этом считается, что все свободные переменные замыкаются квантором всеобщности.

Что выразимо и что невыразимо в языке первого порядка В этом отступлении на примере некоторых понятий теории (абелевых) групп неформально устанавливаются границы применимости исчисления предикатов первого порядка.

Напомним, что теория групп может быть задана как прикладное исчисление предикатов с равенством, в котором имеются следующие собственные символы и аксиомы.

Предметная константа 0.

Двуместный функциональный символ +.

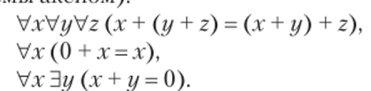
Собственные аксиомы (схемы яктмпмУ G1:

G2:

G3:

Заметим, что уже выражение «исчисление предикатов с равенством» означает, что подразумевается наличие двуместного предиката «равно», обозначенного знаком =, а также аксиом равенства и всех их следствий. Мы видим, что в общепринятую аксиоматику теории групп включены не все реально используемые собственные предикаты и аксиомы. Можно согласиться, однако, с тем, что такое использование предиката равенства не выводит за пределы языка исчисления предикатов первого порядка, а является просто принятым в математике синтаксическим сокращением. Продолжим рассмотрение примера.

Группа называется абелевой, если имеет место собственная аксиома G4: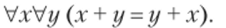

Говорят, что в абелевой группе все элементы имеют конечный порядок, ограниченный числом п, если выполнена собственная аксиома G5: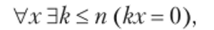

здесь kx — это сокращение для х + х + … + х, где .г повторяется k раз.

Эта формула не является формулой теории групп, поскольку содержит «посторонние» предметные предикаты (предикат <) и переменные (к и п). Однако для любого конкретного конечного п собственная аксиома может быть записана в виде допустимой формулы теории групп:

G5':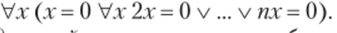

Абелева группа называется делимой, если выполнена соОствениая аксиома G6: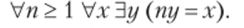

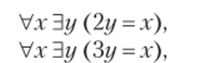
Эта формула не является формулой теории, поскольку содержит «посторонние» предметные константы (константа 1), предикаты (>) и переменные. Однако собственная аксиома может быть записана в виде бесконечного множества допустимых формул теории групп:

G6'.

Можно, однако, показать, что любое конечное множество формул, истинное во всех делимых абелевых группах, истинно и в некоторой неделимой абелевой группе, т. е. теория делимых абелевых групп не является конечно аксиоматизируемой. Абелева группа называется периодической, если выполнена собственная аксиома G7: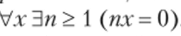

Эта формула также не является формулой теории групп, поскольку содержит «посторонние» предметные константы и переменные. Если попытаться преобразовать формулу G7 по образцу формулы G5, то получится бесконечная «формула» G7':

которая не является допустимой формулой исчисления предикатов и тем более теории групп. Таким образом, теория периодических абелевых групп не является аксиоматизируемой, если не включать в теорию групп и всю формальную арифметику. Но включение в аксиоматику формальной арифметики влечет более серьезные последствия, по сравнению с включением теории равенства. Это устанавливается знаменитыми теоремами Геделя о неполноте.

Давно известны некоторые важные свойства формальных теорий, в частности, прикладных исчислений предикатов первого порядка, которые существенным образом влияют на практическую применимость формальных теорий (аксиоматического метода). Полное доказательство этих фактов выходит далеко за рамки данного учебника. Однако понимание границ применимости формальных методов является, но нашему мнению, необходимым для использования таких методов.

Поэтому ниже приводятся (без доказательства и в упрощенной формулировке) два важнейших факта, известные как теоремы Геделя о неполноте.

Аксиоматический метод обладает множеством достоинств и с успехом применяется на практике для формализации самых разнообразных предметных областей в математике, физике и других науках. Однако этому методу присуще следующее принципиальное ограничение.

Теорема 4.1 (первая теорема Геделя о неполноте). Во всякой достаточно богатой теории первого порядка (в частности, во всякой теории, включающей формальную арифметику) существует такая истинная формула F, что ни F, ниiFne являются выводимыми в этой теории.

Утверждения о теории первого порядка также могут быть сформулированы в виде формул теории первого порядка. В частности, утверждения о свойствах формальной арифметики (например, утверждение о непротиворечивости формальной арифметики) могут быть сформулированы как арифметические утверждения.

Теорема 4.2 (вторая теорема Геделя о неполноте). Во всякой достаточно богатой теории первого порядка (в частности, во всякой теории, включающей формальную арифметику) формула F, утверждающая непротиворечивость этой теории, не является выводимой в ней.

Вторая теорема Геделя нс утверждает, что арифметика противоречива^[3]. Эта теорема утверждает, что непротиворечивость достаточно богатой формальной теории не может быть установлена средствами самой этой теории. При этом вполне может статься, что непротиворечивость одной конкретной теории может быть установлена средствами другой, более мощной формальной теории. Но тогда возникает вопрос о непротиворечивости этой второй теории и т. д.

Наличие неаксиоматизируемых и конечно неаксиоматизируемых формальных теорий не означает практической неприменимости аксиоматического метода на основе использования языка исчисления предикатов первого порядка. Это означает, что аксиоматический метод не применим «в чистом виде». На практике формальные теории, описывающие содержательные объекты, задаются с помощью собственных аксиом, которые наряду с собственными предикатами и функциональными символами содержат «внелогические» предикаты и функциональные символы, свойства которых аксиомами не описываются, а считаются известными (в данной теории). В рассмотренных примерах внелогическими являются натуральные числа и операции над ними. Аналогичное обстоятельство имеет место и в системах логического программирования типа Пролог, и в прикладных системах ИИ. Реализация такой системы всегда снабжается обширной библиотекой внелогических (или встроенных) конструкций, которые и обеспечивают практическую применимость систем логического программирования и представления знаний формулами исчисления предикатов в ИИ.

Курт Фридрих Гедель (нем. Kurt Friedrich Godcl), 1906 1978 — австрийский логик, математик и философ науки. Наиболее известное достижение Геделя — это сформулированные и доказанные им теоремы о неполноте, опубликованные в 1931 г.

«Время — это отнюдь не специфическая характеристика бытия. Я не верю в объективность времени. Время — субъективно».

• [1] 1 Ранее мы уже использовали некоторые обозначения исчисления предикатов (кванторы
• [2] 3 и связку —?) без определений, именно в расчете на то, что читатель их знает.
• [3] Формальная арифметика как раз непротиворечива!