Агрегатные состояния и фазовые переходы.
Изотермы Ван-дер-Ваальса
В промежуточной области сводящееся к кубическому относительно объема уравнение (14.4) может иметь два экстремума или не иметь их. Анализ показывает, что два экстремума имеют место при невысокой температуре. При этом на изотермах есть участок, где давление растет с увеличением объема, что не имеет физического смысла. При повышении температуры этот участок уменьшается и превращается в точку. Эта… Читать ещё >
Агрегатные состояния и фазовые переходы. Изотермы Ван-дер-Ваальса (реферат, курсовая, диплом, контрольная)
Агрегатное состояние — состояние вещества, характеризующееся способностью сохранять объем и форму, характером дальнего и ближнего порядка взаимодействия молекул и т. д. Выделяют следующие агрегатные состояния: твердое, жидкое, газообразное, плазму и др. Фазовые переходы это термодинамические процессы, приводящие к изменению агрегатного состояния вещества. Изменение агрегатного состояния обычно сопровождается скачкообразным изменением энтропии, плотности и других основных физических свойств вещества.
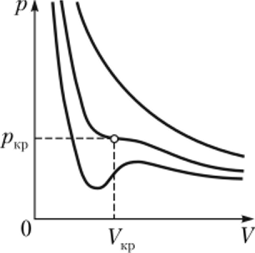
Рис. 14.2.
Уравнение Ван-дер-Ваальса может быть использовано для количественных расчетов, пока добавленные члены являются поправками. Однако его можно применять и для качественных оценок изменений агрегатного состояния вещества, в частности перехода вещества из газообразного состояния в жидкое. Рассмотрим поведение изотерм Ван-дер-Ваальса — зависимости давления от объема при постоянной температуре, определяемой уравнением Ван-дер-Ваальса для различных температур (рис. 14.2). Уравнение реального газа (14.4) можно представить в виде, удобном для анализа:

Из этого уравнения видно, что при V —> оо доминирует левый член зависимости и давление, как и для идеального газа, убывает по гиперболическому закону:

В промежуточной области сводящееся к кубическому относительно объема уравнение (14.4) может иметь два экстремума или не иметь их. Анализ показывает, что два экстремума имеют место при невысокой температуре. При этом на изотермах есть участок, где давление растет с увеличением объема, что не имеет физического смысла. При повышении температуры этот участок уменьшается и превращается в точку. Эта точка называется критической. Значения давления, объема и температуры в этой точке называют критическими параметрами. В критической точке кривая имеет точку перегиба, так что обращаются в нуль как первая, так и вторая производные. Из этого условия несложно найти критические параметры:
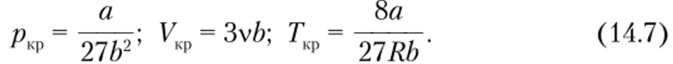
Экспериментальные состояния газа (рис. 14.3) отличаются тем, что нефизичный и противоречащий здравому смыслу участок, где давление растет с увеличением объема, заменяется на горизонтальный участок, соответствующий сжижению газа, которое при заданной температуре происходит при постоянном давлении. Слева от горизонтального участка весь газ превращается в жидкость. При этом давление на эксперименте растет с уменьшением объема более резко, чем в теории.
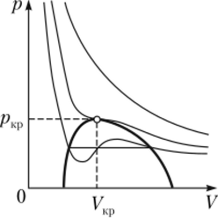
Набор отрезков зависимости давления от объема реального газа, соответствующих двухфазным системам жидкость — газ, образуют колоколообразную фигуру (на рис. 14.3 ограничена сверху жирной линией). Вершиной этой фигуры является критическая Рис. 143 точка. При температуре выше критической вещество может существовать только в газообразном состоянии. При температуре ниже критической вещество может быть превращено в жидкость. У гелия, водорода, кислорода и азота критические температуры низкие, и при нормальных условиях они являются газами. У воды и ртути критические температуры высокие, и при нормальных условиях они существуют как в жидком, так и в газообразном состоянии.