Обобщенная процедура оценки остаточного риска методами теории подобия

После уяснения сущности соответствующего подхода логично изложить рекомендации по подбору аналогов конкретного элемента ОТУ с целью объединения сведений, полученных при их эксплуатации, с данными о результатах последнего диагностирования его технического состояния. Ведь совместное использование подобной (априорной и только что полученной) информации повысит достоверность оценивания числовых характеристик m_t, m_v, а² и а², а значит, и зависимостей V (t), L (t| V) и ДО, используемых для прогноза остаточного ресурса. Сделать это необходимо еще и потому, что сходные с m_t и а² параметры, входящие в условные производящие функции Af (S) моментов времени, потребуются также для оценки остаточного ресурса с помощью GERT-модели.

Предлагаемая процедура состоит из следующих основных этапов и действий.

Этап I. Выбор и обоснование объектов-аналогов, наиболее подходящих для прогноза ресурса безопасной эксплуатации критически значимых механических элементов данного ОТУ.

• 1. Главное внимание при подборе подобных аналогов следует уделять идентичности целевого предназначения и однотипности протекающих физических процессов. В частности, аналогами механического оборудования паровых турбин теплоэлектростанций могут быть те газовые турбины, реакторы и центрифуги химической и атомной промышленности, которые длительно работают под воздействием высокого внутреннего давления и повышенных рабочих температур.
• 2. Первоочередному рассмотрению подлежат физические процессы и параметры, больше других влияющие на достижение выбранным конструктивным элементом наиболее вероятных предельных состояний. При составлении их перечня целесообразно руководствоваться наработками вероятностной механики разрушений и приведенной выше (см. параграф 7.1) классификацией, а также достоверными статистическими данными по однотипному оборудованию.
• 3. При сборе и обработке эмпирических и диагностических данных по исследуемым элементам следует исходить из возможности их последующего использования для определения критериев (констант или инвариантов) подобия, характеризующих протекание доминирующих физических процессов и наступление возможных предельных состояний.

Этап II. Составление зависимостей между выбранным определяющим параметром повреждаемости конструкционного материала механического элемента и учитывающими ее показателями остаточного ресурса, что необходимо для определения начальной длины 1₀ трещин и средней скорости V их развития. С учетом выбранного выше механизма постепенной утраты сплошности 'Р рекомендуется следующий порядок решения этой задачи [33, 35].

1. В общем случае скорость dV/dx утраты сплошности (накопления повреждаемости) любого материала под воздействием внешних нагрузок F и время x_d его перехода в соответствующее предельное состояние могут быть представлены следующими векторными выражениями:

где В > 0, т > О — константы эволюционной утраты сплошности конструкционным материалом; т* < x_d и F_d — время нагружения и критическая для него нагрузка.

2. При наличии в механическом элементе галтелей, отверстий, сварных швов и других конструктивных концентраторов напряжения, формирующих зону потенциального разрушения, определяющим (для страгивания и распространения трещины) параметром целесообразно считать максимальное значение коэффициента К интенсивности напряжений или размах АК его номинальной величины. Их величины могут быть рассчитаны по следующим формулам:

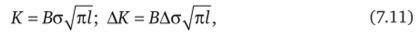
где В — коэффициент, зависящий от геометрии трещины на поверхности этого элемента, направления доминирующей для него нагрузки и типа конструктивного концентратора напряжения; ст, До — амплитуда и размах напряжения, возникающего в соответствующей потенциальной зоне разрушения материала; I — длина имеющейся трещины.

3. Долговечность механического элемента, подвергнутого одновременному воздействию высоких температур и циклических нагрузок, также может быть оценена по правой формуле (7.10), но при условии замены F на К_с, а времени x_d на число N_d циклов нагружения, способных привести к появлению или страгиванию усталостных трещин:

где ЛГ — число циклов нагружения механического элемента; К_с, К_тах — коэффициенты интенсивности напряжений: приводящий к утрате конструкционным материалом статической вязкости и максимально действующий в нем.

4. Выражение для скорости V развития трещины в элементе определяется путем перехода от х к ЛГ, замены в формулах (7.10) параметра F_d на К_тах, а производной d’F/dx — на (.d'V/dl) (dl/dN) и интегрирования полученного выражения после разделения его переменных и с учетом левой части (7.11). В результате получаем.

где У" — параметр, характеризующий величину прироста (скачок) трещины (см/цикл).

Так как система (7.13), правая половина которой представляет уравнение Пэриса, содержит параметры, в общем случае не поддающиеся определению, несмотря на однозначную взаимозависимость и V, для оценки скорости V развития трещины обычно рекомендуется привлекать дополнительную (полуэмпирическую) информацию.

В частности, для наружной части диска паровых турбин эта скорость чаще всего равна.

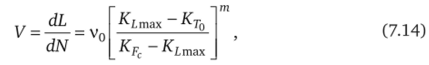
где K_Lmax, K_F = 2,13 — максимально возможный и критический коэффициенты интенсивности напряжений, действующих в зоне потенциального разрушения металла диска; К_То — минимально-пороговая величина коэффициента интенсивности напряжений, приводящих к страгиванию трещины; v₀, ш — константы, характеризующие особенности циклического нагружения диска и его конструкционного материала. Значения трех последних величин рекомендуется рассчитывать с учетом коэффициента A = K_min/K_max асимметрии цикла нагрузки по следующим эмпирическим формулам [35]:

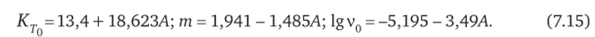
Для приближенной оценки скорости развития трещин в элементах остального тепломеханического оборудования паровой турбины может быть использовано следующее эмпирическое выражение, полученное на основе анализа многочисленных экспериментальных данных:

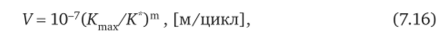
где 10^-7 — скачок прироста V" трещины (см. первую из формул (7.13)) на величину размера среднего зерна субструктуры металла в зоне его разрушения.

Этап III. Принятие решения о возможности объединения результатов диагностики технического состояния рассматриваемого элемента с соответствующими данными его аналогов. При реализации этого этапа следует руководствоваться основными принципами выявления стохастического подобия и использовать модели переноса необходимой информации.

1. Определение по выборочной совокупности (t_p t₂, …, t_n) числовых характеристик m₍, ст₍ нормально распределенного времени наступления предельного состояния. Данную задачу параметрического оценивания следует решать методом максимального правдоподобия (см. параграф 2.5), т. е. подбором таких оценок m = 0_x(f) и о₍= 0_х(г) параметров соответствующей плотности/(t, 0), которые максимизируют величину следующей функции:

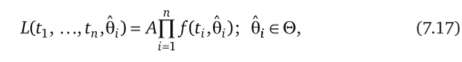
где Л — векторная величина, не зависящая от оценок 0 и их плотности /(Г, 9,); L (t_v …, t_n,0^ — функция правдоподобия имеющихся эмпирических данных.

2. Подтверждение однородности объединяемой информации о времени достижения элементом предельного состояния осуществляется путем проверки двух статистических гипотез (см. параграф 2.6):

a)/(t) — о принадлежности эмпирически найденного распределения Н₀⁽²⁾ этого времени нормальному закону; б) Н₀⁽²⁾ —о равенстве числовых характеристик т₍ и о₍ соответствующего времени для выбранных ранее аналогов конкретного механического элемента. Эту задачу следует решать с помощью плотностей/(t, 0) и fit, 0), которые станут аргументами функции ф (П (f (t, 0);/(t_p…, t_n, 0₍))) распределения критериев П (0 стохастического подобия и критическое значение которых затем используется при принятии решения о справедливости выдвинутых статистических гипотез или их отклонения в пользу альтернативных — Н^ Н®

Если конкретнее, то порядок проверки этих статистических гипотез включает следующие основные этапы:

• а) сбор информации о повреждаемости П аналогов и ее обработка с целью построения эмпирического распределения /(t) и точечного оценивания его параметров m_t, а_г Осуществляется в соответствии с изложенными выше принципами математической статистики, касающимися формирования выборки, группировки данных по интервалам и их представления в форме гистограмм, нахождения выборочного среднего и его дисперсии;
• б) выдвижение статистических гипотез H_Q⁽¹⁾, Н® и выбор критерия П^(,)(/) их проверки. При известном виде плотности ср (П (/Д, 0), f (t_v t₂, t_n, 0_t))) вероятности распределения его значений (Гаусса,

Стьюдента, Фишера, хи-квадрат) для проверки этих гипотез привлекаются следующие критерии: 1) Колмогорова — для распределения /(t_p t₂, t_n, 0), сильно отличающегося от теоретического на небольшом интервале времени (t₂— t_x); 2) омега-квадрат — при малозаметном отличии результатов наблюдений на всем диапазоне (t_n— t_});

• 3) хи-квадрат — для больших выборок эмпирических данных, если произведение их числа на вероятность появления в каждом интервале укладывается в отрезок [0; 5];
• в) выбор доверительной вероятности у, определяющей уровень значимости (1 — у) нулевых гипотез Н^ Н^² расчет соответствующих ему значений критерия проверки П^^1](/) либо П?²⁾(/), определение по статистикам /(t, 0j), /(Г, 0₂) выборочных критериев П⁽ '⁾(/'(Г, 0),/(г_], t₂, t_n, 0₍)) и сравнение этих значений с целью принятия решения по следующему правилу:

где П^(|), П⁽²⁾ и П?'^)Н, П?*^)Е — критерии проверки, полученные расчетом по эмпирическим данным аналогов, и их критические (нижнее и верхнее предельно допустимые) значения. Если соблюдено условие (7.18), то объединение данных о параметрах повреждаемости аналогов и исследуемого элемента возможно, а если имеем условие (7.19), то подобное решение следует отложить.

3. Объединение данных по аналогам и диагностике технического состояния исследуемого конструктивного элемента. Идея решения данной задачи для сужения доверительных границ оценки гамма-процентного ресурса Г байесовским методом была продемонстрирована выше (см. рис. 7.1). Поэтому при найденной этим способом апостериорной плотности <�р (Г_у | ?, со, щ) вероятности предельного состояния конструктивного элемента значение нижней доверительной оценки его остаточного ресурса можно найти с помощью уравнения.

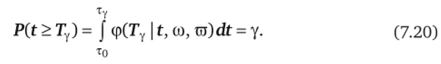
Таким образом, рассмотренная здесь методика априорной количественной оценки остаточного ресурса критически значимых механических элементов ОТУ является довольно совершенной, так как включает в себя ретроспектирование, т. е. анализ прошлого, диагностирование — определение настоящего и прогнозирование как оценку будущего. Именно поэтому она и рекомендуется для повышения обоснованности соответствующих решений риск-менеджмента за счет снижения возможных ошибок первого и второго рода.