Особенности описания биохимических процессов

Биохимические процессы осуществляют превращение одной субстанции в другую с помощью живых клеток, однако более рационально и экономично, чем химическое превращение. И для них широко используется математический аппарат описания многофазных химических реакторов. Ферментационная среда представляет собой многофазную систему, содержащую пузырьки газа (аэрирующий газ — источник кислорода), питательную жидкость и квазитвердую фазу (клетки — продуценты биомассы). Гидродинамика такой системы чрезвычайно сложна, поэтому чаще всего анализ структуры потоков сводится к псевдогомогенной системе (водная фаза — клетки). Но даже и в общем случае модели структуры потоков и массопереноса, полученные для процессов химического превращения, с учетом характерных особенностей могут быть использованы при исследовании биохимических реакторов. Одним из важных этапов разработки математической модели биохимического реактора является этап формирования кинетической модели.

Таблица 2.4. Математические описания каталитических гомогенных н гетерогенных реакторов

Примечание, v — линейная скорость подвижной фазы; а — коэффициент теплоотдачи; Т" — температура стенки реактора; d — диаметр реактора; а — поверхность раздела фаз; Т*.

с* - температура и концентрация компонента на поверхности раздела фаз соответственно; Kg — коэффициент массоотдачи; с — порозностъ слоя^/дф и Дэф — эффективный коэффициент продольной и поперечной диффузии соответственно; Х/^ф и Х^ф — эффективный коэффициент продольной и поперечной теплопроводности соответственно; D^ф — эффективный коэффициент в грануле катализатора; и X*j> - теплопроводности, соответствующие Di и 0‘_уф; R ;

радиус гранулы; а' - коэффициент теплоотдачи потока в грануле катализатора; V_bx, g — прямой и обратный потоки соответственно; индексы m и т относятся к веществу и теплу соответственно; / - число компонентов; к — число ячеек.

Кинетическая модель представляет собой скорость развития общей численности популяции и отражает влияние на нее комплекса факторов окружающей среды, в которой популяция развивается. При этом в процессе роста может изменяться и качественный состав популяции, что в свою очередь оказывает влияние на скорость накопления биомассы и продуктов метаболизма.

Если представить, что биомасса по составу является неоднородной и обозначить через х, (/ = 1, 2, …, п) общее количество |-го компонента в единице объема, то состояние популяции в момент времени t будет характеризоваться набором x,{t).

Примем, что состояние популяции меняется в некоторой среде под действием внешних факторов ^{/) (J = 1,2, …, /, где / - число внешних факторов, характеризующих состояние среды).

К внешним воздействиям (факторам) относятся концентрации субстрата, продуктов метаболизмов, элементов минерального питания, температура, pH среды и др.

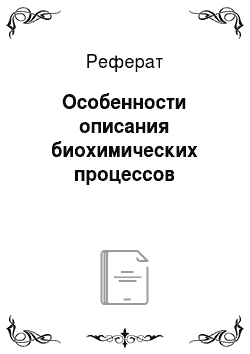
Полагая, что состояние популяции в момент времени t + At зависит только от состояния в момент времени t и внешних воздействий Z (/), и введя в рассмотрение скорость увеличения численности /-го состава /?,(х, ?, 0), получим изменение полной концентрации биомассы:

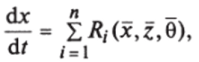
где 0 — вектор параметров модели; х — концентрация биомассы.

Так, например, скорость роста утилизации субстрата для модели Моно можно выразить через коэффициент использования субстрата (ср) и экономический коэффициент а^х следующим образом: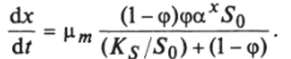

Скорость роста клеток микроорганизма имеет вид:

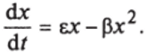
Решение этого уравнения представлено ниже:

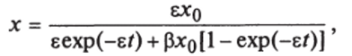
где ф = (5q — S)/5b; а* = /a^s a^s — расходные коэффициенты субстрата биомассы; Ks ~ концентрация субстрата при скорости роста ц = i, J2; So, S — начальная и текущая концентрации субстрата; ц_т — максимальная удельная скорость роста микроорганизмов; х = хо при г = 0 (концентрация исходной или засевной биомассы).

Скорость роста клеток в зависимости от концентрации субстрата и продуктов метаболизма может быть представлена в виде модели Моно — Иерусалимского:

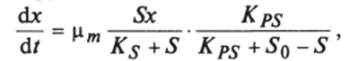
где Kps = KfiSo — 5)/Л Р — концентрация продукта метаболизма.

Наиболее полное представление о динамике роста клеточной популяции дают кинетические модели, учитывающие возрастную или физико-биохимическую неоднородность клеток.

Обобщением структурных моделей, учитывающих возрастную и физиологическую неоднородности, служит модель статики и динамики клеточной популяции.

Итак, технологический расчет аппарата заключается в разработке соответствующего математического описания, выборе метода решения системы уравнений этого описания, определении необходимых параметров, установлении адекватности модели реальному объекту, т. е. в разработке математической модели объекта. Независимо от функционального назначения элемента схемы математическая модель должна строиться по модульному принципу, причем таким образом, чтобы можно было иметь возможность при необходимости достаточно легко внести нужные изменения (дополнения или расширения функций) в модель без ее значительной переработки. Основная функция модели состоит в сведении материального и теплового балансов — получении выходных данных потока по входным данным. В зависимости от назначения математического описания отдельных явлений процесса (фазовое и химическое равновесие, кинетика массопередачи, гидродинамика потоков и т. д.) общее математическое описание может существенно различаться. Важно при создании модели не нарушать общей ее структуры, т. е. иметь возможность использования единых алгоритмов решения.