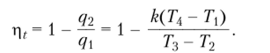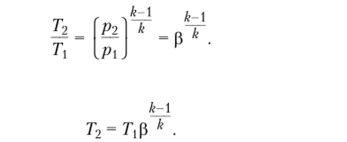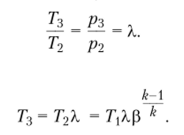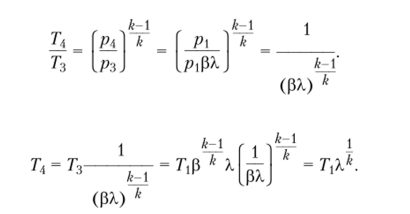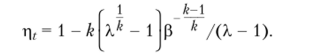Циклы ГТУ с подводом теплоты при постоянном объеме

В отличие от ГТУ со сгоранием топлива при постоянном давлении, где процесс горения осуществляется непрерывно, в ГТУ со сгоранием топлива при постоянном объеме процесс горения является периодическим (пульсирующим). Через воздушный клапан 7 в камеру сгорания 1 поступает воздух, сжатый в компрессоре 6 (рис. 8.5).

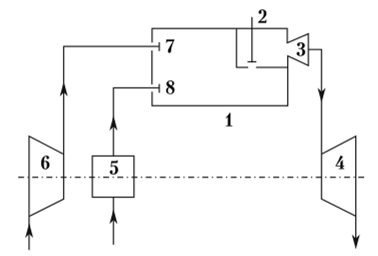
Рис. 8.5. Принципиальная схема ГТУ со сгоранием топлива при постоянном объеме.

Сюда же топливным насосом 5 через топливный клапан 8 подается жидкое топливо. Процесс горения производится при закрытом воздушном клапане 7 и закрытом сопловом клапане 2. Воспламенение происходит от электрической искры. После сгорания топлива в результате повышения давления в камере 1 открывается сопловой клапан 2. Продукты сгорания, проходя через сопловые аппараты 3, поступают на лопатки газовой турбины 4.

Идеальный цикл газотурбинной установки с подводом теплоты при постоянном объеме в pv- и 7л-диаграммах представлен па рис. 8.6.

В адиабатном процессе (линия 1—2) рабочее тело с параметрами р_х, V, Т в точке 1 сжимается до параметров р>, v₂, Т₂ в точке 2.

В изохориом процессе (линия 2—3) к рабочему телу подводится некоторое количество теплоты q. Затем рабочее тело расширяется в адиабатном процессе (линия 3—4) до начального давления = р и по изобаре (линия 4—1) возвращается в первоначальное состояние, характеризуемое параметрами точки 1. Характеристики цикла: (3 = р₂/р — степень повышения давления в компрессоре; X = р₂/р₂ — степень добавочного повышения давления.

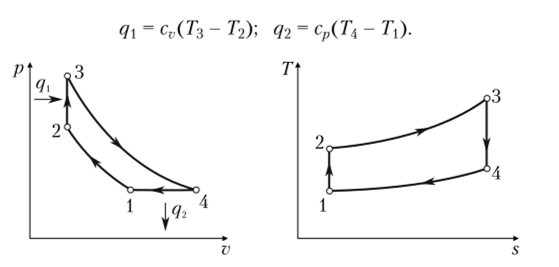
Рис. 8.6. Идеальный цикл ГТУ с подводом теплоты при постоянном объеме в pv- и 7х-диаграммах Удельные количества подводимой и отводимой теплот определяются по формулам Подставляя эти величины в соотношение для термического КПД, получаем формулу.

Найдем выражения для температур Т₂, Т₂, через начальную температуру Т. В адиабатном процессе (линия 1—2) имеем формулу Отсюда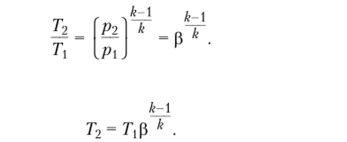

В изохорном процессе (линия 2—3).

Отсюда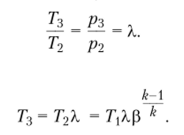

В адиабатном процессе (линия 3—4).

Отсюда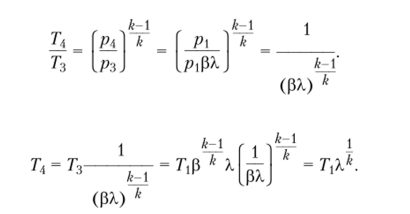

Подставляя найденные значения температур в выражение для термического КПД, получаем формулу.

Из данной формулы видно, что термический КПД возрастает с возрастанием величин X, р, к.