Основные положения метода (алгебраические координатные функции)

Рассмотрим методику определения собственных чисел, основанную на совместном использовании метода Фурье и методов взвешенных невязок. При таком подходе на первоначально принимаемое решение в виде простого алгебраического или тригонометрического полинома не накладывается никаких предварительных условий. Неизвестные коэффициенты решения определяются из выполнения основных и дополнительных граничных условий. Собственные числа находятся путем интегрирования невязки дифференциального уравнения Штурма —Лиувилля либо из условия ортогональности невязки к собственной функции.

В качестве конкретного примера рассмотрим задачу теплопроводности для бесконечно протяженной пластины при граничных условиях первого рода: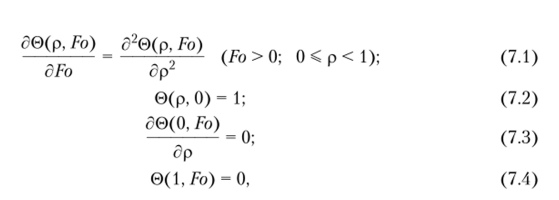

где 0(р, Fo) = (Т- 7'_ст)/(7'о — Т_ст) — относительная избыточная температура; Т_ст — температура пластины при р = 1; р = х/8 — безразмерная координата; 8 — половина толщины пластины; Т₀ — начальная температура; Fo = ах/8² — число Фурье; а — коэффициент температуропроводности; т — время. Следуя методу Фурье, решение задачи (7.1)—(7.4) принимается в виде.

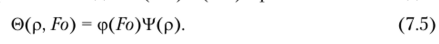
Подставляя (7.5) в (7.1), находим соотношение.

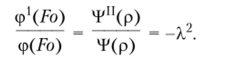
Отсюда получаем два обыкновенных дифференциальных уравнения.

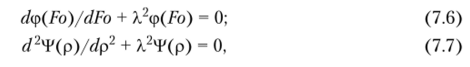
где X² — некоторая постоянная.

Решение уравнения (7.6) имеет вид.

где А — неизвестный коэффициент.

Уравнение Штурма — Лиувилля (7.7) представим следующим образом:

где р = Я².

Граничные условия для уравнения (7.9) согласно (7.3), (7.4) будут иметь вид

Решение задачи (7.9)—(7.11) разыскивается в виде ряда.

где Cj (i = 0, п) — неизвестные постоянные, определяемые из граничных условий задачи; Л^г,(р) = р' — координатные функции (алгебраический или тригонометрический полином).

Если ограничиться, например, пятью членами ряда (7.12) (п = 4), то будем иметь пять неизвестных коэффициентов С, (г = 0,4), а граничных условий только два (7.10), (7.11). Поэтому необходимо добавить еще три дополнительных граничных условия, которые находятся из условия (7.10) и из уравнения (7.9) путем выполнения этого уравнения, а также соотношений, полученных после взятия производных от него различного порядка в граничных точках р = 0 и р = 1. Такие дополнительные граничные условия будут иметь вид.

Необходимость введения дополнительных граничных условий объясняется тем, что в уравнениях (7.6), (7.7) появляется новый неизвестный параметр р, который находится из характеристического уравнения, получаемого в результате подстановки (7.12) в дифференциальное уравнение (7.9). В зависимости от числа членов ряда (7.12) вводится соответствующее число дополнительных граничных условий и в итоге получается соответствующее количество собственных чисел.

Подставляя (7.12) в (7.10), (7.11), (7.13)—(7.15), получим пять алгебраических линейных уравнений относительно пяти неизвестных C_v При этом каждое из неизвестных С₀, C_lt С₂ входит лишь в одно уравнение, из которого оно легко определяется. Все эти уравнения получаются из граничных условий при р = 0 (условия (7.10), (7.13), (7.15)). Относительно неизвестных С₃, С₄ необходимо решить два взаимосвязанных алгебраических линейных уравнения. В итоге для всех искомых неизвестных постоянных будем иметь значения.

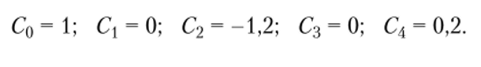
Подставляя найденные значения С в (7.12), получаем соотношение.

Для определения первого собственного числа найдем интеграл взвешенной невязки уравнения (7.9), т. е.

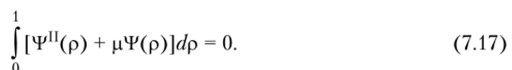
Подставляя (7.16) в (7.17), относительно р получаем характеристическое уравнение, из которого находим pj = 2,5. Точное значение первого собственного числа pi = 2,46 740 110 027 [49].

Для уточнения первого собственного числа составим невязку уравнения (7.9) и потребуем ортогональность невязки к собственной функции (7.16):

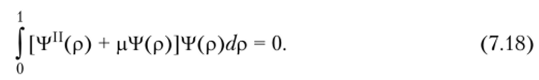
Подставляя (7.16) в (7.18), относительно р получаем характеристическое уравнение.

0,5 038 730 158 730 159р — 1,243 428 571 429 = 0.

Его решение p_t = 2,46 774 193.

Следовательно, выполнение требования ортогональности невязки уравнения (7.9) к собственной функции (7.16) приводит к существенному уточнению первого собственного числа.

Для получения первых двух собственных значений вводятся дополнительные граничные условия, получаемые из уравнения (7.9),.

В итоге получается всего семь граничных условий — два основных (7.10), (7.11) и пять дополнительных (7.13)—(7.15), (7.19), (7.20). Следовательно, для определения коэффициентов С, (г = 0, 6) следует использовать семь членов ряда (7.12).

Подставляя (7.12) при п = 6 во все граничные условия задачи, относительно Ci получим семь алгебраических уравнений. Пять из этих уравнений разделяются, т. е. в одно уравнение входит лишь одно неизвестное. Таким образом находятся значения неизвестных.

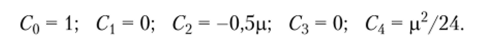
Значения неизвестных С5, Q находятся из системы двух алгебраических уравнений, составленных из граничных условий при р = 1, т. е. из граничных условий (7.11), (7.14). Из решения этой системы находим значения.

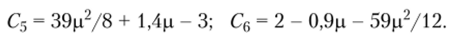
После подстановки коэффициентов С_х в (7.12) составляется интеграл взвешенной невязки уравнения (7.9). Отсюда для определения собственных чисел получается характеристическое уравнение Его решение р] = 2,4 669 819; р₂ ⁼ 21,794 472 203.

Для уточнения первых двух собственных чисел требуется ортогональность невязки уравнения (7.9) к собственной функции (7.12) при /7 = 6. Для определения собственных чисел получается характеристическое уравнение вида.

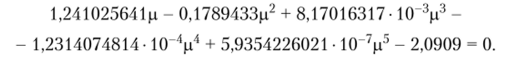
Его решение pi = 2,46 740 110; р₂ ⁼ 22,26 983.

Ввиду того что уравнение (7.9) удовлетворяется лишь при некоторых дискретных значениях р (собственных значениях, образующих спектр), остальные корни уравнения (три корня) следует отбросить как не удовлетворяющие этому уравнению (в чем можно убедиться непосредственной подстановкой).

Как видно, первое собственное число до девятого знака совпадает с точным его значением. Точное значение второго собственного числа 1491 р₂ = = 22,206 609 902.

Собственные функции находятся из (7.12).

Для получения трех собственных чисел ко всем имеющимся граничным условиям добавляются дополнительные граничные условия вида.

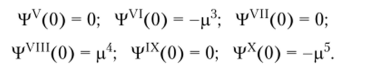
В данном случае для первых трех собственных чисел получаются следующие значения (найдены с учетом ортогональности невязки уравнения (7.9) к функции (7.12)): р, = = 2,4 674 011 001; р₂ = 22,2 066 135; р₃ = 62,55 342. Отметим, что точное значение третьего собственного числа составляет р₃ = = 61,68 502 750 [49].

Для получения пяти собственных чисел используются следующие дополнительные граничные условия:

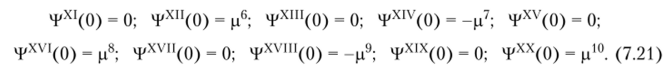
В этом случае имеем значения pj = 2,4 674 011 002; р₂ = 22,206 610; р₃ = = 61,6 850 235; р₄ = 120,90 249; ps = 201,0584. Точные значения четвертого и пятого собственных чисел р₄ = 120,90 265; р₅ = 199,8595.

Подставляя (7.8), (7.12) в (7.5), для каждого собственного числа будем иметь частные решения вида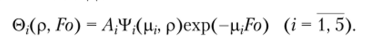

Каждое частное решение точно удовлетворяет граничным условиям (7.3), (7.4) и приближенно (в пятом приближении) удовлетворяет уравнению (7.1) на отрезке 0 < р < 1. Однако ни одно из этих частных решений, в том числе и их сумма.

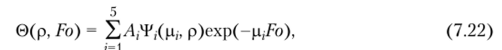
не удовлетворяют начальному условию (7.2).

Для выполнения начального условия составляется его невязка и требуется ортогональность невязки к каждой собственной функции, г. е.

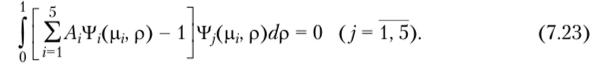
Определяя интегралы в (7.23), для нахождения коэффициентов Л, (/ = 1,5) получаем систему пяти алгебраических линейных уравнений. Ее решение имеет вид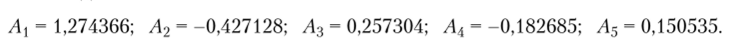

Приведенные здесь коэффициенты Л, найдены из уточненных значений собственных чисел (путем требования ортогональности невязки уравнения (7.9) к функции (7.12)).

Собственные числа для различных приближений в сравнении с точными их значениями приведены в табл. 7.1 (для каждого приближения верхняя строка — без ортогональности, нижняя — с ортогональностью невязки уравнения (7.9) к функции (7.12)).

Результаты расчетов безразмерных температур по формуле (7.22) в сравнении с точными их значениями [49] представлены на графиках рис. 7.1 и 7.2.

Анализ результатов расчетов позволяет заключить, что в пятом приближении температуры, полученные по формуле (7.22), в диапазоне чисел Фурье 0,008 < Fo < °° практически совпадают с их точными значениями.

Таким образом, в методе Бубнова—Галеркина требуется удовлетворить условиям ортогональности невязки первым п функциям некоторой полной в данной области системы линейно-независимых функций. Из теории рядов Фурье [ 281 следует, что равенство невязки нулю (а это имеет место при точном решении уравнения (7.9)) равносильно требованию ортогональности ее ко всем функциям У, системы. Имея, однако, в своем распоряжении лишь п членов полинома (7.12) (или п постоянных С,), мы можем удовлетворить только п условиям ортогональности, что и приводит лишь к приближенному решению.

Таблица 7.1

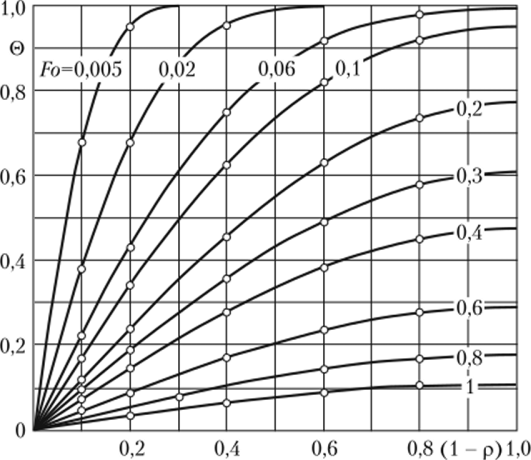
Рис. 7.1. Изменение относительной избыточной температуры в пластине:

— точное решение [49]; о — по формуле (7.22).

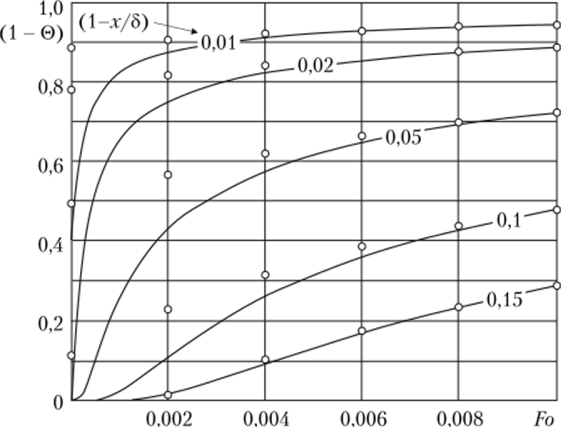
Рис. 7.2. Изменение температуры в пластине:

—точное решение [49]; о — по формуле (7.22).

Следует отметить высокую точность определения собственных чисел по сравнению с другими методами совместного использования точных и приближенных методов. К числу таких методов относятся: совместное использование интегральных преобразований Лапласа и метода Бубнова —Галеркина [83], методов Фурье и Канторовича [27, 28, 46], методов Фурье и Бубнова — Галеркина (без использования дополнительных граничных условий). Все эти методы для одних и тех же задач приводят к мало отличающимся результатам. В качестве конкретного примера в табл. 7.2 приведены собственные числа для четвертого и пятого приближений, полученные при решении задачи (7.1)—(7.4) путем совместного использования интегральных преобразований Лапласа и метода Бубнова —Галеркина.

Отметим, что последние собственные числа как в четвертом, так и в пятом приближениях почти в два раза отличаются от их точных значений. При использовании дополнительных граничных условий, даже если нс треТаблица 7.2

бовать ортогональности невязки к собственной функции, получаются значительно более точные значения собственных чисел, а при выполнении ортогональности невязки они практически совпадают с точными, причем первое и второе собственные числа — с точностью соответственно до десятого и шестого знака после занятой. Этот факт можно объяснить тем, что при совместном использовании точных и приближенных аналитических методов без применения дополнительных граничных условий собственные числа определяются из системы алгебраических линейных уравнений, матрицы которых, являясь заполненными квадратными матрицами с большим разбросом коэффициентов, но абсолютной величине, при большом числе приближений, как правило, оказываются плохо обусловленными. В связи с этим получаемые решения могут существенно отличаться от точных, и особенно при малых значениях числа Фурье.

Главное отличие изложенного выше метода с использованием дополнительных граничных условий состоит в том, что в системе алгебраических линейных уравнений относительно неизвестных коэффициентов С, (г = 0, п) большая часть уравнений разделяется (в одно уравнение входит лишь один неизвестный коэффициент) и, таким образом, легко может быть найдена п) большая часть неизвестных коэффициентов. Относительно оставшихся коэффициентов в общем виде приходится решать лишь два-три алгебраических линейных уравнения, независимо от числа приближений. В результате система алгебраических уравнений при любом числе приближений решается на точном аналитическом уровне. Основную трудность здесь представляет нахождение решения характеристического уравнения относительно собственных чисел краевой задачи, степень которого с увеличением числа приближений возрастает. Математические методы решения таких уравнений разработаны. Ниже (см. параграф 7.2) будет показано, что решениями этих уравнений являются собственные числа краевых задач Штурма—Лиувилля.

Па графиках рис. 7.3 и 7.4 дано изменение невязки г уравнения (7.1) для пяти членов ряда (7.22). Из анализа графиков следует, что при Fo = 0,02 в диапазоне 0 < р < 0,6 уравнение (7.1) удовлетворяется точно. Максималь.

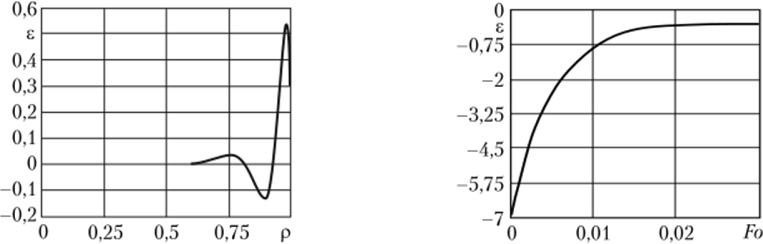
нее. 73. Изменение невязки е Рис. 7.4. Изменение невязки е уравнения (7.1) для Fo = 0,02 уравнения (7.1) для р = 0,9.

ная невязка имеет место вблизи точки р = 1. Невязка уравнения (7.1) в точке р = 0,9 для Fo > 0,02 становится практически равной нулю (см. рис. 7.4).

Максимальная невязка начального условия в = -1 (рис. 7.5) при п = 5 наблюдается в точке р = 1. Это объясняется тем, что в этой точке в любой момент времени выполняется граничное условие первого рода. С увеличением числа приближений невязка начального условия уменьшается, за исключением точки р = 1, где она всегда равна в = -1.

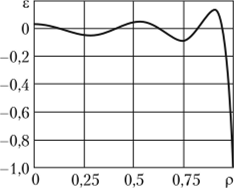
Рис. 75. Изменение невязки в начального условия.