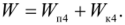Условие равновесия механической системы

В замкнутой системе тел в отсутствие неконсервативных сил полная энергия W = const. Поэтому W_K может увеличиваться только за счет уменьшения W_n.

Если система находится в таком состоянии, что скорости всех тел равны 0, a W_n= ^,_(mjn), то без воздействия извне тела системы нс могут прийти в движение, т. е. система будет находиться в равновесии.

Таким образом, для замкнутой системы равновесной может быть только такая конфигурация тел, которая соответствует минимальной потенциальной энергии системы.

Рассмотрим случай, когда взаимное расположение тел системы может быть определено с помощью только одной величины, например, координаты х. В качестве примера можно привести систему Земля — шарик (модель — материальная точка), скользящий без трения по укрепленной неподвижно изогнутой проволоке (рис. 4.10). На шарик действует консервативная сила — сила тяжести. Так как по условию силой трения пренебрегаем, а сила реакции проволоки, действующая на шарик, перпендикулярна скорости и, следовательно, работы не совершает, поэтому в системе тел выполняется закон сохранения энергии (4.7.6).

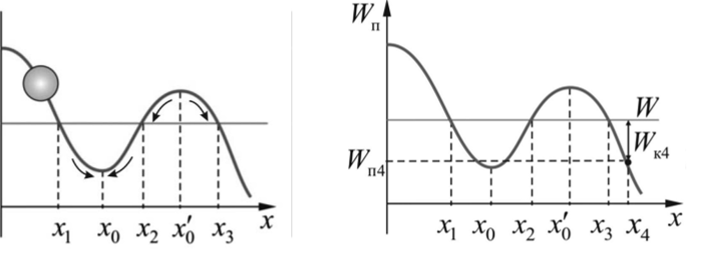
Рис. 4.10 В В В Рис. 4.11

Ш .

Условие минимума потенциальной энергии: — = 0. Согласно.

dv.

(4.6.2), это равнозначно условию:^ =0 (так как потенциальная энергия.

. «ВВ — dW_n d W

является функцией только одной переменной х, то-=-).

дх dv.

Условия равновесия выполняются и для х₀ и для х'₀, но это равновесие неустойчивое (рис. 4.10).

Зная вид функции W_n можно сделать ряд заключений о характере движения любой частицы. Поясним это, воспользовавшись графиком на рис. 4.11. Если полная энергия имеет значение, соответствующее проведенной на графике горизонтальной черте (IV), то частица может совершать движение либо от х, до х₂ либо от х₃ до оо.

На рис. 4.11: область х₂ < х< х₃ — представляет собой потенциальный барьер для движения частицы; область х_{ < х < х₂ — потенциальная яма. Для приведенного на этом рисунке примера имеет место соотношение.