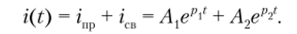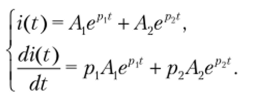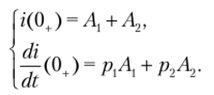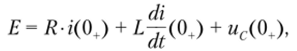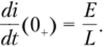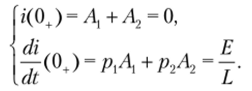Апериодический режим. 
Электротехника, электроника и схемотехника

Когда резистивное сопротивление цепи, изображенной на рис. 8.8, достаточно велико, чтобы удовлетворялось неравенство R > 2^, переходный ток в контуре с учетом формулы (8.9) равен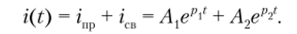

Целью дальнейшего расчета является определение двух неизвестных постоянных Л, и Л₂. Уравнения для них получаем по методике, несколько отличной от применяемой в цепях первого порядка.

1. Наряду с общим видом искомой функции записываем и общий вид ее первой производной по времени:

2. Обе функции времени рассматриваем для первого мгновения после коммутации t = 0₊:

3. Пользуясь уравнениями Кирхгофа для послекоммутационной цепи и законами коммутации, определяем величины г (0₊) и ^(0₊), ^что Д^ает Д^ва уравнения для постоянных Л, и Л₂.

Применительно к цепи, изображенной на рис. 8.8, /(0.) = /(0), так как искомый ток протекает в индуктивности и подчиняется первому закону коммутации. Для определения ^-(0₊) записываем уравнение по второму закону Кирхгофа для момента t = 0₊:

из которого при нулевых начальных условиях, т.с. при г (0₊) = /'(0) = 0 и и_с(0₊) = и_с(0) = 0, получаем.

Тогда для постоянных А_х и Л₂ имеем уравнения.

Их совместное решение дает следующий результат:

Для определенности примем, что в выражении (8.7) (для корней характеристического уравнения) знак «+» принадлежит корню p_v а знак «-» — корню р₂. Тогда абсолютные величины р_{ и р₂ удовлетворяют неравенству Pi I ^< Рг> ^а разностьр_{ — р₂ положительна. Следовательно Л₁ > 0, Л₂ < 0.

При этом положительная экспонента А_{е^р'⁽ затухает медленнее отрицательной экспоненты А₂е^р**. Это отражено на графике (рис. 8.9), где представлены каждая из экспонент, а также их сумма i (t). Таким образом, в апериодическом режиме искомая функция времени i (t) имеет форму всплеска, начинается от нуля и стремится к нулю.

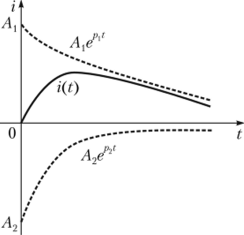
Рис. 8.9. График тока i (t) в цепи, изображенной на рис. 8.8, при R > 2 У L/C (апериодический режим).