Одноразрядные двоичные сумматоры

Как известно, сложение двух чисел, представленных позиционным кодом, как в десятичной, так и в двоичной системах счисления осуществляется поразрядно. Поэтому структурной единицей любого сумматора является одноразрядный сумматор, выполняющий арифметическое сложение цифр одноименных разрядов.

Напомним, что результат сложения двух одноразрядных двоичных чисел в общем случае является числом двухразрядным. По этой причине полный двоичный одноразрядный сумматор имеет два выхода и три входа. Его условное изображение дано на рис. 20.17, а. На входы а, и b_i подаются числа, подлежащие сложению, а на вход р? — цифра, поступающая из предыдущего, более младшего (г — 1)-го разряда при выполнении там операции сложения.

Рис. 20.17. Разновидности сумматоров (условные графические обозначения):

а — полный двоичный одноразрядный сумматор; б — полусумматор; в — четвсртьсумматор Таким образом, одноразрядный сумматор складывает три цифры: а_п b_j, p_i.

Выход 5, предназначен для записи цифры /-го разряда суммы (я + b_t + р7), а выход p_i+x — для записи цифры (/' + 1)-го разряда этой же суммы.

Промышленностью выпускаются также упрощенные варианты одноразрядных двоичных сумматоров, называемые полусумматорами и четвертьсумматорами [1, 12, 13].

Полусумматор, в отличие от полного сумматора, не содержит входа /?, т. е. выполняет суммирование двух чисел без учета результата сложения в предыдущем разряде. Он работает по правилам сложения в самом младшем разряде.

В схеме четвертьсумматора исключены вход /г и выход р_м. На единственном выходе четвертьсумматора записывается только цифра младшего (/-го) разряда суммы (а, + Ъ).

На рис. 20.17, б, в приведены условные графические обозначения полусумматора и четвертьсумматора.

Рассматриваемые функциональные узлы строятся из простейших логических элементов. Методика получения структурной схемы одноразрядного сумматора любой его разновидности традиционна, т. е. включает в себя:

• а) составление таблицы всех возможных состояний на входе и выходе устройства, т. е. таблицы истинности;
• б) запись по составленной таблице алгебраического выражения (логического), связывающего выходную величину с входными;
• в) минимизацию (при необходимости) записанного логического уравнения;
• г) переход от логического уравнения к структурной схеме.

Пользуясь данной методикой, получим структурные схемы, реализующие названые разновидности одноразрядного двоичного сумматора. Начнем с полусумматора, учитывая, что структура четвертьсумматора может быть получена как сто следствие.

Структурная реализация двоичного полусумматора. Все возможные состояния полусумматора представлены в таблице истинности (табл. 20.4). Она даст связь выходных величин S] и p_j+i с входными — я, и Ь_г

Таблица 20.4

Состояния полусумматора.

Пользуясь табл. 20.4, получим алгебраические выражения функций 5,(я₍, bj) и р_;+1(я_;, bj), например, в совершенной дизъюнктивной нормальной форме — СДНФ. Методика перехода от таблицы истинности к алгебраическому уравнению в СДНФ подробно рассмотрена в параграфе 18.3. Согласно ей выделяем в табл. 20.4 строки, где 5, = 1. Это строки 2 и 3. Для каждой выделенной строки записываем логическое произведение из «представителей» набора аргументов я_;, b_t (т.е. либо в не инвертированном виде, либо в виде инверсииД.

• • строка 2: a_j b_j (b_i в данном наборе равно нулю);
• • строка 3: a_i b_j (я_; в этом наборе равно нулю).

Складываем записанные логические произведения и приходим к искомой СДНФ:

Аналогично, но той же методике для р₍._+| из строки 4 табл. 20.4 получаем.

Соотношения (20.13) и (20.14) позволяют построить полусумматор из трех элементов — конъюнкторов (&), выполняющих операции логического умножения «И» (я, Д, яД, яД), и одного дизъюнктора для получения логической суммы («ИЛИ»). Эта реализация показана на рис. 20.18, я.

Очевидно, что для построения четвертьсумматора (рис. 20.18, б) достаточно соотношения (20.13).

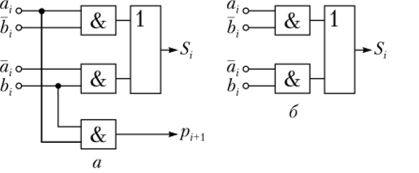
Рис. 20.18. Структурные схемы полусумматора (я) и четвертьсумматора (б).

Структурная реализация полного одноразрядного двоичного сумматора. В табл. 20.5 занесены состояния выходов двоичного одноразрядного сумматора 5_f и p_i+v соответствующие всем возможным ситуациям на его входе.

Таблица 20.5

Состояния полного сумматора.

Согласно табл. 20.5 СДНФ функций 5_;(д, а, />,) и р_м(р, а, 6,) имеют следующий вид:

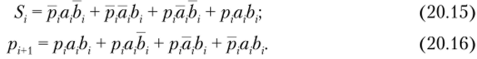
Непосредственное использование соотношений (20.15) и (20.16) при построении сумматора нерационально, так как каждой из функций S,(p_;, а_р Ь_:) иPi+i (Pi> ^ai> bj) потребуется четыре трехвходовых конъюнктора («И») и один дизъюнктор («ИЛИ») на четыре входа. Поэтому целесообразна предварительная минимизация выражений (20.15) и (20.16). Например, несложные преобразования с использованием приема повторения слагаемого в логической сумме (20.16), а также логического тождества х + х = 1 приводят к следующему результату:

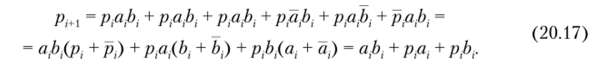
Уравнение (20.17) существенно проще уравнения (20.16).

Логическую функцию (20.15) также можно привести к более простому виду:

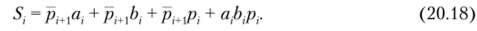
На рис. 20.19, а изображена структурная схема одноразрядного двоичного сумматора, построенная по формулам (20.17) и (20.18). Используемые конъюнкторы (&), за исключением одного, являются двухвходовыми. Схема на рис. 20.19, а также содержит еще и два дизъюнктора — на три и четыре входа.

Полный одноразрядный двоичный сумматор можно построить и на двух полусумматорах. На рис. 20.19, 6 показан один из вариантов такой реализации. Многоразрядные сумматоры строятся на основе одноразрядных.

Рис. 20.19. Структурная схема полного одноразрядного двоичного сумматора (а) и его реализация на двух полусумматорах (6).