Цилиндры гидравлических прессов

Цилиндры являются одними из основных и наиболее ответственных деталей прессов. Гидроцилиндры работают в условиях нагружения, которые зависят не только от условий работы и конструкции самих цилиндров, но и от конструкции сопряженных с ними деталей. Конструкция цилиндра выбирается в зависимости от величины требуемого усилия, условий работы, вида рабочей жидкости и гидравлического давления, под которым она подается в гидроцилиндр. Влияют на конструкцию и технологические возможности предприятия-изготовителя пресса.

Цилиндры бывают поршневые, плунжерные, простые и дифференциальные. Конструкция поршневых цилиндров (рис. 3.4, а) обеспечивает как создание необходимого усилия и рабочее движение поршня 2 с соединенным с ним штоком 3, так и возвратный ход поршня со штоком. Поршень разделяет цилиндр 1 на две полости: поршневую и штоковую. При поступлении рабочей жидкости под давлением р через отверстие I в поршневой полости создается давление. Одновременно штоковая полость II соединяется со сливом. На поршень начинает действовать сила, обеспечивающая рабочее движение поршня со штоком. Возвратный ход поршня и штока происходит после подачи давления рабочей жидкости в штоковую полость через отверстие II и соединения поршневой полости со сливом.

При прямом и возвратном ходе отличаются не только усилия, но и скорости передвижения поршня со штоком. Объясняется это тем, что при одной и той же производительности насоса, подающего рабочую жидкость, объемы поршневой и штоковой полостей отличаются друг от друга.

Рис. 3.4. Схемы гидравлических цилиндров прессов.

Конструкция поршневого цилиндра предусматривает наличие двух видов уплотнений: неподвижного 4 в месте сопряжения цилиндра с подвижным штоком и подвижного 5 в месте сопряжения поршня с цилиндром.

Цилиндры поршневого типа можно подразделить на дифференциальные (рис. 3.4, а) и простые (рис. 3.4, 6). В простых цилиндрах поршень имеет одинаковые скорости прямого и обратного хода и снабжен двухсторонним штоком. В дифференциальных цилиндрах, как было показано выше, поршни развивают различные усилия и скорости при прямом и обратном ходе.

Плунжерные цилиндры (рис. 3.4, в) имеют более простую конструкцию. В них давление рабочей жидкости, поступающей через отверстие I, воспринимается плунжером б, имеющим меньший диаметр, чем внутренний диаметр гидроцилиндра 1. Такая конструкция позволяет существенно упростить обработку внутренней поверхности цилиндра и иметь вместо двух видов уплотнений только один — неподвижное уплотнение 4 в месте сопряжения цилиндра с подвижным плунжером. Существенным недостатком плунжерных цилиндров является отсутствие обратного хода. Для осуществления обратного хода при использовании плунжерных цилиндров приходится устанавливать так называемые возвратные цилиндры (рис. 3.4, г). Основное усилие и ход подвижной плиты 13 осуществляется плунжерным цилиндром 8. Возвратный ход обеспечивается двумя возвратными цилиндрами 7, расположенными симметрично относительно рабочего цилиндра 8. Полость цилиндра 8

соединяется со сливом, а в полости цилиндров 7 под давлением подается рабочая жидкость. Возвратные цилиндры должны преодолевать только силы тяжести и трения, возникающие при движении вверх, поэтому диаметры их плунжеров значительно меньше, чем диаметр плунжера рабочего цилиндра, и, следовательно, при той же самой производительности насоса скорость обратного хода всегда выше, чем рабочего. На прессах разной конструкции устанавливается различное число возвратных цилиндров.

Однако надо иметь в виду, что возвратные цилиндры могут отсутствовать вообще. Так, в прессах нижнего давления с массивными подвижными частями и небольшим возвратным ходом обратное перемещение осуществляется за счет сил тяжести после соединения полости рабочего плунжерного цилиндра со сливом.

При необходимости в прессах используются ступенчатые цилиндры (рис. 3.4, д). В этих цилиндрах реализуется несколько скоростей за счет комбинации дифференциальных поршней с плунжерами. Ускоренное движение происходит при подаче под давлением рабочей жидкости через отверстие I в полость штока 12 поршня 10. Эта полость работает как подвижный гидроцилиндр, в котором размещен неподвижный плунжер 9 — при создании в его полости давления он начинает движение вправо. Благодаря небольшому внутреннему диаметру полости реализуется высокая скорость перемещения штока 12 при сравнительно небольшом усилии. По мере продвижения поршня 10 через отверстие II происходит заполнение поршневой полости цилиндра 11. На конечной стадии передвижения штока 12 необходимо снизить скорость его движения и создать большое усилие. Для этого в поршневой полости гидроцилиндра 11 создается давление рабочей жидкости, скорость движения поршня со штоком снижается, а рабочее усилие возрастает. Для возврата поршня со штоком в первоначальное положение рабочая жидкость под давлением подается через отверстие III в штоковую полость цилиндра 11, а его поршневая полость соединяется со сливом.

Метод расчета цилиндра существенно зависит от способа его крепления к станине пресса. Широко используются крепления цилиндров при помощи буртов или фланцев, изготовленных совместно с цилиндром. Используются фланцы, закрепленные на цилиндре с помощью резьбы или сварки. Применяются конструкции крепления разрезной кольцевой шпонкой. Используется опора цилиндра на его днище.

После выбора давления р_и, с которым будет подаваться в цилиндр рабочая жидкость, необходимо определить диаметр поршня или плунжера, при котором будет развиваться заданное усилие F.

Полученный размер D округляют до ближайшего большего размера по ГОСТ 6540 (табл. 3.2). Затем, в зависимости от принятой конструкции, определяют внутренний диаметр цилиндра, который также должен соответствовать указанному выше стандарту.

Таблица 3.2. Рекомендуемые диаметры поршней, плунжеров и внутренние диаметры гидравлических цилиндров.

При определении толщины стенки цилиндры гидравлических прессов рассчитываются как толстостенные цилиндрические оболочки.

В толстостенных цилиндрах, находящихся под действием внутреннего давления р_п, возникает сложное напряженное состояние, так как одновременно действуют нормальные напряжения в радиальном (о_г) направлении в точке, удаленной на расстояние гот оси цилиндра, в тангенциальном (a_f) и осевом (а_г) направлениях. Величина этих напряжений по теории Ламе для толстостенных осесимметричных сосудов определяется по формулам:

Напряжение, направленное вдоль оси цилиндра о_/( распределено равномерно по толщине стенки (рис. 3.5), а величины напряжений а, и а, по толщине стенки принимают различные значения. Причем на внутренней поверхности цилиндра, то есть при г — R_v напряжения принимают свои наибольшие абсолютные значения.

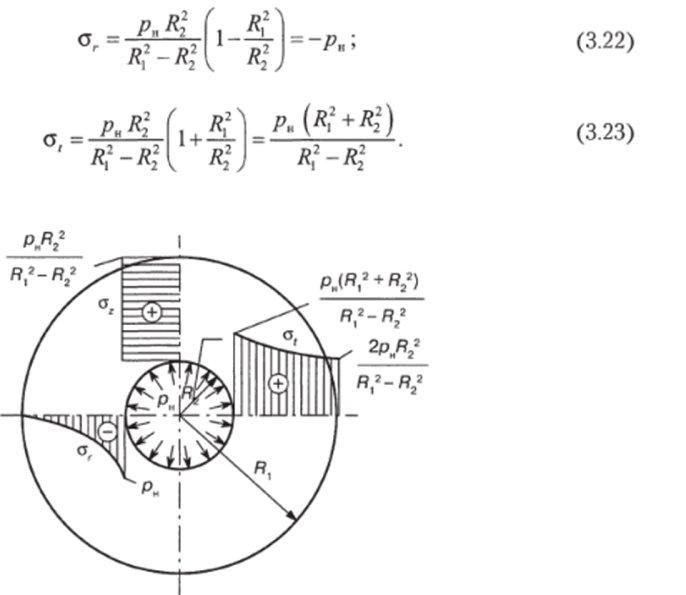
Рис. 3.5. Распределение напряжений в толстостенном цилиндре под действием внутреннего давления.

Напряженное состояние любой из точек, находящихся на внутренней поверхности цилиндра, показано на рис. 3.6.

Рис. 3.6. Напряженное состояние точек, находящихся на внутренней поверхности цилиндра.

Как ранее было указано, в теории сложного напряженного состояния главные напряжения обозначаются а, а₂, с₃, причем а,? о₂> а₃. Таким образом, в наиболее нагруженных точках цилиндра главные напряжения принимают следующие значения: о, — а,; а₂ — а,; а₃ — а_г.

Для определения эквивалентного напряжения в стенках цилиндра, выполненного из пластичного материала (обычно из стали), могут быть использованы гипотеза максимальных касательных напряжений (III гипотеза прочности) и энергетическая гипотеза формоизменения (IV гипотеза прочности). Достоверность расчетов на основе обеих этих гипотез примерно одинакова. Однако в полимерном машиностроении большее применение получили расчеты на основе энергетической гипотезы прочности: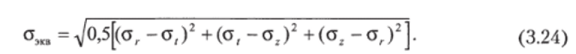

Условие прочности а_экв? [о], где [а] — допускаемое напряжение при растяжении:

где а_г — предел текучести при рабочей температуре материала стенки цилиндра; п — коэффициент запаса прочности.

После подстановки в (3.24) соответствующих значений из (3.21)—(3.23), а также замены /?, — 0.5D, иЛ₂^и 0,5D₂ получим.

С учетом (3.26) минимальная толщина стенки цилиндра 6 может быть рассчитана по формуле.

где с — припуск на обработку цилиндра при ремонте (в большинстве конструкций гидравлических прессов проточка цилиндров при ремонте не производится, и величина с принимается равной нулю).

В прессах достаточно часто используются конструкции, при которых гидравлический цилиндр опирается на свое днище. В случае работы с простым, не дифференциальным плунжером в стенках цилиндра, опирающегося на дно, отсутствуют осевые напряжения, т. с. с_г = 0.

В дифференциальных плунжерах в стенке цилиндра возникает осевое усилие. Величина этого усилия зависит от площади дифференциальной полости и величины давления находящейся в ней рабочей жидкости (р_и). В большинстве случаев при расчете цилиндров с дифференциальным плунжером, опирающихся па днище, величиной осевых напряжений можно пренебречь.

В этом случае формула для определения наружного диаметра будет иметь вид.

На рис. 3.7 показано изменение отношения D_{/D₂ — К, характеризующее металлоемкость конструкции в зависимости от соотношения [.

Рис. 3.7. Изменение значения К в зависимости от [о]/р_н.

Как показывает практика, оптимальное давление р^ с точки зрения экономии материала (получения минимального наружного диаметра) для цилиндра, опирающегося на фланец, равно: р_овт — 0,289[а], а при опоре цилиндра на днор_т — 0,277[а].

В расчетах коэффициент запаса прочности для кованых стальных цилиндров принимается п — 2,65−2,9, а для литых п — 3,0−3,5. При этом допускаемые напряжения будут равны: сталь 35 [ст] = 100−120 МПа; сталь 45 [а] = 125−135 МПа; сталь 35Л [о] = 80−95 МПа.

При конструировании цилиндров следует, но возможности, избегать резких переходов и утолщений стенок, так как в этих местах происходит концентрация напряжений, и появляются дополнительные перерезывающие силы, вызванные разной величиной деформаций в радиальном направлении.

Опорный фланец цилиндра, передающий усилие от цилиндра на станину пресса (архитрав), обычно изготавливается заодно с цилиндром. В отдельных случаях применяется сварка. В связи с возможными внутренними напряжениями, вызванными неравномерным нагревом и короблением окончательная механическая обработка должна производиться после сварки.

Применяется также крепление цилиндров при помощи разрезных колец, являющихся по существу кольцевой составной (разрезной) шпонкой.

При приближенном расчете утолщенную часть цилиндров в области перехода во фланец делают несколько большей толщины. Переход от цилиндрической части к поверхности фланца скругляется радиусом г_п — (0,15−0,25)*, где * — толщина плоского донышка. Приближенно толщина плоского донышка цилиндра может определяться следующим образом t = (1,5—-2,5)6, где 6 — толщина стенки цилиндра.

Наружный диаметр фланца О_ф определяется из допустимого напряжения на смятие [c]_CM опорных поверхностей фланца и верхней поперечины.

Завышать наружный диаметр фланца против расчетного не следует, с тем, чтобы упругая деформация фланца в радиальном направлении была близка к деформации цилиндра.

Высота фланца h принимается в зависимости от толщины стенки цилиндра б, равной

Переход между цилиндром и фланцем выполняют с радиусом скругления г -(0,15−0,25)/*.

Толщина плоского днища цилиндра 6_д определяется по формуле.

где (р — коэффициент, учитывающий ослабление сечения днища отверстиями, например, для подвода и отвода рабочей жидкости.

Этот коэффициент либо может быть принят из эмпирического соотношения (ф = 0,7+0,8), либо рассчитан по формуле.

где 1C — сумма диаметров отверстий в днище, расположенных по диаметральному сечению.

Как видно из (3.33), при отсутствии отверстий в днище ф = 1.

Приближенно толщина плоского днища цилиндра может определяться по формуле 8_д — (1,5−2,5)5. Переход от цилиндрической части к плоскому днищу рекомендуют выполнять с радиусом г_п — 0,25D₂, но не меньше 30 мм.

Сферические днища выполняются с радиусом сферы /?_сф — (1−2)/?₂ и переходом от цилиндра к сфере с радиусом г_ф — 0,4Я₂. Толщина сферического днища составляет обычно 5_д — (1 -1,3)6.

Полную глубину цилиндра L можно определить по формуле.

где II — ход плунжера; /, и /₂ — ширина проточек под направляющую втулку и уплотнение; /₃ — глубина сферической части цилиндра.

Ход II в соответствии с ГОСТ 6540 определяется из конструктивных соображений из нормального ряда, приведенного в табл. 3.3.

Крышки гидравлических цилиндров выполняются плоскими. Такие крышки, установленные на винтах или шпильках, рассчитывают как круглые пластины с заделкой по наружному контуру D_hk, нагруженные равномерно распределенной нагрузкой по внутреннему диаметру гидроцилиндра D_r

Для отношения D_xJD<~3,13 наибольшее напряжение в опасном сечении крышки определяется по формуле.

где ф_я — коэффициент, зависящий от DJD₂; 6_к — толщина крышки.

Таблица 3.3. Рекомендуемый максимальный ход поршней и плунжеров.

Таблица 3.3, окончание.

Для отношения D_m/D₂ > 3,13 наибольшее напряжение в опасном сечении крышки определяется по формуле

где ф_А — коэффициент, зависящий от D_HK/D_r

Коэффициенты <�р_в и <�р_/( могут быть определены из графика, приведенного на рис. 3.8.

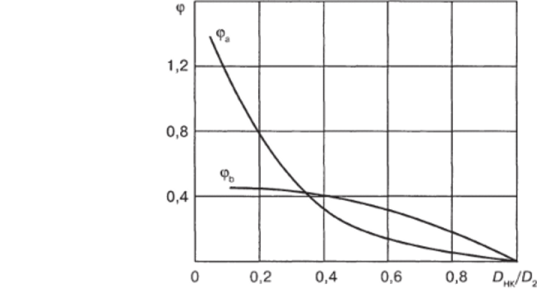
Рис. 3.8. Графики зависимости <�р₄ и ф_й от DJD₇

Крышка, устанавливаемая на упругой прокладке, проверяется на изгиб в двух сечениях: в диаметральной плоскости, проходящей через отверстия крепления, и по кольцевому сечению, совпадающему со средним диаметром уплотнения.

Напряжение изгиба в диаметральном сечении равно.

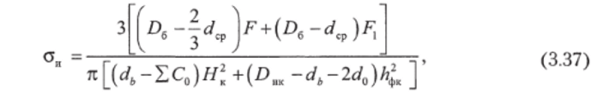
где F— усилие от гидростатического давления среды на крышку; F_t — добавочное усилие, передающееся на уплотнительное кольцо; D₆ — диаметр окружности расположения болтов; ^_ср — средний диаметр уплотнительного кольца; А_фк — толщина фланца крышки; Н_к — толщина крышки; D_M — наружный диаметр крышки; 1С₀ — сумма диаметров отверстий в крышке, расположенных в расчетном сечении; d_b — диаметр посадочного бурта крышки; d₀ — диаметр отверстий крепления.

Для разгрузки болтов, крепящих гидроцилиндр к плитам или другим деталям пресса, цилиндр 1 (рис. 3.9) часто выполняется с буртом, упирающимся в плиту 2. В пограничной зоне между стенкой цилиндра и буртом при работе цилиндра возникает сложное напряженное состояние, усугубляющееся концентрацией напряжений, величина которых зависит от радиуса R. В целях уменьшения концентрации напряжений рекомендуется, чтобы R * (0,15−0,20)5.

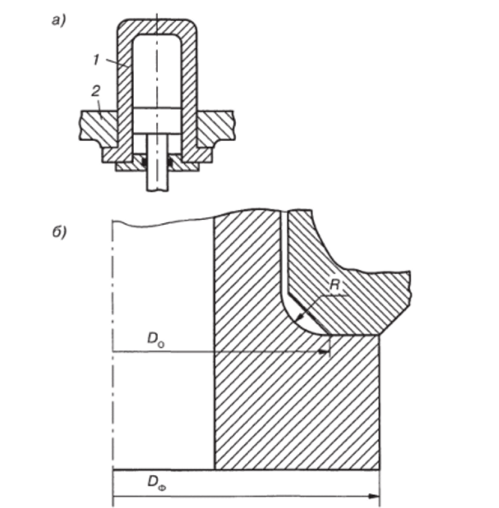
Рис. 3.9. Схема опорного бурта гидроцилиндра: а — схема цилиндра; б — место соединения ци линдра и плиты Опорный бурт цилиндра проверяется на смятие:

Допускаемое напряжение на смятие принимается [а]_см — 80−100 МПа.

Расчет деталей уплотнений цилиндров, естественно, зависит от их конструкции. Плунжеры и штоки гидравлических цилиндров большого диаметра чаще всего имеют уплотнение, аналогичное показанному на рис. 3.10, а. Это уплотнение состоит из пакета манжет 1, нажимной втулки 2, нажимного фланца 3 и шпильки 4. Часто нажимные фланцы 5 (рис. 3.10, б) изготавливают заодно с фланцем и снабжают буртиком для крепления втулки в. Втулки 2 и 6 выполняют обычно из бронзы или антифрикционного чугуна, нажимные фланцы 3 и 5 — из сталей 35 и 45, а шпильки 4 — из сталей 40Х или 40ХН.

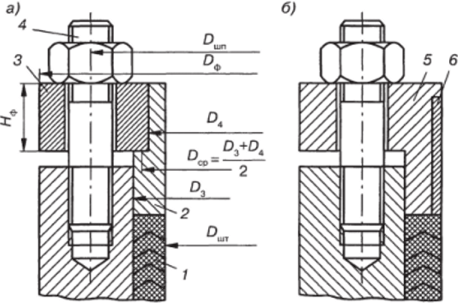
Рис. 3.10. Детали уплотнений гидроцилиндров.

Для описанной конструкции уплотнения усилие, действующее на шпильку, можно представить как-

где (р — коэффициент, принимаемый для шевронных уплотнений, равен 0,785. Напряжение в шпильке.

где 5_ШП — площадь сечения шпильки по внутреннему диаметру; п — число шпилек.

Допускаемое напряжение для шпилек из сталей 40Х или 40ХН, подвергнутых термообработке в режиме улучшения, равно [о]_р = 140 МПа, а из сталей 35 и 45 — соответственно [а]^ - 90 МПа и [о]^ = 100 МПа.

Фланцы уплотнительных устройств рассчитываются с учетом возможной перетяжки гаек, и усилие, действующее на фланец, определяется как.

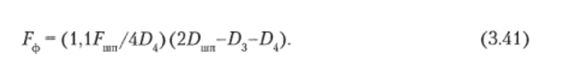
Напряжение на внутренней поверхности фланца определяется по формулам:

• для свободного фланца (рис. 3.10, а)

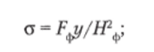
• для фланца со втулкой (рис. 3.10, б)

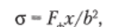
ч* •.

где у — постоянный коэффициент для свободного фланца; х— постоянный коэффициент для фланца со втулкой; b = (D₃-D_m)/2 — толщина фланца с втулкой.

Для стальных фланцев коэффициенты у их вычисляются по формулам.

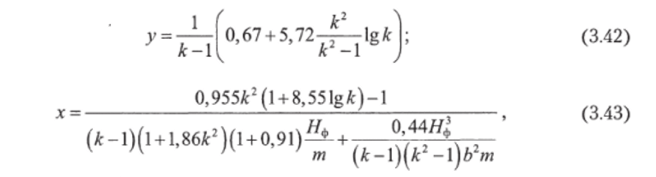
где k «D^/D^, т = >/D₄6.

Вычисленные напряжения не должны превышать допускаемые, значения которых приведены в табл. 3.4.

Таблица 3.4. Допускаемые напряжения во фланцах, МПа.

Нажимные втулки должны проверяться на смятие по поверхности соприкосновения с фланцем (рис. 3.10, а):

Допускаемое напряжение на смятие для бронзы и антифрикционного чугуна [оJ = 80 МПа.

При расчете на прочность поршневого штока (рис. 3.11) его предварительные размеры рекомендуется определить из следующих соображений:

• наружный диаметр резьбы d — по стандартам на метрические резьбы;

• • посадочный диаметр под поршень d₂— d + (2−6) мм;
• • диаметр выточки под резьбу d₃ = d_x- (0,5−1,5) мм;
• • диаметр хвостовика — d_x- (3−6) мм;
• • рабочий диаметр г/. = d₂ + (5−10) мм, а затем округляется в большую сторону до размера, рекомендуемого по ГОСТ 6540 (табл. 3.5).

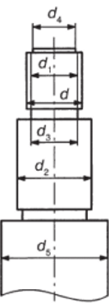
Рис. 3.11. Схема хвостовика штока

Таблица 3.5. Рекомендуемые диаметры штоков гидравлических цилиндров.

Таблица 3.5, окончание.

Для изготовления штоков поршней часто используются стали 20,35 и 45. Резьбовое соединение штока в процессе реверсирования поршня испытывает знакопеременную нагрузку. Резьбовая часть штока испытывает нагрузку под действием: F — внешнего усилия, развиваемого гидростатическим давлением, которое растягивает и сжимает шток; Т— усилия от предварительной затяжки гайки; F — добавочного переменного усилия, возникающего в соединении под действием усилия F М — крутящего момента, возникающего вследствие трения в резьбе.

Наименьшее усилие от предварительной затяжки.

где F_H — номинальное усилие, создаваемое цилиндром; С₂ — жесткость ступицы поршня; С, — жесткость хвостовика штока.

Жесткость ступицы поршня (рис. 3.12) определяется по формуле.

где Е₂ — модуль упругости первого рода материала поршня; S₂ * n (dJ-(P₂)/4.

Рис. 3.12. Схема соединения поршня и штока.

Жесткость хвостовика штока определяется из уравнения суммарной податливости:

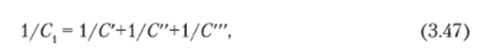
где С — жесткость участка хвостовика диаметром d₂ С" — то же диаметром d₃; С" — то же диаметром d₆. Жесткость каждого элемента определяется по формуле.

где 5 — nd/A Е_х — модуль упругости первого рода материала штока.

Усилие предварительной затяжки Т> T_min и определяется по формуле.

где k = (1,2−1,3).

Переменное растягивающее хвостовик усилие F₂, возникающее под действием внешнего усилия F, создаваемого гидростатическим давлением, определяется по формуле

Так как внешнее усилие F изменяется в пределах одного цикла от F — F_n до.

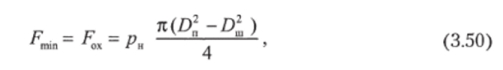
где F_m — усилие, развиваемое цилиндром при обратном ходе поршня; D_n — диаметр поршня; D_m — диаметр штока; р_и — давление рабочей жидкости, то из уравнения (3.49).

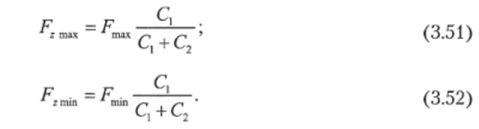
Крутящий момент от затяжки гайки.

где d — наружный диаметр резьбы; р — коэффициент, величина которого определяется по табл. 3.6.

Номинальные напряжения от растяжения по внутреннему диаметру резьбы определяются по формулам

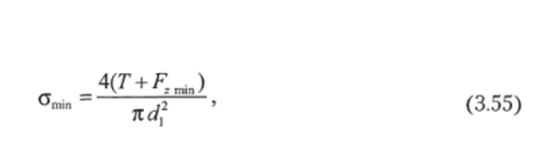
где d_x — внутренний диаметр резьбы.

Таблица 3.6. Значения коэффициента [S.

Любой цикл может быть представлен как результат наложения постоянного напряжения а_т на напряжение, меняющееся по симметричному циклу с амплитудой о_а. Среднее напряжение цикла о_т равно Амплитуда цикла о_а

Кроме того, поршневой шток находится под действием постоянного крутящего момента М_кр. Номинальное касательное напряжение.

где W — 1иР/16 — полярный момент сопротивления сечения вала.

Коэффициент запаса усталостной прочности определяется, но эмпирической формуле Гафа и Полларда

где п_с — запас усталостной прочности в предположении, что касательные напряжения х отсутствуют; п. — запас по касательным напряжениям, установленный в предположении, что, а — 0.

Коэффициент запаса усталостной прочности п_с в данном случае следует определять по пределу усталости.

где а, — предел выносливости (предел усталости) при растяжении с симметричным циклом; (K_g)_D — эффективный коэффициент концентрации напряжений для резьбы штока при растяжении.

Коэффициент (К_а)_п зависит от вида резьбы, характеризуемого отношением радиуса закругления впадины к высоте резьбы, предела прочности при растяжении и наружного диаметра резьбы:

где К_а — эффективный коэффициент концентрации напряжений для углеродистой стали с пределом прочности а_в = 400 МПа при наружном диаметре резьбы 12 мм (К_а для трапецеидальной резьбы определяется по графику на рис. 3.13, отношение r/h для метрической резьбы равно 0,266);? — поправка на величину предела прочности материала штока, которая определяется по графику на рис. 3.14; е_о — коэффициент влияния абсолютных размеров (определяется по графику на рис. 3.15).

Коэффициент запаса усталостной прочности п_г в данном случае следует определять, но пределу текучести

где т_т — предел текучести материала штока при кручении.

Запас прочности п для штоков должен быть не менее 1,3−1,5.

Рис. 3.13. Зависимость коэффициента концентрации напряжений К_о от отношения r/h Рис. 3.14. График для определения поправки на величину предела прочности.

Рис. 3.15. График для определения коэффициента^.

Так как длина штока всегда значительно больше его диаметра, то рекомендуется его проверка на устойчивость при продольном изгибе. Коэффициент запас устойчивости п_у определяется отношением

где F — критическое усилие, вызывающее потерю устойчивости; F — номинальное усилие, развиваемое цилиндром.

Критическое усилие для сжатия стержней постоянного сечения определяется по формуле Эйлера:

-г.

где/ = 7се/‘₅/64 — осевой момент инерции поперечного сечения рабочей части штока; / — длина сжимаемой части штока; р — коэффициент приведения длины, зависящий от способа закрепления концов штока, его значение выбирается по рис. 3.16, а -г.

Рис. 3.16. Зависимость коэффициента приведенной длины р от способа закрепления концов штока.

Критическое напряжение определяется по формуле.

где гибкость штока X — p//i, i — dj4 — радиус инерции поперечного сечения рабочей части штока.

Формулой Эйлера можно пользоваться, пока применим закон Гука. Она справедлива, когда где с_п — предел пропорциональности.

Для СтЗ предельная гибкость X равна 100.

При гибкости штока, меньшей Х_прсд, формула Эйлера неприменима. Для таких штоков расчет на устойчивость производится по формуле.

где [F — допускаемое усилие; <�р — коэффициент понижения допускаемого напряжения, зависящий от гибкости X и материала штока; [а]^ — допускаемое напряжение на сжатие.

Значение коэффициента <�р определяется по табл. 3.7. Запас устойчивости я. для штоков должен быть не менее 2,5−4,0.

Таблица 3.7. Значения коэффициента понижения допускаемого напряжения <�р

Плунжер гидравлического пресса передает усилие, создаваемое рабочей жидкостью, на подвижную плиту и пресс-инструмент. Принципиально различают две конструкции плунжеров: до диаметра -200 мм они имеют сплошное поперечное сечение, а плунжеры больших диаметров, как правило, выполняют пустотелыми. Плунжеры изготовляются из чугуна марки СЧ 21−40, стального литья марки 35Л и углеродистых сталей марок 35 и 45 (прокат).

Полыми или пустотелыми плунжеры больших диаметров изготовляют для уменьшения их веса. Плунжер, показанный на рис. 3.17, а работает на внешнее давление и может изготавливаться как из чугуна, так и из стали.

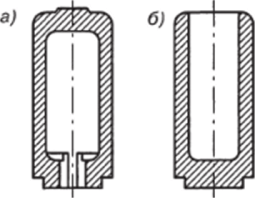
Рис. 3.17. Полые плунжеры: а — открытый наружу: б — открытый во внутрь цилиндра Полые плунжеры, открытые внутрь цилиндра (рис. 3.17, б), рассчитываются так же, как цилиндры при опоре на днище. Такие плунжеры изготавливаются из стали, кованными или литыми.

Длина плунжера назначается с таким расчетом, чтобы при одном из крайних положений плунжер, опираясь на днище цилиндра, не давал подвижной плите касаться уплотнительных элементов. В другом крайнем положении перемещение плунжера, а вместе с ним и подвижной плиты пресса, должно ограничиваться механическими упорами так, чтобы плунжер не вышел из направляющей втулки.

Сплошные плунжеры рассчитываются на сжатие и устойчивость аналогично расчету штоков поршней. Плунжеры с отношением длины / к диаметру d меньше десяти (l/d <10) на устойчивость не проверяются. Пустотелые плунжеры, открытые наружу, рассчитываются по аналогии с толстостенными цилиндрами, с той разницей, что гидростатическое давление действует извне.

В толстостенных цилиндрах, находящихся под действием внешнего давления р_н, возникает сложное напряженное состояние. Величины радиального (о), тангенциального (а₍) и осевого (а₇) напряжений в точке, удаленной на расстояние гот оси цилиндра, согласно теории Ламе для толстостенных осесимметричных сосудов, определяется по формулам.

Распределение напряжений в толстостенных сосудах под действием внешнего давления показано на рис 3.18.

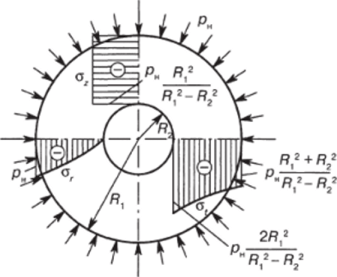
Рис. 3.18. Распределение напряжений в стенке плунжера под действием внешнего давления.

Опасной является (как и при нагружении внутренним давлением) внутренняя поверхность плунжера. При г — R₇ напряжения принимают свои наибольшие абсолютные значения:

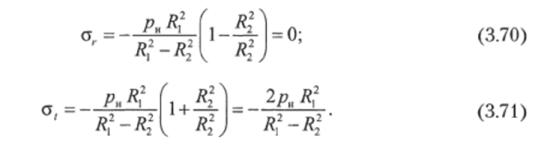
Таким образом, в наиболее нагруженных точках плунжера главные напряжения принимают следующие значения:

При расчете по энергетической гипотезе прочности после подстановки этих значений <5₍, а, <5_г в формулу (3.24) и соответствующих преобразований получим расчетную формулу для внутреннего радиуса плунжера:

Плунжеры, открытые вовнутрь цилиндра (рис. 3.17, 6), испытывают воздействие гидростатического давления изнутри и снаружи и расчетам не подвергаются. При необходимости в прессах используются ступенчатые цилиндры (рис. 3.4, д).