Алгоритм Кудрявцева голосования по тестам

Пусть {1,2,…, п} — множество признаков. Договоримся подмножество т с {1,2, …, п} обозначать булевским вектором t = (?i,…,?_n), подразумевая, что признак г € т точно тогда, когда U = 1.

Пусть как и ранее Т = {а, = (а_я,…, a_jn) :j = 1,2 ,…, 774},.

Т2 = {6^ = (6jfi,… _tbj_n): j = 1,2,.*., 7712} — множества элементов обучающей выборки, принадлежащие классам К и К_2 соответственно.

Обозначим Т = Т (Т, Т2) —* опорное множество тестов для обучающей выборки 7i, 7a. В качестве опорного множества Т ' могут выступать, например, множество всех тестов, множество тупиковых тестов, или множество тестов фиксированной длины.

Если а = (ai,…, o_n) — элемент обучающей выборки, t = ($ 1/…,?_п) € Т — некоторый тест, а х = (х_ь…, х_п) — объект, подлежащий классификации, то скажем, что mecm t голосует за элемент, а на объекте х, если.

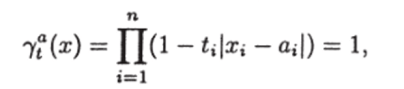
т.е. на признаках из теста t объекты, а и х совпадают.

Тогда сумму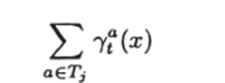

можно интерпретировать как интеграл голосования множества Tj, j = 1,2, а многочлен

есть интегральный голос всего опорного множества тестов Т за класс Kj₉ j = 1,2.

Многочлен R (x) = Гг (х) — Ti (x) называется многочленом голосования.

Алгоритм голосования по тестам, предложенный В. Б. Кудрявцевым, состоит в том, что на объекте х, подлежащем классификации, вычисляется многочлен голосования R (x), и если Л (х) < 0, то х относится к классу^, ик классу К2 — в противном случае.

Рассмотрим многочлен ri (x). Раскрывая скобки в произведениях, получим.

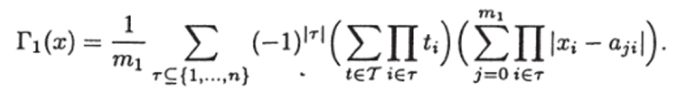
Возьмем линейную часть этого многочлена по переменным.

Zji = |xi — dj’ij:

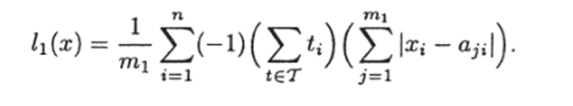
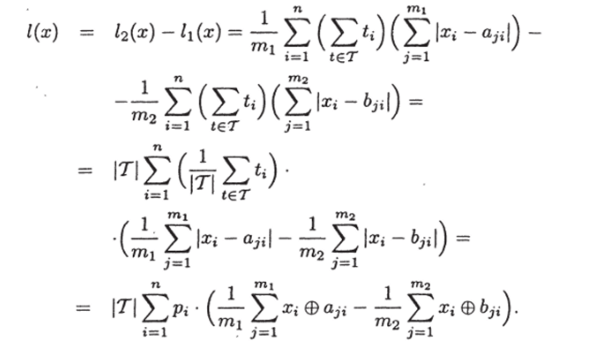
Сравнивая полученное с (1.4) и (1.5), можем заметить, что известный алгоритм Л является линейным приближением многочлена голосования.

Алгоритм голосования по тестам предполагает умение перечислять все тупиковые тесты. В работах [3, 5, 15, 16] приводятся асимптотически оптимальные алгоритмы перечисления всех тестов.

В работе [20] показано, что если в качестве опорного множества брать множество «коротких» тестов (тестов, мощность которых порядка logn), то алгоритм голосования становится не только значительно менее трудоемким, но и более надежным.

С помощью тестовых алгоритмов были успешно решены многие практические задачи распознавания, в частности геологические задачи по оценке запасов руды и подобные им [26, 28, 29, 34, 64].

Так, исследование ртутных месторождений позволило дать практические рекомендации о необходимости постановки геолого-разведочных работ по некоторым малоизученным месторождениям Северо-востока СССР; по материалам Приморского геологического управления о месторождениях олова Приморья были получены высокие оценки масштабов оруднения некоторых малоизученных месторождений, что в дальнейшем подтвердилось при проверке разведывательными работами. На двух месторождениях (Южном и Смирновском) было установлено, что рудные тела, сравнительно бедные оловом на поверхности, на глубине переходят в богатые руды с высоким содержанием оловянного камня.