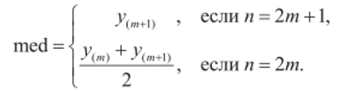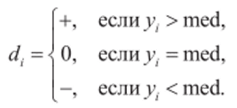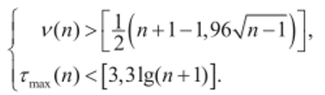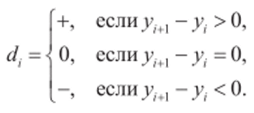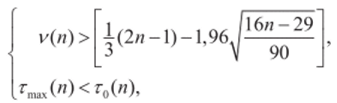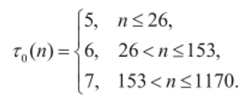Критерий серий, основанный на медиане выборки

Гипотеза случайности согласно этому критерию проверяется следующим образом:

• 1) Элементы исходного ряда располагаются в порядке возрастания, т. с. из исходного ряда y_vy₂,'••?>}>" образуется ранжированный (вариационный) ряд.
• 2) Определяется медиана ранжированного ряда:

3) Сравнивая значения исходного ряда y_l9i = ₉n с медианой, составляется последовательность d_l, d_2i…, d_n по правилу.

В дальнейшем рассматриваются только плюсы и минусы, нули не участвуют в анализе.

• 4) Подсчитывается число серий v (ri) в последовательности </,/ = 1,…, и. Под серией понимается последовательность подряд идущих плюсов или минусов. Один отдельно стоящий плюс или минус тоже считается серией.
• 5) Определяется (п) — протяженность самой длинной серии.
• 6) При условии случайности ряда у₁₉у₂«««чУ_я (т. ^с— ^в отсутствии тенденции) протяженность самой длинной серии не должна быть слишком большой, а общее число серий — слишком маленьким. Поэтому, если нарушается хотя бы одно из следующих неравенств, гипотеза о случайности отвергается приблизительно для 5%-ного уровня значимости:

Здесь с помощью квадратных скобок [•] обозначена целая часть числа. Если оба неравенства выполнены, то гипотеза случайности принимается.

КРИТЕРИЙ «ВОСХОДЯЩИХ И НИСХОДЯЩИХ» СЕРИЙ

Согласно этому критерию гипотеза случайности проверяется следующим образом:

1) для исходного ряда у₁₉у₂," ;У" образуется последовательность </,d₂,.с/_я_, по следующему правилу:

В дальнейшем рассматриваются только плюсы и минусы, нули не участвуют в анализе;

• 2) подсчитывается v (n) — число серий в последовательности d_i9i = ,…, n—1. Под серией понимается последовательность подряд идущих плюсов или минусов. Один отдельно стоящий плюс или минус тоже считается серией;
• 3) определяется г_1Шд.(л) — протяженность самой длинной серии;
• 4) в условиях случайности временного ряда число серий нс должно быть слишком маленьким, а протяженность самой длинной серии — слишком большой. Если нарушается хотя бы одно из следующих двух неравенств, то гипотеза случайности отвергается для приблизительно 5%-ного уровня значимости:

где.

Если оба неравенства выполнены, то гипотеза случайности принимается.