Основные параметры ударной волны

Для количественной характеристики ударной волны надо определить следующие величины (параметры): скорость распространения ударной волны, скорость движения потока среды, давление, плотность и температуру возмущенной среды. Приводимые ниже соображения в принципе справедливы не только для газов, но и для конденсированных сплошных сред. Рассмотрим (рис. 1.4) грубу с поперечным сечением 1 см², заполненную покоящимся газом, давление которого ро и плотность роВ трубу вдвигается поршень с постоянной скоростью U.

Если бы в трубе находилось несжимаемое вещество, то внезапное движение поршня мгновенно передалось бы всей массе вещества, заполняющей трубу. В сжимаемом же газе возбуждение, вызванное движением поршня, передается с конечной скоростью, поэтому впереди поршня образуется конечная зона газа, сжатого до давления р и плотности р. При движении системы «поршеньсжатый газ» все новые массы невозмущенного газа сжимаются до давления р и плотности р и приобретают скорость U, вследствие чего зона сжатого газа непрерывно увеличивается.

Граница этой зоны (плотность АА на рис. 1.4) перемещается вдоль трубы с некоторой скоростью D.

Справа от АА — неподвижный газ с начальными параметрами (давление ро, плотность ро, температура Го), слева — газ, сжатый до давления р с плотностью р и движущийся со скоростью поршня U. На границе раздела (фактически представляющей собой не плоскость, а некоторую область конечной, хотя и весьма малой ширины), называемой фронтом ударной волны, значения параметров, характеризующих состояние газа, изменяются очень резко, скачкообразно.

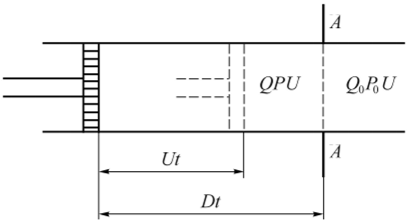
Рис. 1.4. Схема образования ударной волны в трубе движением поршня.

Если сжатие газа происходит настолько быстро, что можно пренебречь потерями энерг ии за счет теплопроводности, и если не учитывать внутреннее трение в газе и трение между движущимся газом и поверхностью трубы, то легко получить уравнения, связывающие параметры ударной волны. Для этой цели используем основные законы механики и термодинамики:

• 1) уравнение сохранения массы (уравнение неразрывности);
• 2) уравнение сохранения импульсов;
• 3) уравнение сохранения энергии;
• 4) уравнение состояния газа.

Уравнение сохранения массы. За время t г раница АА (рис. 1.4) уйдет от начального положения поршня на расстояние Dt. Масса вещества, которая подвергалась сжатию за это время, равна poDl. Она равна массе газа, сжатого до плотности р, между поршнем, продвинувшимся на расстояние Ut, и плотностью АА:

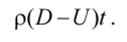
По закону сохранения массы запишем: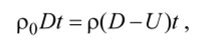

ИЛИ.

Уравнение сохранения импульсов. Указанная масса вещества приобрела скорость, равную скорости движения поршня U.

Импульс, приобретенный массой газа, заключенной между поршнем и фронтом волны за время t, равен р_QDtU. Этот импульс равен импульсу сил давления за эго же время (рp₀)t. Поэтому.

или.

Уравнение сохранения энергии. Приращение энергии вещества при сжатии равно работе внешней силы, перемещающей поршень за время 1.

При давлении р на поршень, прошедший путь Ut, работа внешней силы равна pUt. Приращение энергии для единицы массы газа равно.

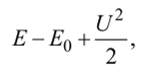
где Е — Ео — приращение внутренней энергии;

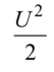 — приращение кинетической энергии единицы массы вещества.

Для массы газа р₀Dt, подвергшейся сжатию, приращение энергии составит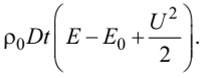

По закону сохранения энергии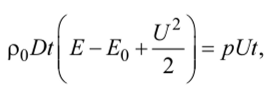

ИЛИ.

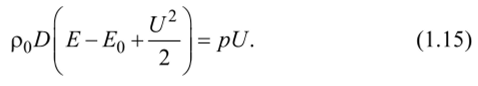
Общие соотношения для ударных волн. Адиабата Погонно. Преобразуем полученные уравнения. Уравнение (1.13) можно представить в виде.

Так как при сжатии газа р>р₀, то из (1.16) непосредственно следует, что D и U направлены в одну сторону, причем D > U. Определим D и U

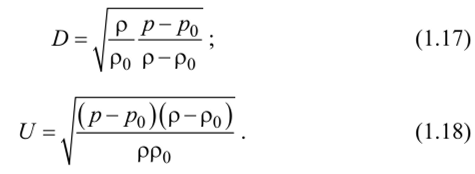
После простых преобразований получим 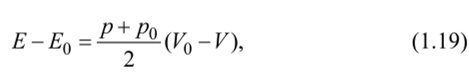где 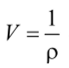 — удельный объем.

Этому уравнению, показывающему, какие состояния могут получиться из данного начального состояния (ро^о) однократным сжатием при переходе через фронт ударной волны, соответствует в плоскости (р, V) кривая, называемая адиабатой Гюгонио.

Адиабата Погонно для идеального газа. Считая, что для вещества, сжатого в волне, справедливо уравнение состояния идеального газа, можно записать:

Как известно, для идеального газа с постоянной теплоемкостью.

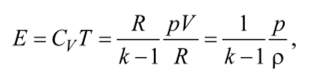
где R — газовая постоянная;

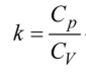 — отношение теплоемкостей, следовательно,.

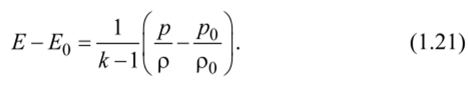
Подставляя значение E-Eq из уравнения (1.21) в уравнение (1.19), получим.

Таким образом, даже при неограниченном росте давления в ударной волне плотность газа сохраняет конечное значение. Это обстоятельство существенно отличает ударное сжатие от обратимого сжатия, например, по закону изоэнтропы (адиабаты Пуассона).

Из уравнения (1.22) можно также видеть, что сжатие в ударной волне необратимо. Так, если из одного и того же начального состояния (/?оРо)газ сжимается в ударной волне в одном случае сразу до давления р, а в другом — сначала до некоторого давления р'{р <�р' <�р), а затем второй ударной волной до того же давления р, то конечные состояния сжатого газа будут различны.