Спектральное представление непериодических сигналов с помощью преобразований Фурье

Метод рядов Фурье допускает определенное обобщение, позволяющее получать спектральные характеристики и непериодических сигналов.

Преобразование Фурье (Fourier transform) является инструментом спектрального анализа непериодических (импульсных) сигналов (их еще называют финитными, т. е. пространственно ограниченными). Такие сигналы отличны от нуля только на ограниченном интервале времени. Очевидно, что импульсный сигнал будет иметь и конечную энергию — если только он не содержит разрывов второго рода (с уходящими в бесконечность ветвями функции).

Для иллюстрации перехода от ряда к интегральному преобразованию Фурье применяют пе вполне строгий математически, по зато понятный аналитический подход. В теории спектрального представления непериодических импульсных сигналов используют искусственный прием, формально (мысленно) заменяя одиночные сигналы периодическими с бесконечно большим периодом следования Т —*? ⁰⁰ (рис. 2.17). Положим, что некая функция u (t) аналитически описывает одиночный импульсный сигнал ко;

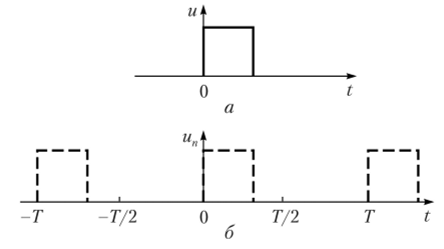
Рис. 2.17. Непериодические сигналы:

а — одиночный импульс; б — условное периодическое представление нечной длительности (рис. 2.17, а). Мысленно дополнив его такими же импульсными сигналами, следующими с некоторым интервалом Т (штриховые импульсы на рис. 2.17,6), получим периодическую последовательность аналогичных импульсов u_n(t) = u (t ± пТ).

Для того чтобы вне искусственно введенного интервала времени [О, Т| исходный сигнал был равен нулю, необходимо увеличить период повторения этих импульсов. В пределе, при увеличении длительности периода и Т —?оо, все импульсы уйдут вправо и влево в бесконечность и периодическая последовательность импульсов u_n(t) вновь станет одиночным импульсом u (t). В этом случае выражения (2.20) и (2.21) сохраняют смысл. Подставив соотношение (2.21) в формулу (2.20), запишем периодическую функцию.

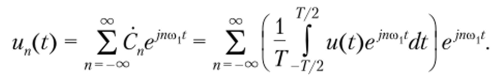
Так как период следования импульсов Т= 2тс/со^ то.

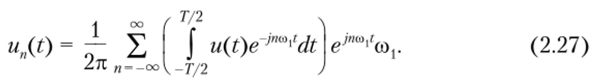
Нетрудно заметить, что при увеличении периода следования импульсов Т гармоники располагаются ближе друг к другу по частоте (линейный спектр становится все более плотным), а амплитуды спектральных составляющих становятся все меньше. При этом вид вычисляемого интеграла (2.21) не меняется. В предельном случае, когда Т —? оо, равные расстояния между спектральными линиями уменьшатся настолько, что спектр станет фактически сплошным, а амплитуды спектральных составляющих окажутся бесконечно малыми. При этом частота следования импульсов coj = 2л/Г—? 0 и превращается в б/со, дискретная переменная /?со, — в мгновенную (текущую) частоту со, а сумма трансформируется в интеграл. Периодическая последовательность импульсов u_n(t) станет одиночным импульсом u (t), и формула (2.27) запишется в виде.

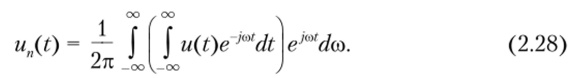
Интеграл в скобках в формуле (2.28) есть комплексная функция частоты. Обозначив его.

получим.

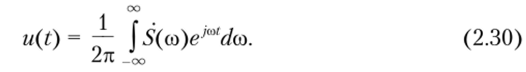
С точки зрения преобразований Фурье физический смысл аргумента функции и (время t или координатах) не играет роли. Однако интуитивно более легко воспринимаются результаты разложения функций времени u (t).

Соотношения (2.29) и (2.30) носят фундаментальный характер в теории сигналов и определяют соответственно прямое и обратное преобразования Фурье (direct, inverse Fourier transform). Они связывают между собой вещественную функцию времени u (t) и комплексную функцию частоты5(со).

Если использовать не угловую частоту со, а циклическую / = со/(2л), то формулы прямого (2.29) и обратного (2.30) преобразования Фурье становятся еще более симметричными, отличаясь лишь знаком в показателе экспоненты:

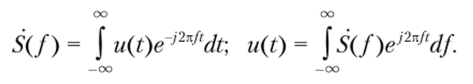
Преобразования (2.29) и (2.30) существуют, если анализируемая функция u (t) удовлетворяет условиям Дирихле (по аналогии с периодическим сигналом), к которым добавляется требование абсолютной интегрируемости сигнала

Итак, прямое преобразование Фурье (2.29) ставит в соответствие сигналу, заданному во времени, его спектральную функцию. При этом осуществляется переход из временной области в частотную. Преобразование Фурье является взаимно-однозначным, поэтому представление сигнала в частотной области (спектральная функция) содержит ровно столько же информации, сколько и исходный сигнал, заданный во временной области. Спектральная плотность — комплексная функция частоты, одновременно несущая информацию как об амплитуде, так и о фазе гармоник.

Поскольку интеграл Фурье (2.29) содержит непрерывную последовательность спектральных составляющих сигнала с бесконечно малыми амплитудами, то функцию 5(со) называют спектральной функцией (спектральной плотностью или просто спектром). Она характеризует интенсивность сплошного распределения амплитуд гармоник непериодического сигнала вдоль оси частот. В этом основное отличие спектральной плотности непериодического сигнала от дискретного спектра периодического сигнала, в котором каждая гармоническая составляющая имеет определенное значение частоты и отстоит от соседней на со, = 2п/Т.

Дискретный спектр периодического сигнала и спектральная плотность непериодического сигнала имеют разные размерности. Размерность амплитудного спектра периодического сигнала совпадает с размерностью самого сигнала — [В| или | А|, а размерность спектральной плотности амплитуд определяется отношением размерности сигнала к размерности частоты — [В/Гц] или [А/Гц].

Поскольку анализируемый непериодический сигнал u (t) и его спектральная плотность ^(со) взаимно-однозначно связаны прямым и обратным преобразованиями Фурье, то последние позволяют аналитически отыскать спектральную плотность, но заданной форме сигнала, и наоборот, его форму по полученной спектральной плотности. В общем случае ^(со) является комплексной величиной. Как комплексная величина она записывается в виде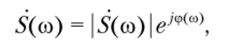

где |5(со)|, cp (co) — соответственно модуль и аргумент комплексной величины, т. е. амплитудный и фазовый спектры сигнала.

Прямое преобразование Фурье четного сигнала u (t) всегда дает вещественную функцию частоты со, а нечетного сигнала u (t) — мнимую функцию частоты.

Нетрудно показать, что интеграл.

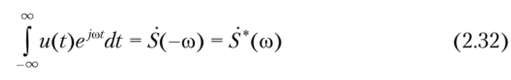
представляет собой комплексно-сопряженную спектральную плотность непериодического сигнала.

Симметрия преобразований Фурье (взаимозаменяемость частоты и времени). Преобразования Фурье вещественных сигналов в комплексной области несимметричны по j. При переходе от прямого преобразования Фурье к обратному необходимо изменение знака при j. Вместе с тем в преобразованиях имеется и существенная симметрия. Пусть четному сигналу u (t) соответствует вещественный спектр 5(со), который, в свою очередь, будет являться четной функцией частоты со, тогда четному сигналу S (t) должен соответствовать спектр Н (со) = 2тш (со). Именно «взаимозаменяемость» аргументов t и со, входящих в ядро ортонормированного базиса ехр (±у'соО> и подразумевают, говоря о симметрии (дуальности) пары интегральных преобразований Фурье (2.29) и (2.30). Симметрия очевидна, если рассматривать комплексные сигналы. Данное свойство удобно использовать в тех случаях, когда по известной паре преобразований Фурье можно найти временную функцию, спектр которой соответствует временной функции известного сигнала, и наоборот.

|Пр|/1мер 2.2Щ. ?' .- - V .'_Л.? ',.3 ' ' *1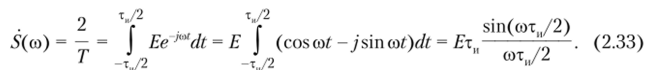

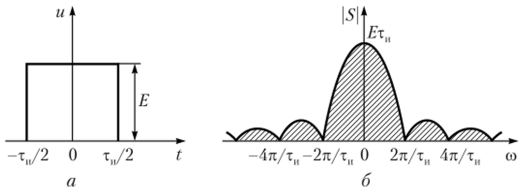
Сравнив выражения для спектральной плотности одиночного прямоугольного импульса (2.33) и спектра их периодической последовательности (2.22), находим, что модуль спектральной плотности и огибающая гармоник дискретного спектра совпадают, но форме и отличаются масштабом по оси амплитуд.

В табл. 2.1 приведены графики ряда импульсов и их амплитудных спектров в области положительных частот, из которых очевидно, что почти все реально применяемые в теории связи импульсы ограниченной длительности теоретически имеют бесконечный амплитудный спектр. Уже упоминаемый принцип неопределенности Гейзенберга применительно к одномерным сигналам можно трактовать так: чем сильнее сигнал u (t) локализован во времени (т.е. чем компактнее «колокол», накрывающий его), тем шире его спектр 5(со) «размазан» в пространстве частот со. И наоборот — чем меньше ширина спектра 5(со), тем больший интервал времени занимает анализируемый сигнал u (t). В общем случае в рамках теории сигналов принцип.

Таблица 2.1

Спектры некоторых распространенных импульсов

Сигнал u (t)		Спектральная плотность. S-S	Амплитудный спектр

неопределенности Гейзенберга означает, что невозможно одновременно с заданной степенью точности зафиксировать частоту сигнала и время его возникновения. И тот и другой параметры фиксируются с некоторой ошибкой, т. е. истинное значение параметров сигнала находится внутри некоторого «окна». Если считать это окно прямоугольным, то его площадь будет равна произведению частоты и времени, и она величина постоянная. Поэтому улучшение разрешения по частоте сопровождается ухудшением разрешения по времени, и наоборот.

У относительно гладких функций спектр быстро убывает (с ростом номера коэффициенты стремятся к нулю). У «изрезанных» функций спектр убывает медленно, поскольку для представления разрывов и изломов функции нужны гармоники с большими частотами. Шириной спектра считают эффективную область частот в пределах которой сконцентрировано 90—95% энергии сигнала. Для колокольного и экспоненциального импульсов, имеющих теоретически бесконечную длительность, для удобства расчетов также вводят понятие эффективной длительности сигнала Т_э, подразумевая иод этим интервал времени, в пределах которого сосредоточена основная доля его энергии.