Капельная модель ядра. 
Формула Вайцзеккера

Описание свойств атомного ядра на основе законов взаимодействия между нуклонами является центральной проблемой теоретической ядерной физики. Однако представления о структуре ядер значительно беднее, чем представления об атомной и молекулярной структуре. Последние понятны настолько глубоко и полно, что дают возможность рассчитывать практически любую характеристику объекта, построенного из ядер и электронов. В то же время, хотя сегодня знания об атомном ядре нельзя назвать ничтожными, они вес же еще недостаточны для построения законченной картины.

В первую очередь, это связано с тем, что количественная теория сильного взаимодействия до сих пор нс создана, и вид ядерных сил приходится подбирать путем подгонки к экспериментальным данным. В атомной физике «богатые» атомные спектры дают возможность это сделать до конца, и если бы о виде электромагнитного взаимодействия ничего нс было известно, его можно было бы установить из спектров. Однако существует лишь одна связанная система из двух нуклонов — дейтрон, имеющий единственный энергетический уровень. Этого, разумеется, недостаточно для построения теории ядра.

Дополнить информацию можно путем экспериментов по рассеянию нуклонов друг на друге. Но даже по всей совокупности экспериментальных данных точный вид взаимодействия может быть установлен лишь тогда, когда силы, действующие между частицами, не зависят от их скоростей, т. е. являются потенциальными. Для нуклонов это нс так.^[1]

Наконец, взаимодействие между двумя нуклонами изменяется, когда они находятся в поле других нуклонов. О роли тройных и вообще множественных сил в ядре мало что известно. Современная теория предсказывает их существование, но не дает возможность рассчитать интенсивность.

Эти и другие трудности можно обойти, используя модельные представления. В моделях ядра заранее задаются или угадываются некоторые его свойства. При этом часто используются аналогии с другими физическими объектами, на первый взгляд, не имеющими ничего общего с ядром. Так, свойство насыщения ядерных сил, следующее из их короткодсйствия, притяжения на больших и отталкивания на малых расстояниях, делает ядро похожим на каплю жидкости. Силы, связывающие молекулы жидкости, тоже насыщаются, а энергия испарения капли линейно увеличивается с увеличением се массы. На этом основании был создан способ описания свойств ядра в модели жидкой капли (К. Вайцзеккер, 1935 г.).

В рамках капельной модели Вайцзеккера получается полуэмпиричсская формула для энергии связи ядра как функции его протонно-нейтронного состава. В эту формулу входят следующие слагаемые.

1) Объемная энергия. Энергия связи ядра тем больше, чем больше в нем нуклонов, или, другими словами, объем ядра V, так как V = (4/3)л7с ~ А. Поэтому в первом приближении энергия связи ядра равна

где а > 0 — константа. Если этим ограничиться, то мы имеем дело с бесконечной ядерной материей (поверхностные эффекты несущественны), лишенной заряда (пренебрегаем кулоновским отталкиванием протонов).

2) Поверхностная энергия. Нуклоны на поверхности ядра связаны менее сильно, чем внутри, так как взаимодействуют с меньшим числом своих соседей. Если в бесконечной ядерной материи провести сферическую поверхность, ограничивающую ядро, и отбросить нуклоны вне ее, то оставшиеся у поверхности нуклоны ядра потеряют примерно половину своих связей. Число потерянных связей пропорционально площади поверхности, равной S = 4лЯ² ~ А¹³. Тогда в (2.19) следует добавить слагаемое, пропорциональное А²'³, со знаком «минус».

где у? > 0 — константа. На поверхностный нуклон действует результирующая сила, направленная внутрь ядра. Поэтому поверхностные нуклоны стремятся сжать ядро, создавая, как в капле жидкости, поверхностное натяжение.

3) Кулоновская энергия. Эту энергию можно оценить, если рассматривать заряд, однородно распределенный, но объему сферы. Тогда энергия отталкивания протонов, уменьшающая W, дается классической электростатической формулой.

(знак примерного равенства соответствует Z"l). В итоге.

4) Энергия симметрии. Ограничиваясь выражением (2.22), нельзя получить правильный ход линии стабильности. Энергия связи является мерой устойчивости ядра, а, согласно (2.22), максимум W достигается при Z = 0, т. е. самые стабильные ядра должны состоять из одних лишь нейтронов. Чтобы получить правильный результат, необходимо учесть, что в легких стабильных ядрах Z = N, и ввести в формулу для энергии связи слагаемое, уменьшающее W при нарушении протонно-нейтронной симметрии. Хорошее согласие с экспериментом достигается, если положить.

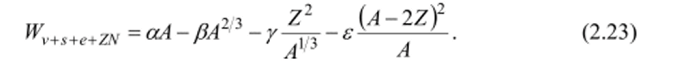
• 5) Энергия спаривания. С помощью формулы (2.23) можно описать энергию связи ядер (за исключением самых легких, с А < 20) с точностью до 1%. Однако в экспериментальных результатах имеются «пульсации» на уровне 1−2 МэВ. Так, энергия отделения нейтрона для некоторых изотопов периодически возрастает, когда число N становится четным, и уменьшается при нечетных N. Следовательно, каждый из нуклонов ядра наиболее сильно связан с остальными, если объединен в пару с другим таким же, а оставшийся одиночный нуклон связан слабее. С точки зрения эффекта спаривания все ядра разбиваются на три группы.
• — Четно-четные ядра (с четными Z и N). Все нуклоны спарены, добавка к W положительна.
• — Нечетно-нечетные ядра (с нечетными Z и N). Не спарено по одному нуклону каждого типа, добавка к Wотрицательна.
• — Ядра с нечетным А. Один из нуклонов не спарен, добавка к W равна нулю (условленная точка отсчета).

Четно-четные ядра являются наиболее устойчивыми, а нечетно-нечетные, напротив, самыми неустойчивыми: стабильных ядер в этой группе всего четыре: ²Н, ⁶Li, ^|0В, ⁱ⁴N. Приведем распределение числа стабильных и долгоживущих ядер в зависимости от значений Z и М (табл. 2.2).

С учетом спаривания нуклонов одного типа наилучшее воспроизведение экспериментальных величин энергии связи даст следующая формула:

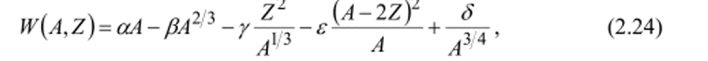
где а = 15,75 МэВ; Р= 17,8 МэВ; у = 0,71 МэВ; е = 23,7 МэВ; д = 0 для ядер с нечетным А; 34 МэВ для четно-четных и -34 МэВ для нечетно-нечетных ядер.

Распространенность ядер в зависимости от значений Z и N

Формула (2.24) носит название формулы Вайцзеккера. Отметим, что четвертое и пятое слагаемые в (2.24) уже не связаны с представлением о ядре как о капле несжимаемой заряженной жидкости. Их появление — результат эмпирически установленных закономерностей, находящих свое объяснение в другой модели — модели ядерных оболочек (см. Лекцию 3).

Формула Вайцзеккера дает правильное представление об энергии связи: для А > 40 расхождение с результатами измерений W не превышает 0,1%. Таким образом, модель позволяет предсказать энергетические условия радиоактивного распада того или другого вида. В частности, с ее помощью можно достаточно точно определить положение линии стабильности на протоннонейтронной диаграмме. Для этого достаточно, зафиксировав массовое число А, найти изобар с наибольшей энергией связи. Дифференцируя (2.24) по Z и приравнивая к нулю производную, после подстановки параметров получаем, что.

Условие (2.25) определяет в рамках модели Вайцзеккера соотношение между числом протонов и нейтронов для ядер, устойчивых относительно рраспада (дорожка стабильности). Ядра, содержащие избыток протонов, нестабильны относительно р⁺-распада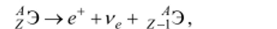

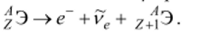
а ядра с избытком нейтронов — относительно р-распада¹

Подробнее об этом см. Лекцию 8.

• [1] Это свойство ядерных сил будет обсуждаться в Лекции 3.