Оптимизация затрат в условиях неопределенности и риска

На практике выбор оптимальной стратегии в процессе планирования затрат можно осуществить с помощью теории игр. Теория игр рассматривает задачи выбора оптимального поведения с учетом возможных действий других участников и случайных событий. Простейшей игровой ситуацией является такая, когда имеются два участника, преследующие противоположные интересы. Такая игра называется антагонистической. В антагонистических играх неопределенность для каждого игрока состоит в том, что заранее не известно, какую стратегию выберет в каждой партии его противник.

Принятие решений в условиях неопределенности носит название «игр с природой» и изучается теорией статистических решений. Под «природой» понимаются не только природно-климатические явления, но и комплекс неопределенностей, связанных с состоянием техники, настроением и здоровьем людей, т. е. не зависящих от лица, принимающего решения. Различные комбинации условий, которые могут встретиться при выполнении планируемого мероприятия, называются состояниями природы. Неопределенность ситуации заключается в том, что не известно, в каком из возможных состояний будет находиться «природа» в момент реализации управленческого решения.

Рассмотрим решение задачи выбора оптимальной стратегии на примере. Строительная организация заключила с заводом железобетонных изделий договор на ежедневную поставку раствора марки Ml50 на сумму 30 тыс. р. Если в течение дня раствор не поступает, организация несет убытки в размере 100 тыс. р. из-за простоя рабочих. Строительная организация может послать поставщику свой транспорт (дополнительные расходы — 4 тыс. р.), однако опыт показывает, что в 40 случаях из 100 транспорт возвращается ни с чем. Можно увеличить вероятность получения раствора до 80%, если предварительно послать на завод своего представителя, однако это потребует дополнительных расходов в 4 тыс. р.

Можно заказать дневную норму раствора у другого, надежного поставщика по более высокой цене (до 50%). Однако, кроме расходов на транспорт (4 тыс. р.), возможны дополнительные затраты в размере 8 тыс. р., связанные со сверхурочной работой бригад, реализующих лишний раствор, если в тот же день будет поставка завода ЖБИ. Какой стратегии следует придерживаться строительной организации, если заранее не известно, поступит или не поступит раствор завода ЖБИ?

Прежде всего перечислим возможные стратегии поставщика. Их две: И, — поставка своевременная, П₂ — поставки нет. У строительной организации, согласно условию задачи, четыре стратегии: С, — не принимать никаких дополнительных мер; С₂ — послать к поставщику свой транспорт; С, — послать к поставщику своего представителя и транспорт; С₄ — заказать дополнительно раствор на другом заводе.

Возможны восемь ситуаций, описывающих все комбинации из четырех стратегий строительной организации и двух стратегий завода-поставщика (табл. 4.1).

Если в общем случае у первого игрока т возможных стратегий, а у второго — п, то всегда образуется т х п возможных ситуаций, каждой из которых соответствует определенный платеж одного игрока другому.

При большом количестве ситуаций удобнее использовать платежную матрицу. Для этого составляется прямоугольная матрица, имеющая т строк (по числу стратегий первого игрока) и п столбцов (по числу стратегий второго игрока).

На пересечении /-й строки и /-го столбца ставится платеж второго игрока первому в ситуации, когда применены то-я стратегия первым игроком и п-я стратегия — вторым.

Таблица 4.1

Затраты и ущерб по вариантам ситуаций

Если в данной ситуации выигрывает второй игрок, платеж будет иметь знак «минус». Расчетная матрица нашей игры размерностью 4×2 представлена в табл. 4.2. Все платежи имеют знак «минус», так как обозначают в нашем примере затраты строительной организации.

Задача руководства — определить оптимальную стратегию, обеспечивающую минимум ожидаемых убытков в условиях неопределенности относительно поведения поставщика.

Выбор стратегии в условиях, описанных в табл. 4.2, зависит от надежности поставщика, выраженной количественно в терминах вероятности. Пусть, например, она равна 40% (это означает, что своевременная поставка имеет место с вероятностью 0,4). Рассчитаем ожидаемые убытки (отрицательный выигрыш) при применении четырех стратегий:

Оптимальной будет стратегия С₃, при которой организация несет минимальные расходы (-46,4 тыс. р.).

Расчетная матрица

Таблица 4.2

Дадим геометрическую интерпретацию рассмотренной игры (рис. 4.3). Отложим по горизонтальной оси надежность поставщика, измеряемую вероятностями в диапазоне от 0 до 1, и обозначим ее У,; У₂ = 1 — У, - ненадежность поставщика. Числа У, и Y₂, равные в сумме единице, показывают, с какой вероятностью поставщики применяют чистые стратегии П, и П₂ в каждой партии. Совокупность стратегий П, и П₂ с вероятностями осуществления У, и У₂ называется смешанной стратегией. Точки У, = 0 и У₂ = 1 на рис. 6.3 соответствуют второй и первой чистым стратегиям поставщика, а все точки 0 < У, < 1 внутри отрезка — смешанным стратегиям.

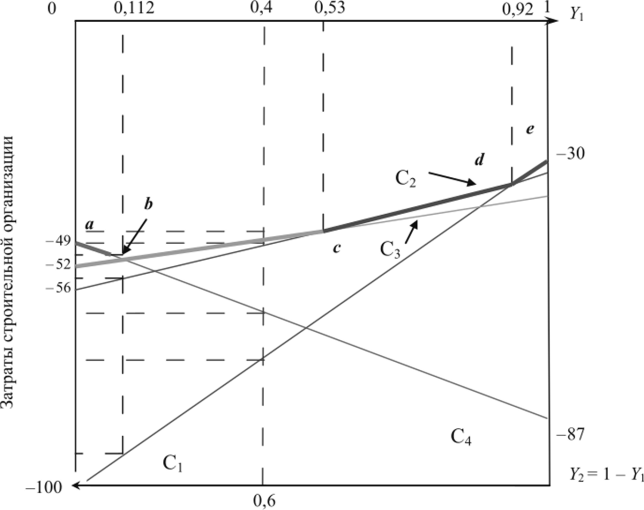
Рис. 4.3. Смешанные стратегии.

Смешанных стратегий у любого игрока бесчисленное множество. Построим графики ожидаемых затрат при применении своих чистых стратегий против смешанных стратегий поставщика. Построение начнем с четвертой стратегии. Если поставщик абсолютно надежен (т. е. всегда применяет стратегию П, и, значит, У, - 1, У, = 0), затраты строительной организации в соответствии с платежной матрицей равны -87 тыс. р. Отложим на графике точку с координатами (1; -87). Если поставщик абсолютно ненадежен, т. е. всегда применяет стратегию У₂ (У, = 0, У₂ = 1), тогда затраты строительной организации равны -49 тыс. р. и нужно отложить точку с координатами (0; -49).

Если надежность поставщика 0 < У, < 1, тогда ежедневные затраты строительной организации, применяющей четвертую стратегию против смешанной стратегии поставщика, зависят от вероятности У:

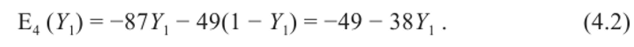
Эта функция изображается прямой линией С₄. Аналогично строятся графики функций ожидаемых затрат при применении каждой чистой стратегии против смешанной стратегии поставщика:

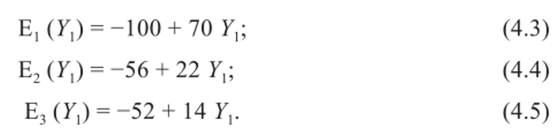
При надежности поставщика У, = 0,4 до пересечения с линиями функций ожидаемых затрат обнаружим, что оптимальной будет стратегия С₃, обеспечивающая минимальные затраты — 46,4 тыс. р. Из рис. 6.3 видно, что, если надежность поставщика У, > 0,112, выгоднее всего применять четвертую стратегию; при надежности поставщика 0,112 < FY_X У, > 0,921 — вторая и, наконец, при 0,921 < У, < 1 — первая.

Эти критические значения надежности получены из совместного решения уравнений (4.2)-(4.5), взятых попарно: (4.4) и (4.4) — точка b, (4.3) и (4.4) — точка с, (4.2) и (4.3) — точка d. Ломаная линия abede показывает, как изменяются затраты при изменении надежности поставщика от 0 до 1. Как видно из графика, увеличение надежности поставщика не приводит автоматически к уменьшению расходов строительной организации. Когда надежность поставщика растет от 0 до 0,112, затраты строительной организации возрастают от 49 р. до Н₄ (0,112) = -49 — 38×0,112 = -53,3 тыс. р. Увеличение затрат вызвано тем, что раствор закупается у другого поставщика, а нерегулярные поставки основного поставщика (с вероятностью У, = 0,112) приводят к дополнительным затратам.

При надежности поставщика У, = 0,112 затраты строительной организации максимальны (из всех возможных) при разумном выборе своих стратегий. (Этот максимум зависит от величины затрат, условно выбранных в начале задачи.).

Если бы игра была антагонистической, т. е. поставщик стремился нанести строительной организации максимальный ущерб, его оптимальная надежность равнялась бы У, = 0,112. При этом затраты строительной организации составили бы -53,3 тыс. р. и оптимальными были бы стратегии С₃ и С₄ (точка Ь находится на пересечении линий С₃ и С₄).

Для выбора смешанной стратегии строительной организации рассмотрим квадратную подматрицу исходной платежной матрицы, получающуюся после исключения первой и второй стратегий (табл. 4.3).

Расчетная матрица

Таблица 4.3

Эти стратегии исключаются, потому что в антагонистической игре поставщик будет обеспечивать нерегулярные поставки раствора с надежностью 0,112, а против такой его смешанной стратегии первая и вторая стратегии строительной организации неэффективны. При их применении расходы резко возрастают (до 90,55 и 54,03 тыс. р. соответственно).

Построим графики затрат строительной организации, применяющей смешанную стратегию, состоящую из чистых стратегий С₃ и С₄, против каждой чистой стратегии поставщика (рис. 4.4).

Обозначим через Х_} вероятность применения стратегии С₃, а через Х₄ — вероятность применения стратегии С₄. Заметим, что при Х_} = 0 Х₄ = 1; при Х_} = 1 Х₄=0иХ₃+Х₄ = 1.

Из графика (см. рис. 4.4) видно, что оптимальная смешанная стратегия строительной организации включает стратегии С₃ и С₄, применяемые с вероятностью Х_} = 0,685 и Х₄ = 0,315. Оптимальными будут затраты строительной организации (называемые в случае антагонистической игры ценой игры) в точке g. Из рис. 4.4 видно, что в антагонистической игре строительной организации не следует отступать от своей оптимальной смешанной стратегии X, = Х₂ = Х₃ = 0,685; Х₄ = 0,315, поскольку затраты возрастут (в направлении утолщенных линий). При Х_ъ < 0,685 поставщик станет применять чистую стратегию П" при Х₃ > 0,685 — чистую стратегию П₂.

Итак, при антагонистической игре (когда каждый из игроков стремится нанести противнику максимальный ущерб) оптимальная стратегия строительной организации будет следующей: X, =Х₂ = 0, Х_} = 0,685, Х₄ = 0,315; завода железобетонных изделий: К, = 0,112, У₂ = 0,888. При этом цена игры (ожидаемые оптимальные затраты строительной организации) равна 53,3 тыс. р.

Рис. 4.4. Чистые стратегии поставщика.

Игры против природы. Так как наша игра неантагонистическая, такое ее решение принципиально неверно, ибо лишает строительную организацию возможности снизить затраты по сравнению с оптимальными. Действительно, поставщик не стремится нанести строительной организации максимальный ущерб, поэтому его надежность может быть любой, совсем необязательно наихудшей с точки зрения строительной организации (как мы видели выше, наихудшая надежность поставщика равна 0,112).

Если, например, надежность поставщика равна 0,4, а строительная организация продолжает применять оптимальную для антагонистической игры смешанную стратегию, то ее ожидаемые затраты не снижаются. Действительно,.

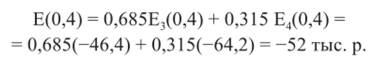
Чтобы снизить затраты при данной надежности поставщика, необходимо отказаться от оптимальной смешанной стратегии и, как мы обнаружили в предыдущем расчете, применять чистую третью стратегию. Затраты при этом снизятся до 46,4 тыс. р.

Таким образом, особенностью решения игр против природы в условиях определенности является то, что смешанная стратегия природы задана, т. е. известны все вероятности состояний Y_pj =1,2, …, п nY_f = 1. Это позволяет для каждой г-й чистой стратегии активного игрока рассчитать математическое ожидание его выигрыша против известной смешанной стратегии природы по формуле.

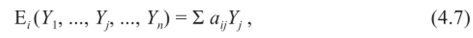
где a_tj — элемент платежной матрицы, расположенный на пересечении г'-й строки и /-го столбца.

Максимальный элемент в рассчитанном столбце математических ожиданий выигрышей J = max Е, (У,Y,…, У") определяет наивыгоднейшую стратегию активного игрока и численно равен максимально возможному выигрышу. Если максимальных элементов в этом столбце два и более, могут применяться соответствующие им стратегии как в чистом виде, так и в любом сочетании. Такой подход для решения игр против природы возможен, когда вероятности тех или иных состояний природы заданы. Чаще всего информация о таких вероятностях отсутствует. При этом для выбора оптимальной стратегии в качестве критерия можно применить максимум математического ожидания выигрыша (критерий Лапласа), но этот критерий может использоваться только для равномерного распределения вероятностей У, = /п (табл. 4.4).

Таблица 4.4

Расчетная матрица

Рассмотрим другие критерии, применяемые при решении игр природы в условиях неопределенности:

1. Максиминный критерий Вальда. Выбирается решение, гарантирующее получение выигрыша не меньше, чем максимин:

В нашей игре при любом поведении поставщика строительная организация может выбрать любую из своих чистых стратегий. При каждой стратегии могут быть два исхода. Для гарантии надо учесть тот, который дает наименьший выигрыш. Запишем его в столбец минимумов строк (табл. 4.5). Из этих строк можно выбрать такую, при которой этот минимальный выигрыш будет максимальным. Это и есть оптимальная стратегия, выбранная в соответствии с вышеприведенной формулой. В табл. 4.5 определена также минимаксная стратегия поставщика, для чего из каждого столбца выбирается максимальный выигрыш и принимается стратегия, дающая строительной организации минимальный из этих максимальных выигрышей. Этому выигрышу соответствует вторая стратегия поставщика.

Таблица 4.5

Расчетная матрица

Таким образом, максиминная стратегия строительной организации нейтрализует минимаксную стратегию поставщика. Очевидно, такой подход может быть продиктован только крайним пессимизмом в оценке обстановки.

2. Максимаксный критерий предполагает, что обстановка будет для нас наиболее благоприятной, поэтому мы должны выбрать решение, обеспечивающее максимальный выигрыш из максимально возможных:

Используя максимальный критерий в задаче, получаем J_m = -30 тыс. р., т. е. строительная организация не должна ничего предпринимать (решение С" табл. 4.6). Это критерий абсолютного оптимизма, так как он не учитывает, что состояние природы не всегда будет наиболее благоприятным.

3. Критерий пессимизма — оптимизма Гурвица представляется логичным при выборе решения вместо двух крайностей в оценке ситуации (оптимизм — пессимизм) придерживаться некоторой промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего поведения природы. Такой компромиссный критерий был предложен Гурвицсм. Согласно ему, необходимо для каждого решения определить линейную комбинацию минимального и максимального выигрышей и принять стратегию, для которой эта величина окажется наибольшей:

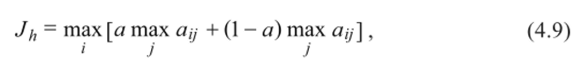
где а (0 > а < 1) — степень оптимизма.

При а = 0 критерий Гурвица переходит в максиминный критерий Вальда; при а = 1 он совпадает с максимаксным критерием. На выбор значения степени оптимизма влияет мера ответственности: чем серьезнее последствия ошибочных решений, тем больше желание застраховаться, тем ближе а к нулю. Влияние степени оптимизма на выбор решения в рассматриваемой задаче показано в табл. 4.6.

Таблица 4.6

Влияние степени оптимизма на выбор решения

Величина J_m для каждого значения а отмечена значком * (см. табл. 4.5). При а = 5/9 критерий Гурвица рекомендует в задаче решение С₃; при 5/9 8/9 — решение С₂; в остальных случаях — С,.

4. Критерий Сэвиджа (критерий минимакса риска). Суть данного критерия состоит в выборе решения, не допускающего чрезмерно высоких потерь. Для этого строится так называемая матрица рисков, которая показывает, каким будет убыток, если выбрать не лучшее решение.

Риском игрока при выборе некоторого решения А₄ в условиях П₍ называется разность между максимальным выигрышем, который можно получить в этих условиях, и выигрышем, который получит игрок в тех же условиях, применяя стратегию А. Обозначим эту величину r_ir Если бы игрок знал заранее будущее состояние природы П, он выбрал бы стратегию, которой соответствует максимальный элемент в данном столбце: шах a_(j.

Тогда, по определению, риск.

Матрица рисков строится так:

• • для каждого состояния природы (столбца) определяется наибольший элемент;
• • элемент матрицы рисков получается вычитанием соответствующего элемента платежной матрицы из максимального элемента данного столбца.

Критерий Сэвиджа рекомендует в условиях неопределенности выбирать решение, обеспечивающее минимальное значение максимального риска:

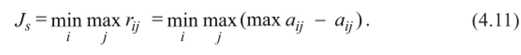
В правом столбце матрицы (табл. 4.7) приведены максимальные риски для каждого решения.

Матрица рисков

Таблица 4.7.

5. Критерий Байеса — Лапласа. Применяя этот критерий, отступают от условий полной неопределенности, считая, что возможным состояниям природы можно приписать определенную вероятность их наступления и, определив математическое ожидание выигрыша для каждого решения, выбрать то, которое обеспечивает наибольшее значение выигрыша:

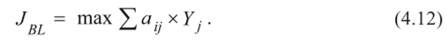
Принцип Байеса — Лапласа можно применять, если изучаемые состояния природы и принимаемые решения многократно повторяются. Тогда, например, основываясь на частотах появления отдельных состояний природы в прошлом, можно оценить вероятности их появления в будущем статистическими методами. При единичных, не повторяющихся решениях принцип Байеса — Лапласа применять нельзя, даже если состояния природы повторяются. Это вызвано тем, что такие решения нарушают стационарность распределения вероятностей состояний природы.

Предположим, что строительная организация, прежде чем принять решение, проанализировала, насколько точно поставщик ранее выполнял сроки поставок, и выяснила, что в 25 случаях из 100 материал поступал с опозданием. Отсюда следует, что состоянию П, можно приписать вероятность У, = 0,75, а состоянию П₂ — вероятность У₂ = 0,25. Тогда, согласно критерию Байеса — Лапласа, оптимальным является решение С₂ (табл. 4.8).

Результаты расчетов (табл. 4.9) показывают, что оптимальное поведение во многом зависит от принятого критерия оптимизации.

Выбор критерия влечет за собой принятие решения, которое может отличаться от принятого в соответствии с другим критерием. Однако ситуация никогда не бывает настолько неопределенной, чтобы нельзя было получить хотя бы частичную информацию относительно вероятностей распределения состояний природы. Оценив распределение вероятностей состояния природы, применяют критерий Байеса — Лапласа либо проводят эксперимент, позволяющий уточнить поведение природы.

Таблица 4.8

Расчетная матрица

Результаты расчетов

Таблица 4.9