Натуральное число — мощность конечного множества

Вопросы для обсуждения.

• 1. В чем суть теоретико-множественного подхода к формированию основных понятий курса математики начальной школы?
• 2. Что такое натуральное число с теоретико-множественной точки зрения? Что обозначают знаки: «три», 3?
• 3. Как в рамках теоретико-множественной концепции раскрыть для младших школьников отношение сравнения чисел?
• 4. Как связаны и чем различаются понятия «объединение множеств» и «сложение натуральных чисел»?
• 5. Какие подходы к раскрытию смысла вычитания возможны в теоретикомножественной трактовке натурального числа?
• 6. В чем отличие отношений «больше» и «больше на…» на множестве натуральных чисел?
• 7. Какие определения умножения возможны для чисел — мощностей конечных множеств?
• 8. В чем достоинства определения умножения, данного Н. И. Лобачевским?
• 9. Какие аналогии между вычитанием и делением могут способствовать усвоению детьми смысла этих действий?
• 10. Каковы возможности теоретико-множественного подхода для реализации принципа наглядности при обучении арифметике натуральных чисел?

Другой важнейшей теоретической моделью арифметики является модель, основой которой служит теоретико-множественный подход, моделирующий натуральное число как мощность конечного множества. В практике начального обучения математике именно эта модель, как правило, является основной.

Г. Кантором (1845—1918) создана теория множеств, оказавшая большое влияние как на развитие, так и на обучение математике. Важнейшим понятием этой теории является понятие равномощности множеств, позволившее создать теорию количественного числа.

Два множества являются равномощными, если между элементами этих множеств можно установить взаимно однозначное соответствие, при котором у каждого элемента одного множества имеется единственный образ в другом, и обратно, у каждого элемента второго множества имеется единственный прообраз в первом. Для предметных совокупностей, рассматриваемых в начальной школе, такое соответствие означает, что каждому предмету одной совокупности ставится в соответствие единственный предмет другой и при этом не остается предметов, не входящих в какую-нибудь пару, где один элемент пары из одного множества, а другой — из другого.

Отношение равномощности множеств есть отношение эквивалентности, оно рефлексивно (каждое множество равномощно самому себе); симметрично (если множество А равномощно й, то и множество В равномощно А); транзитивно (если множество А равномощно й, а множество В равномощно С, то, А равномощно С). Это значит, что по отношению равномощности все множества разбиваются на классы равномощных между собой множеств. То общее свойство, которое присуще всем множествам одного и того же класса, называют мощностью или численностью каждого из множеств данного класса.

На рис. 3.4 показано, что сущность натурального числа как мощности конечного множества можно изобразить наглядно, где представлены несколько множеств, входящих в один и тот же класс эквивалентности и, следовательно, каждое из них является представителем данного класса эквивалентности, т. е. обозначает некоторое конкретное натуральное число а.

Рис. 3.4. Наглядное изображение натурального числа как мощности конечного множества Сравнение мощностей представителей каждого класса эквивалентности приводит к построению неограниченно продолжаемой последовательности, каждому элементу которой присваивается собственное имя, обозначающее то общее, что есть у каждого множества данного класса (рис. 3.5). Нетрудно заметить, что каждой конечной мощности, кроме 0, можно поставить в соответствие единственную цифру в смысле Гильберта.

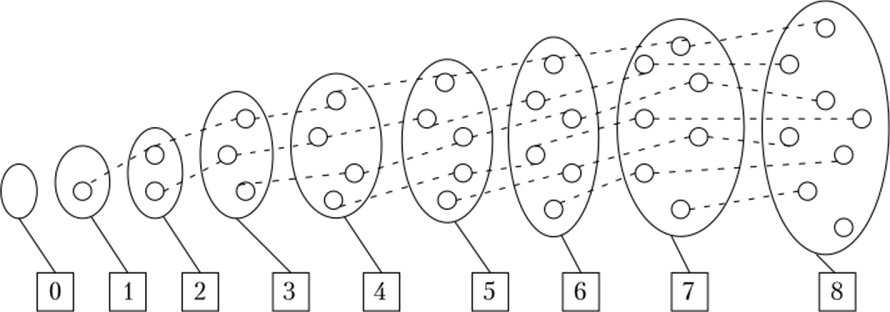
Рис. 35. Сравнение мощностей представителей каждого класса эквивалентности Тем самым открывается возможность количественной оценки любой предметной совокупности методом пересчета, суть которого показана на рис. 3.6.

Рис. 3.6. Иллюстрация метода пересчета.

Нетрудно видеть, что при пересчете предметной совокупности производятся два действия:

• 1) устанавливается взаимно однозначное соответствие между отрезком натуральных чисел и пересчитываемыми предметами;
• 2) пересчитываемая совокупность упорядочивается, каждому ее элементу приписывается определенный номер.

Возникает вопрос: не зависит ли результат счета от способа упорядочения? Покажем, что это не так. Пусть при одном способе пересчета каждый элемент совокупности получил номера ц, г₂,…, ц, а при другом — j_x, j₂,… J", и допустим, что k*n. Поставив каждому элементу одного упорядочения его самого, но в другом упорядочении мы установим взаимно однозначное соответствие, что противоречит неравенству k ^ п. Следовательно, последний из используемых при пересчете знаков обозначает численность пересчитываемой совокупности.

Для мощностей конечных множеств естественным образом определяются арифметические операции.

Сложение. Пусть а — мощность множества А, b — мощность множества В, А и В не имеют общих элементов, тогда сумма а + b — это мощность объединения множеств Л и В:

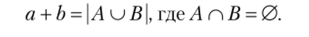
Согласно этому определению может быть найдена сумма любых двух конечных мощностей. Например, сумма 3 + 4 наглядно представляется на рис. 3.7, где в квадратиках указаны мощности объединяемых множеств. Такое кодирование сложения графическими знаками-индексами, построенное в точном соответствии с определением сложения, является в то же время необходимым условием формирования визуально-пространственных когнитивных компонент понятийного образа сложения.

Рис. 3.7. Наглядное представление суммы 3 + 4.

При этом устанавливается смысл вычитания как операции, производной от сложения: разность а — b — это такое число, которое нужно прибавить к Ь, чтобы получить а, т. е. верно равенство.

Разность а — b существует тогда и только тогда, когда каждое из уравнений.

имеет одно и то же единственное решение, т. е. х = у = а — Ь. Так как указанные уравнения имеют решения не для любых натуральных а и b, то вычитание на множестве натуральных чисел принято называть частичной операцией на этом множестве.

Такое положение дел означает, что для нахождения, например, разности 15−8 надо найти число, которое в сумме с 8 дает 15. Такое рассуждение является совершенно общим, являясь существенным вкладом в структуру понятийного образа вычитания, его операционально-логической когнитивной составляющей. Кроме того, этим устанавливаются содержательные связи между сложением и вычитанием, раскрывая не только смысл вычитания, но и обогащая содержание понятия «сложение».

Умножение натуральных чисел как мощностей конечных множеств определяется различными способами.

Определение 3.1. Пусть а = А |, b = В. Тогда.

где |Л,| = a, i= 1,2,…, п; п = Ь; Л, п А-_}- 0; b отлично от 0 и 1.

Другими словами, произведение а на b, где а и b — мощности конечных множеств, есть объединение b множеств, каждое из которых имеет мощность а, и эти множества попарно не пересекаются.

Если положить а = 3, b = 4, то произведение а х b согласно данному определению иллюстрируется знаками-индексами (рис. 3.8).

Данное определение умножения дает правило нахождения произведения любых чисел, хотя практически уже для чисел, превышающих десять, это затруднительно. Тем нс менее такая процедура, наглядно представленная для частного случая 3 • 4 на рис. 3.8 адекватно определению, делает «видимым» смысл умножения. Диалектика отношений между общим, частным и единичным (общее проявляется только через единичное, частные случаи подтверждают общее) показывает, что данное обозначение умножения знаками-индексами выполняет прежде всего познавательную функцию.

Определение 3.2. Пусть а = А, b = В. Тогда.

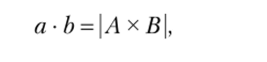
где А х В — декартово произведение множеств А и В.

Другими словами, произведение мощностей конечных множеств есть мощность декартова произведения этих множеств.

Если положить а = 4, b = 3, то согласно данному определению произведение этих чисел находится как мощность декартова произведения Ах В, где А = {Х₁₉ Х₂, Х₃, Х₄}, А = 4, В = {Y_t, Y₂, У₃}, |Я| = 3. Тогда произведение 3 • 4 есть мощность множества элементов, представленного элементами в ячейках таблицы.

Декартово произведение множеств Ах В

Определение 3.3 (по Н. И. Лобачевскому). Произведение а на Ъ производится из а так же, как b из единицы (b отлично от нуля).

Для чисел — мощностей конечных множеств суть умножения согласно этому определению знаками-иконами представляется так, как показано на рис. 3.9, где каждая единица числа 4 «замещается» числом 3.

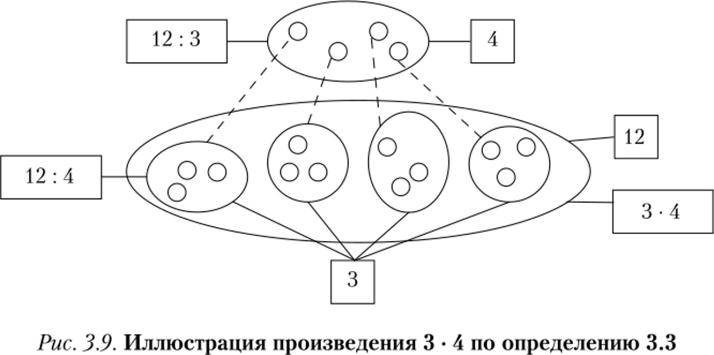
Достоинства этого определения и соответствующего ему кода в том, что здесь явно представлены оба множителя, и, кроме того, наглядно показана различная роль множителей, что увеличивает познавательную ценность как самого определения, так и его визуально-пространственного представления. Каждый элемент множества, мощность которого есть второй множитель, производит множество мощности, равной первому множителю.

Вместе с умножением естественно рассматривается деление. Если каждое из уравнений

при b Ф 0 имеет единственное решение и эти решения совпадают, то.

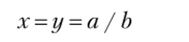
называется частным от деления а на Ь. Другими словами, частное а / b есть такое число, которое при умножении на b дает а, что означает справедливость равенств.

Так как функциональная роль множителей в произведении различна, то различен и содержательный смысл деления в зависимости от того, результатом решения какого из исходных уравнений является частное. Если аЬ — мощности конечных множеств и решение уравнения Ъ • х = а существует, то х показывает, сколько раз по b содержится в а. В этом случае говорят о делении по содержанию. Если же имеет место решение уравнения х • b = а, то х показывает, какова величина каждой из b равных частей в а. В этом случае говорят о делении на равные части.

Разумеется, значение частного не зависит от того, как именно делили, в силу того что решения уравнений b х = а, у b = а, если они существуют, совпадают. Но, решая задачи: «1) 12 конфет разделили между 4 детьми поровну. Сколько конфет получил каждый ребенок?», «2) 12 конфет надо разделить детям так, чтобы каждый получил 4 конфеты. Сколько детей получат конфеты?», легко заметить, что в первой задаче частное 12/4 означает деление на равные части, а во второй — деление по содержанию.

Так как существуют три определения умножения чисел — мощностей конечных множеств, каждое из которых диктует свой способ нахождения произведений, то возникает вопрос: не будут ли различными произведения одних и тех же чисел, найденные в соответствии с каждым определением? Или, что-то же самое, не определены ли различные операции? Таким образом, необходимо доказать равносильность данных определений.

Докажем сначала равносильность определений 3.1 и 3.2.

Пусть а = Л = |{Х, Х₂, Х_а}, Ь = В = |{У, У₂,Y_b}. Тогда согласно определению 3.1 произведение а • b есть мощность объединения.

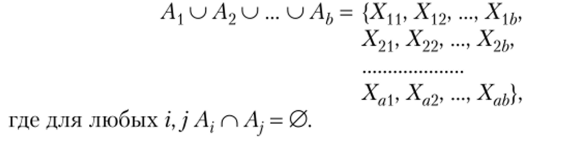
По определению 3.2 произведение ах Ь есть мощность декартова произведения множеств А и В:

(Х_а, г,), (Х_а, У₂)>-> (Х_а, Y_b)}.

Между множествами А, и А₂ и… и А_ь и А х В устанавливается взаимно однозначное соответствие, если каждому Хц е А^ и А₂ и … и А_ь поставить в соответствие пару (Х_;, Y.). Отсюда следует справедливость равенства.

т.е. равносильность определений 3.1 и 3.2.

Докажем равносильность определений 3.1 и 3.3.

По определению 3.3 произведение а х Ь есть мощность множества, которое производится замещением каждого элемента множества В элементами множества А:

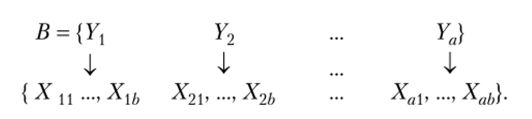
Обозначив элементы произведенного множества Х_{р где i есть номер элемента В, замещением которого является A, aj — номер данного элемента в множестве А, получим, что устанавливается взаимно однозначное соответствие между произведенным множеством и множеством А_х и А₂ и … и А_ь. Это и доказывает равенство их мощностей, а следовательно, эквивалентность определений 3.1 и 3.3. Так как определение 3.1 равносильно определению 3.2, определение 3.1 равносильно определению 3.3, то в силу симметричности и транзитивности отношения равносильности все три определения равносильны.

Рассмотрим сравнение мощностей конечных множеств.

Определение 3.4. Если а = А, b = |5|, то а а) тогда и только тогда, когда найдется С, а В такое, что С Ф В и | А = С.

На рис. 3.10 знаками-индексами закодировано отношение а < Ь, где я = 3, b = 7.