Основные свойства уравнений акустики

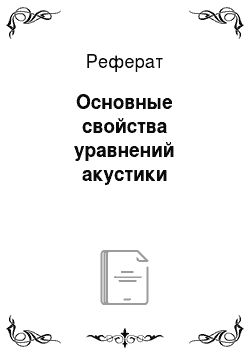
Приведем (6.26) к каноническому виду. Дпя этого умножим второе уравнение на 1/(роСо), а затем сложим с первым уравнением и вычтем из него. Получим.

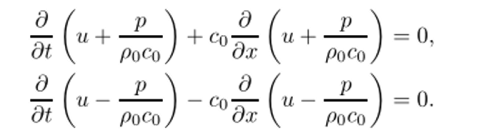
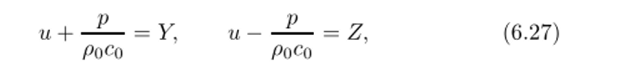
Если ввести обозначения то система запишется в виде.

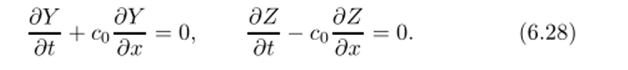
Видим, что система представляется в виде двух независимых уравнений, каждое из которых представляет простейшее гиперболическое уравнение переноса (4.1).

Прямой подстановкой в (6.28) убеждаемся, что произвольные дифференцируемые функции fug аргумента x—cot и х+создают общее решение системы:

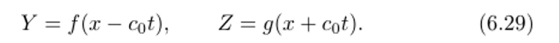
Через эти функции можно выразить искомые неизвестные и и р. Для этого нужно разрешить систему линейных уравнений (6.27). В результате такой операции получим.

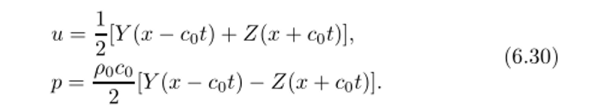
Величины Y и Z, определенные выражениями (6.29), называются инвариантами Римана. Как видно из (6.28), инвариант Y = = и+р/(роСо) остается постоянным вдоль прямой x—cot = const, т. е. график функции Y (х) перемещается с течением времени вправо со скоростью со. Аналогично вдоль прямой x+cot = const сохраняется постоянное значение инварианта Z = и — р/(ро^о) • Здесь со — скорость распространения малых возмущений (скорость звука). Линии x±cot = const являются характеристиками системы (6.28). Для того чтобы выделить единственное решение, соответствующее конкретному физическому процессу, необходимо функции fug выбрать так, чтобы выполнялись поставленные начальные условия, кроме того, необходимо обеспечить выполнение и граничных условий, если задача решается в области конечного размера.

Например, если начальные данные известны лишь на отрезке ЛВ х ^ х ^ а?2, и (х, 0) = и₀(х), р (х, 0) = р₀(х) (рис. 6.1), то решение может быть построено лишь в некоторой ограниченной области. Покажем это. На основании равенств.

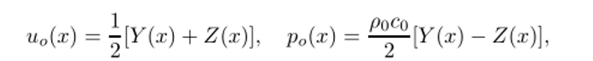
являющихся следствием общего решения (6.30), получим значения инвариантов Y и Z в области задания начальных условий на отрезке АВ:

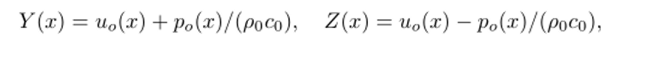
которые могут быть использованы для определения решения по соотношениям (6.30).

Это решение будет иметь место внутри характеристического треугольника AM В. Если расчетная точка Т лежит внутри этого треугольника (см. рис. 6.1), то, перемещаясь по характеристикам линиям сохранения значений инвариантов, мы можем установить из заданных начальных данных в пределах отрезка АВ значения инвариантов Y и Z и таким образом найти параметры в точке Т :

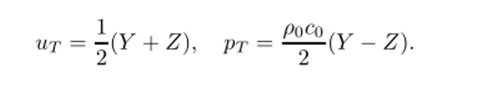
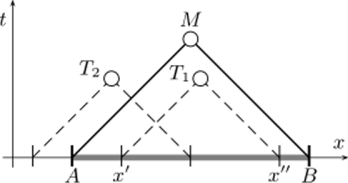
Рис. 6.1. Область зависимости и характеристики уравнений акустики.

Если точка Т-2 лежит за пределами характеристического треугольника, то левая характеристика х — c$t = const пересекает ось Ох за пределами отрезка А В и значение инварианта Y в точке Т2 будет не определено. Таким образом, треугольник AM В представляет собой область зависимости решения от начальных данных, заданных на отрезке АВ .

Рассмотрим важный для расчета случай, когда начальные данные не являются непрерывными, а именно, простейшую задачу Коши с разрывными данными следующего вида:

Эта задача определена в бесконечной области и поэтому нс требует выставления граничных условий, а ее решение определено во всем пространстве. Начальные данные представляют две полубесконечные области с постоянными значениями переменных. Эти области разделяются точкой х*, в которой имеет место разрыв начальных данных. Такая задача в отечественной литературе называется задачей о распаде произвольного разрыва³, а в зарубежных источниках «проблемой Римана».

На рис. 6.2 приводятся начальный разрыв давления, характеристики в плоскости х, t, а также, для наглядности, распределение давлений вдоль оси Ох и динамика его изменения во времени.

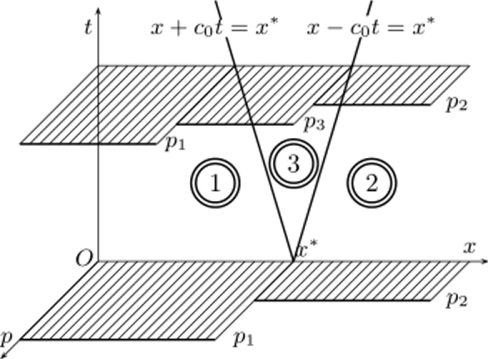
Рис. 6.2. Распад разрыва давления в акустической задаче.

В области 1 параметры постоянны в силу постоянства начальных условий левее точки разрыва х*. Действительно, записывая постоянство инвариантов Римана вдоль характеристик, получим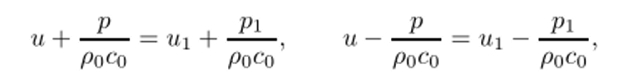

откуда следует, что в области 1 и = щ, р = Р- Аналогично в области 2 сохраняются «правые"невозмущенные величины: и = U2, Р = = р2 при х > х* + cot. В области 3 в любую рассматриваемую точку Т приносятся значения инварианта Y из области 1 и Z из области 2. Следовательно, величины и и р в области 3 могут быть определены из соотношений.

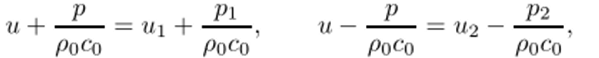
³Можно показать, что решение этой задачи существует при любом произвольном разрыве начапьных данных, что и отражено в ее наименовании.

разрешая которые, получим при х* — c$t < х < х* + c^t

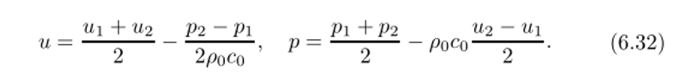
Таким образом, параметры в области 3 также постоянны и их значения даются формулами (6.32). Решение задачи о распаде разрыва имеет разрывы вдоль линий x + cqI = х* и х — cot = х*, т. е. не является непрерывным (не удовлетворяет классическому определению решения дифференциальной задачи). Оно называется обобщенным решением задачи о распаде разрыва (в акустическом приближении). Его можно рассматривать как предел классических «гладких"рсшсний задачи, в которой первоначальный разрыв параметров в точке х* как бы «размазан"на некоторую область.