Аппарат нечетких множеств и описание биообъектов

Низкая; 2 — комфортная; 3 — повышенная; 4 — высокая Лингвистическая переменная — это переменная более высокого порядка, чем нечеткая переменная, т. е. значениями лингвистической переменной являются нечеткие переменные. Лингвистические переменные предназначены для анализа сложных или плохо определенных явлений. Использование словесных описаний, которыми оперирует человек, делает возможным анализ… Читать ещё >
Аппарат нечетких множеств и описание биообъектов (реферат, курсовая, диплом, контрольная)
Человек способен принимать практически полезные решения в условиях неполной и неопределенной (нечеткой) информации. В связи с этим построение моделей, использующих рассуждения человека, и применение их в компьютерных системах представляет собой одну из важнейших научно-технических проблем. При количественном описании и построении моделей биообъектов и систем для решения конкретных прикладных задач целесообразно, а в ряде случаев и необходимо, использовать указанную способность человеческого интеллекта, с тем чтобы адекватно учесть специфику биообъектов. Мощный инструмент совместного решения этих проблем — математический аппарат, основы которого были разработаны в 1965 г. Лотфи Заде.
В работе Заде «Fuzzy sets» были введены понятие «нечеткое множество» и операции над ними, обобщены известные методы логического вывода. На основе понятия «лингвистическая переменная» и допущения о том, что в качестве значений этой переменной выступают нечеткие множества, был создан аппарат для описания процессов интеллектуальной деятельности, учитывающий нечеткость и неопределенность выражений человеческих суждений и оценок.
Значениями переменных могут быть слова и предложения естественного или формального языка, тогда соответствующие переменные называют лингвистическими. Так, например, среднее значение лингвистической переменной «температура тела человека» iT может принимать следующие значения: «низкая», «нормальная», «повышенная», «очень высокая» (рис. 10.3).
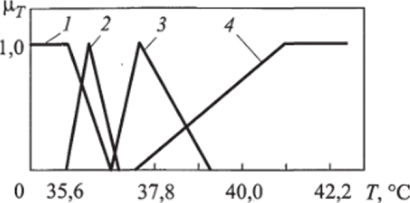
Рис. 10.3. Зависимость среднего значения лингвистической переменной «температура тела человека»:
1 — низкая; 2 — комфортная; 3 — повышенная; 4 — высокая Лингвистическая переменная — это переменная более высокого порядка, чем нечеткая переменная, т. е. значениями лингвистической переменной являются нечеткие переменные. Лингвистические переменные предназначены для анализа сложных или плохо определенных явлений. Использование словесных описаний, которыми оперирует человек, делает возможным анализ систем настолько сложных, что они недоступны обычному математическому описанию.
Структура лингвистической переменной описывается набором (N, Т, X, G, Д/), где N — название переменной; Т — терммножество N, т. е. совокупность значений лингвистической переменной (нечетких переменных); X — универсальное множество с базовой переменной х, G — синтаксическое правило, которое может быть задано в форме бесконтекстной грамматики, порождающей термы-множества Т М — семантическое правило, которое каждому значению / лингвистической переменной ставит в соответствие его смысл Л/(/), обозначающий нечеткое подмножество множества X.
Значения лингвистической переменной — нечеткие множества, символами которых могут быть слова и предложения в естественном или формальном языке, служащие, как правило, некоторой элементарной характеристикой явления.
Язык можно рассматривать как соответствие между термоммножеством Т и универсальным множеством X. Это соответствие характеризуется нечетким называющим отношением N из Т в X, которое связывает с каждым термином t в множестве Т и каждым элементом х в множестве X степень применимости термина t к элементу jc. Такое соответствие называют функцией принадлежности.
Для фиксированного термина t функция принадлежности определяет нечеткое подмножество M (t) из множества X, которое является смыслом или значением термина /. Таким образом, значение термина t есть нечеткое подмножество M (t) из множества X, для которого термин t служит символом.
Термин может быть элементарным, например: «/ = высокий», или составным, когда он представляет собой сочетание элементарных терминов, например: «t = очень высокий».
Более сложные понятия могут характеризоваться составной лингвистической переменной. Например, понятие «человек» может рассматриваться как название составной лингвистической переменной с компонентами «возраст», «рост», «вес», «внешность» и т. п.
Базовая переменная лингвистической переменной «возраст» является по. своей природе числовой. У лингвистической переменной «внешность» не имеется четкой базовой переменной. В этом случае функцию принадлежности задают не на множестве математически точно определенных объектов, а на множестве обозначенных некими символами впечатлений.
Следует отметить, что благодаря использованию принципа обобщения большая часть существующего математического аппарата, применяющегося для анализа систем, может быть адаптирована к нечетким и лингвистическим переменным с числовой базовой переменной. Во втором случае способ обращения с лингвистическими переменными носит более качественный характер.
Нечеткая логика является многозначной, что позволяет установить промежуточные значения для таких общепринятых оценок, как да/нет, истинно/ложно, черное/белое. Такие выражения, как «слегка тепло» или «довольно холодно», можно сформулировать математически и, что крайне важно, программировать и обрабатывать на компьютерах.
Эффективность систем нечеткой логики базируется на следующих теоремах.
1. В 1992 г. Ванг доказал теорему: для каждой вещественной непрерывной функции G (x), .заданной на компакте U, и для произвольной величины г > 0 существует нечеткая экспертная система, формирующая такую выходную функцию F (x), что sup || F (x) — G (x) ||< 8, где ||…|| - символ нормы. Другими словами,.
xeU
для каждой вещественной непрерывной функции (7(дс) можно построить нечеткий аппроксиматор с заданной погрешностью аппроксимации.
2. Согласно теореме FAT (Fuzzy Approximation Theorem), доказанной Б. Коско в 1993 г., любая математическая система может быть аппроксимирована системой, которая основана на нечеткой логике.
Системы нечеткой логики целесообразно применять:
- • для сложных процессов (биопроцессов), не допускающих построение «обычных» прогностических динамических моделей;
- • когда экспертные знания об объекте или о процессе можно сформулировать главным образом в вербальной форме (особенно актуально для биомедицинских информационных систем).
Различия между четкими и нечеткими множествами целесообразно рассмотреть на примерах.
Пусть Е — четкое универсальное множество; х — элемент множества Е R — некоторое свойство подмножества А универсального множества Е, элементы которого удовлетворяют свойству R, определяется как множество упорядоченных пар А = {тА(х)1х}у где тА(х) - отношение, называемое характеристической функцией, тА(х) = 1, если х удовлетворяет свойству /?, и тА(х) - 0 — в противном случае.
Например, имеется множество Е всех чисел х от 0 до 10. Определим подмножество А множества Е всех действительных чисел от.
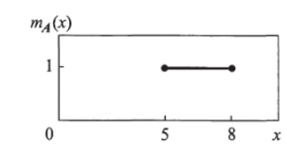
Рис. 10.4. Характеристическая функция принадлежности четкого множества.
5 до 8: закрытый интервал А = [5, 8]. Свойство R элементов подмножества А - выполнение условия 5 < х < 8. Характеристическая функция подмножества А ставит в соответствие число 1 или 0 каждому элементу в множестве X в зависимости от того принадлежит данный элемент подмножеству А или нет (рис. 10.4).
Нечеткое подмножество отличается от четкого тем, что для элементов х из множества Е нет однозначного ответа да/нет относительно выполнения свойства R. В связи с этим нечеткое подмножество А универсального множества? определяется как множество упорядоченных пар:
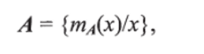
где гпа (х) — характеристическая функция принадлежности, принимающая значения в некотором вполне упорядоченном множестве М (например, М= [0, 1]). Функция принадлежности указывает степень (или уровень) принадлежности элемента х подмножеству А. Множество М называют множеством принадлежностей. Если М = = {0,1}, то нечеткое подмножество А может рассматриваться как четкое множество.
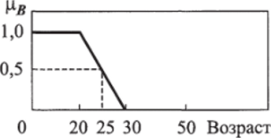
Рис. 10.5. Пример характеристической функции принадлежности нечеткого множества В.
Например, пусть В = {множество молодых людей}. Нижний предел этого множества строго нуль, тогда как верхний предел точно определить нельзя, поскольку невозможно строгое (четкое) разделение на молодых и немолодых людей. Однако можно задать некоторый диапазон значений возрастов по признаку «еще не стар, но уже не молод». Так, разумно считать, что все люди моложе 20 лет — молодые, а старше 30 — немолодые. Тогда характеристическая функция, описывающая степень принадлежности человека с данным возрастом к множеству молодых людей В, может быть такой, как на рис. 10.5 (здесь степень принадлежности множеству молодых людей для возрастов (20 < возраст < 30) изменяется линейно).
Для формализации субъективного смысла качественных показателей экспертам предлагают различные функции принадлежности.
г / /ч Линейная функция принадлежности ру>(х)=^—^—ур (рис. 10.6, а) задается посредством установления экспертом значений /2 и /].
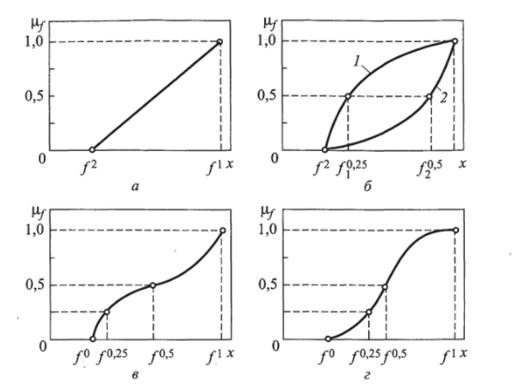
Рис. 10.6. Линейная (о), экспоненциальные 1,2 (б), гиперболическая (в) и обратная гиперболическая (г) функции принадлежности нечеткого множества Экспоненциальная функция принадлежности записывается как Ру (х) = а jl-exp | (рис. Ю.6, б), где b — параметр формы; /" - значение функции / (х), соответствующее степени принадлежности а.
Гиперболическая функция принадлежности (рис. 10.6, в) имеет вид р^(х) = 0,5tg (a/(x) —[1]/) + 0,5 (а — параметр формы; d — точка инфлексии), обратная гиперболическая функция принадлежности (рис. 10.6,г) — py (x) = arctg (a/(x);
В пакете MatLab Fuzzy Logic реализованы следующие характеристические функции (рис. 10.7):
• треугольная trimf (х, a, b, с) = max (min ———, ——-, 0);
yb-a с-Ь)
• гауссова.
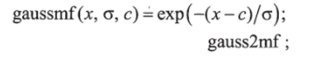
• двойная гауссова.
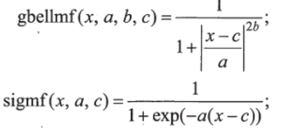
- • обобщенная колоколообразная
- • сигмоидальная
- • двойная сигмоидальная sigmf;
- • произведение двух сигмоидальных функций dsigmf;
- • Z-функция zmf;
- • S-функция smf;
- • Pi-функция pimf.
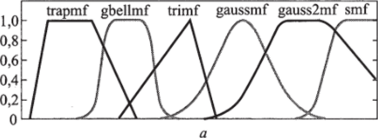
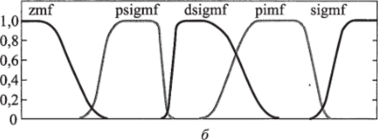
Рис. 10.7. Варианты (а, б) функций принадлежности в MatLab Fuzzy Logic
Разработаны различные методы построения функций принадлежности нечетких множеств.
Прямые методы определения функции принадлежности реализуются, когда эксперт задает значение Цд (х) для каждого х е Е либо определяет вид характеристической функции. Как правило, прямые методы используются для измеримых понятий, таких как, например, скорость, время, давление, температура, или же при выделении полярных значений. К прямым методам также относятся прямые групповые методы экспертных оценок, когда группе экспертов предъявляют конкретный объект, и каждый эксперт должен указать, принадлежит ли данный объект множеству А. Функция принадлежности данного объекта определяется как отношение числа утвердительных ответов к общему числу экспертов.
Косвенные методы задания функции принадлежности используются в случаях, когда не существует элементарных измеримых свойств, через которые определяется данное нечеткое множество. Как правило, это методы попарных сравнений. При известных значениях функции принадлежности (например, хА(х,) = щ, i = 1, 2, п) попарные сравнения могут быть представлены матрицей отношений, А = {<�яу}, где я, у = uy/wy.
На практике эксперт сам формирует матрицу А, при этом диагональные элементы равны единице (ан =1), а элементы, симметричные относительно диагонали, — а, у = 1/я, у Например, если один фактор оценивается в к раз сильнее чем другой, то последний фактор должен быть в 1/к раз сильнее, чем первый. В общем случае задача сводится к поиску собственного вектора и>, удовлетворяющего уравнению вида А* = /тахи', где l^x — наибольшее собственное значение матрицы А. Поскольку матрица А, по определению, положительна, то решение данной задачи существует и положительно.
Нечеткий кластерный анализ. Задача нечеткого кластерного анализа формулируется следующим образом: на основе матрицы исходных данных D требуется определить такое нечеткое разбиение R (A) = {А/1А/ с А } множества Л = {а, аг, …, я"} на заданное число К нечетких кластеров, которое доставляет экстремум некоторой целевой функции f (R (A)) среди всех нечетких разбиений.
В качестве алгоритма кластеризации в нечеткой задаче, как и в однозначной, можно применять алгоритм К внутригрупповых средних, состоящий из определенных шагов.
Шаг 1. Предварительное задание значения исходных кластеров К. Например, при диагностике ранних артритов пациентов разбивают на четыре группы: норма, ранний (РА), подагрический (ПА) и псориатический (ПсА) артриты. Затем указывают максимальное количество итераций, а также экспоненциальный вес расчета целевой функции и центров кластеров т.
В качестве текущего нечеткого разбиения на первой итерации алгоритма для матрицы данных D следует задать некоторое исходное нечеткое разбиение на с непустых нечетких кластеров, которые описываются совокупностью функций принадлежности Мв");
Для исходного текущего нечеткого разбиения рассчитывают центры нечетких кластеров:
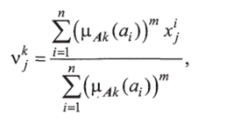
где x’j — элемент кластера.
Шаг 2. Формирование нового нечеткого разбиения исходного множества А на К непустых нечетких кластеров, характеризуемых совокупностью функций принадлежности ц*(а,).
Шаг 3. Продолжение выполнения алгоритма по описанной выше схеме, пока число пройденных итераций не превысит значение s.
На рис. 10.8, а приведены результаты обработки данных с помощью алгоритма К внутригрупповых средних для однозначной задачи диагностики ранних артритов, при этом явно выделен только один класс — группа здоровых пациентов. На рис. 10.8, б показаны результаты нечеткого кластерного анализа при диагностике ранних артритов — явно заметны центры четырех кластеров и отслеживается граница между множествами.
- [1] трапецеидальная trapmf (х, a, b, с, d)=max (minf 7—^, 1, 1 0); Ib-a c-d)