Нелинейные системы автоматического регулирования прерывистого действия с релейными элементами

Релейные системы автоматического регулирования относятся к категории систем регулирования прерывистого действия. По своему принципу действия релейные системы вследствие нелинейной характеристики релейных элементов являются нелинейными системами. В релейных системах замыкание и размыкание цепи регулирования происходит в зависимости от значения регулируемой величины. Эти моменты времени заранее не известны и поэтому не могут быть заданы извне.

Релейные системы автоматического регулирования можно разделить на релейные астатические {прерывистые астатические) и позиционные. В астатических прерывистых релейных системах контур обратной связи периодически замыкается и размыкается с помощью реле. Позиционные регуляторы обеспечивают перемещение регулирующего органа в одно из фиксированных положений или позиций. По количеству возможных позиций различают двух-, трехи многопозиционные регуляторы.

Релейные астатические регуляторы. На рис. 4.44, а в качестве примера приведена релейная система автоматического регулирования уровня жидкости в резервуаре. Эта система регулирования аналогична астатической системе регулирования, показанной на рис. 1.12, но только разность напряжений на двух движках потенциометра R подается теперь не на якорь сервомотора М, а на обмотку поляризованного реле Р. Его средний подвижный контакт в зависимости от знака отклонения регулируемой величины замыкается с верхним или нижним неподвижными контактами, подавая на якорь сервомотора М напряжение U положительной или отрицательной полярности. В результате получается либо одно, либо другое направление вращения сервомотора М, увеличивающее или уменьшающее подачу жидкости <2,. Нейтральному положению среднего контакта реле соответствует значение выходного напряжения U, равное нулю.

Зависимость выходной величины реле от входной величины называется статической характеристикой реле. Идеальная статическая характеристика реле показана на рис. 4.44, б, а реальная характеристика с зоной нечувствительности — на рис. 4.44, в. Кроме зоны нечувствительности реальные статические характеристики имеют форму петли гистерезиса. Такие характеристики будут показаны ниже.

Двухиозиционные регуляторы. Рассмотрим процессы в схеме на рис. 4.44, а при идеальной релейной характеристике без зоны нечувствительности и без петли гистерезиса. Такой релейный регулятор называют двухпозиционным регулятором.

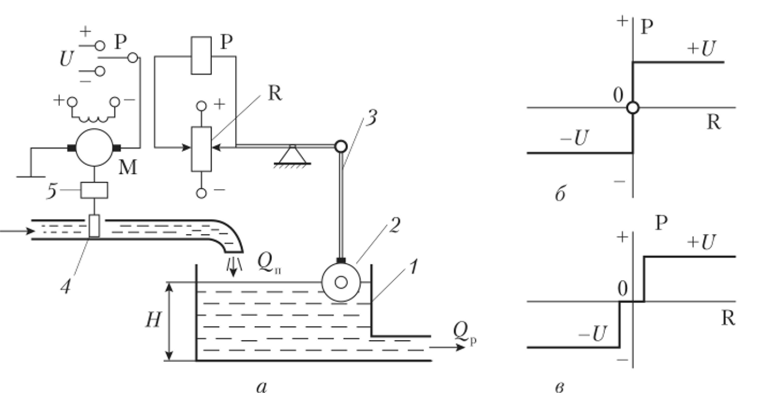
Рис. 4.44. Релейная астатическая система автоматического регулирования уровня жидкости в резервуаре.

Ход процесса регулирования в релейных системах регулирования определяют следующим образом. Считают, что все звенья системы, кроме реле, имеют линейные характеристики. Составляют уравнения динамики линейной части системы. При известных начальных условиях решают составленную систему уравнений, присоединяя к ней уравнение реле, например, для замкнутого верхнего контакта. Решение ведут до тех пор, пока не замкнется нижний контакт. В качестве начальных условий для этого участка берут данные, полученные в конце предыдущего участка. Такой метод нахождения решения для процесса регулирования в релейной системе называют методом припасовывания. Однако такой метод достаточно трудоемок, и поэтому проще находить решение, используя метод математического моделирования.

На рис. 1.13 и 1.14 было показано решение уравнений, описывающих процесс регулирования в линейной системе с астатическим регулятором (рис. 1.12). На рис. 4.45 приведено решение уравнений, составленных для релейной астатической системы регулирования, показанной на рис. 4.44, а. Эта система уравнений отличается от рассмотренной ранее (рис. 1.13) только тем, что второе уравнение в ней нелинейное, отражающее статическую характеристику реле с помощью функции знака sign. Вместо самого отклонения у₀ берется его знак:

+ 1, если уровень жидкости стал меньше заданного;

— 1, если уровень жидкости стал больше заданного.

Из рис. 1.13 следует, что в системе второго порядка при изменении расхода возникают колебания. При введении в схему релейного регулятора с идеальной статической характеристикой колебания практически исчезают (рис. 4.45).

Рис. 4.45. Решение системы уравнений, описывающих релейную систему регулирования в интегрированном пакете MathCad. Характеристика реле идеальная (рис. 4.44, б):

верхняя кривая — уровень Н жидкости в резервуаре (10 — /г"); нижняя кривая — уменьшенный в 10 раз расход жидкости (Qp (f")/10).

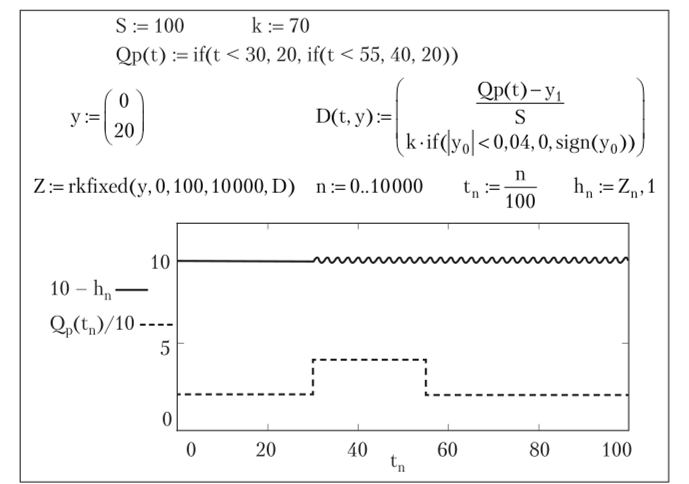
Рис. 4.46. Решение системы уравнений, описывающих релейную систему регулирования в интегрированном пакете MathCad. Характеристика реле имеет зону нечувствительности (рис. 4.44, в):

верхняя кривая — уровень Я жидкости в резервуаре (10 — h"); нижняя кривая — уменьшенный в 10 раз расход жидкости (Qp (f_n)/10).

Если характеристика реле имеет зону нечувствительности (рис. 4.44, в), то колебания в системе усиливаются (рис. 4.46). Здесь зона нечувствительности задается функцией с условием if.

Двухпозиционный релейный регулятор рассмотрим на простом примере релейной системы поддержания постоянной температуры на регулируемом объекте, который испытывает возмущающее воздействие F (рис. 4.47). Здесь двухпозиционный регулятор работает как переключатель, который либо включает нагреватель на полную мощность, либо полностью отключает его. Такой широко распространенный двухпозиционный регулятор прост в эксплуатации и обеспечивает хорошие регулировочные свойства.

Рис. 4.47. Функциональная схема двухпозиционной системы регулирования температуры.

Для предотвращения слишком частого включения и отключения нагревателя напряжения срабатывания и отпускания реле отличаются друг от друга, и характеристика реле имеет форму прямоугольной петли гистерезиса (рис. 4.47). Ширина зоны гистерезиса настраивается при наладке системы регулирования. На рис. 4.48 приведена математическая модель двухпозиционной системы регулирования температуры в пакете визуального математического моделирования Simulink матричной математической системы MATLAB. Как уже говорилось выше, модели в этой среде называют S-моделями.

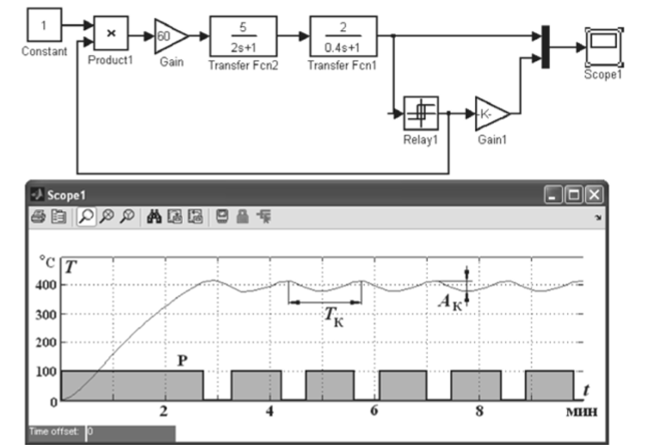
Рис. 4.48. S-модель в пакете Simulink двухпозиционной системы регулирования температуры.

Контакты реле замыкаются и включают нагреватель при температуре менее 390 °C, а размыкаются по достижении температуры 410 °C. Процесс с двухпозиционным регулированием при поддержании постоянной температуры, как следует из рис. 4.48, является автоколебательным. Показателями автоколебательного режима являются амплитуда Л_к и частота /_к или период Т_к автоколебаний (рис. 4.48).

Трехпозиционные регуляторы. Трехпозиционную релейную систему автоматического регулирования рассмотрим на примере регулирования напряжения. Одним из основных показателей качества электроэнергии, регламентированных стандартом, является допустимое отклонение напряжения от его номинального значения. Многие приемники электрической энергии весьма чувствительны к отклонениям напряжения, могущим привести к тяжелым последствиям. Поэтому в электрических сетях с изменяющимся напряжением необходимо иметь регуляторы, которые поддерживали бы напряжение на определенном заданном уровне.

Рассмотрим прежде всего трехпозиционную релейную систему автоматического регулирования напряжения в системах электропитания небольшой мощности. В качестве силового регулирующего органа может быть использован автотрансформатор или трансформатор Т с тремя отводами 1, 2,3 на вторичной стороне трансформатора (рис. 4.49). Напряжение на вторичной стороне трансформатора, к которой подключена нагрузка Н, может изменяться при изменении питающего напряжения или при изменении самой нагрузки. Будем считать, что изменяется первичное, т. е. питающее напряжение. Процессы будут происходить аналогично и при изменении нагрузки.

Приемники электроэнергии, получающие питание от трансформатора, согласно стандарту, допускают определенные отклонения напряжения, например ±5% или ±10%. Поэтому не обязательно поддерживать питающее напряжение строго равным номинальному. Достаточно того, чтобы напряжение не выходило за указанные пределы. Если питающее напряжение на первичной стороне трансформатора номинальное, то потребители должны подключаться к отводу 2, рассчитанному на номинальное напряжение. Если напряжение повышенное, то следует подключить потребителей к отводу 1, понижающему напряжение. Если же напряжение пониженное, то потребители должны подключаться к отводу 3, повышающему напряжение. Для этого к отводу 2 подключены два реле Р1 и Р2, настроенные на разные напряжения срабатывания (см. рис. 4.49), а нагрузка Н подключается к нужному отводу трансформатора в зависимости от состояния этих реле в соответствии с табл. 4.7.

Статическая характеристика реле показана на рис. 4.49, б, из которого следует, что напряжение срабатывания {/, первого реле Р1 меньше, чем напряжение срабатывания U_2cp второго реле Р2. Напряжения срабатывания обоих реле не совпадают с их напряжениями отпускания t/_loTII и f/_2oxn. Статическая характеристика реле имеет форму петли гистерезиса.

Нелинейные функции скачкообразного изменения выходных характеристик реле, показанные на рис. 4.49, б, имеющие разрывные характеристики, будут в этом случае представлять собой графические изображения уравнений реле как нелинейных звеньев данной системы регулирования. Переключения реле Р1 и F2 происходят при определенных значениях напряжения, которое является контролируемой величиной. Для подключения нагрузки к нужному отводу трансформатора служат контакты контакторов К1 и К2, которыми управляют реле Р1 и Р2.

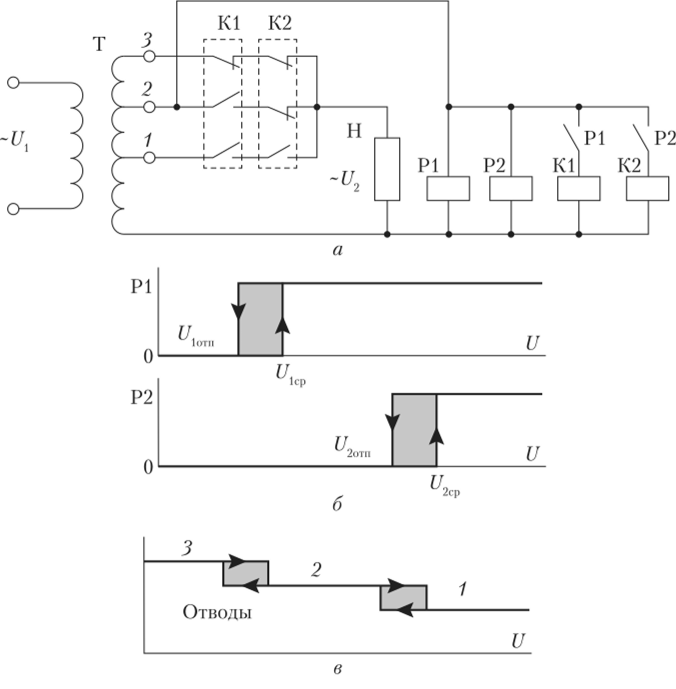
Рис. 4.49. Схема трехпозиционного релейного регулятора напряжения (а), статические характеристики реле Р1 и Р2 (б) и характеристика переключения отводов (в).

Логика работы рассматриваемого релейного регулятора (см. рис. 4.49 и табл. 4.7) следующая. Если напряжение стало меньше, чем напряжение f/_1oTtl, то оба реле Р1 и Р2 находятся в несработавшем состоянии, их нормально замыкающиеся контакты в цепи контакторов К1 и К2 разомкнуты. Через нормально замыкающиеся контакты контакторов К1 и К2 нагрузка Н подключается к отводу 3, повышающему напряжение. Условие подключения нагрузки к отводу 3 записывается так:

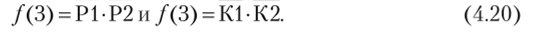
Если напряжение повысится и сработает первое реле Р1, то размыкающиеся контакты К1 разомкнутся, а замыкающиеся — замкнутся, и нагрузка отключится от отвода 3 и подключится к отводу 2. Условие подключения к отводу 2 имеет вид.

При дальнейшем повышении напряжения оба реле Р1 и Р2 срабатывают, и нагрузка Н отключается от отвода 2 и подключается к отводу 7, понижающему напряжение. Условие подключения к отводу 1 записывается следующим образом:

Состояния реле.

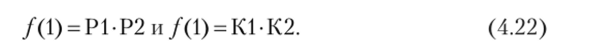
Таблица 4.7

Силовую часть схемы, представленной на рис. 4.49, можно преобразовать и упростить, если использовать переключающиеся контакты контакторов К1 и К2 (рис. 4.50). В этом случае исключается ошибочное одновременное подключение нагрузки к двум отводам и повышается эксплуатационная надежность регулирующего устройства.

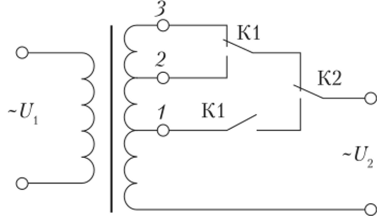
Рис. 4.50. Преобразованная схема регулирующего органа.

На рис. 4.51 приведена S-модель трехпозиционного релейного регулятора напряжения в пакете Simulink системы MATLAB. Первичное напряжение U_x задается как сумма двух напряжений: постоянного 220 В и переменного, изменяющегося (для простоты) но синусоидальному закону. Может быть задан и любой другой закон изменения входного напряжения. Для реализации логических функций (4.20)—(4.22) использованы обычные блоки математического умножения, поскольку логическое умножение (функция И) и математическое умножение единичных функций дают одинаковые результаты. Но результат математического умножения единичных функций можно усилить с помощью усилителя Gain. Логический же сигнал усилить с помощью усилителя невозможно. Логический сигнал может быть или только нуль, или только единица. Он не может быть, например, равным 1,1. На рис. 4.52 приведена осциллограмма напряжений трехпозиционного релейного регулятора.

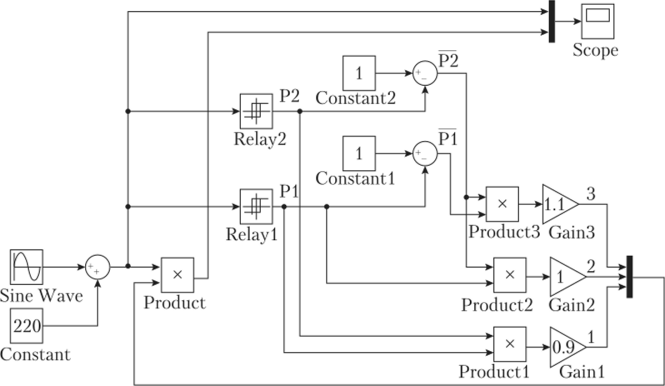
Рис. 451. S-модель трехпозиционного релейного регулятора напряжения.

В модели, приведенной на рис. 4.51, параметры настройки реле Р1 и Р2 следующие (см. рис. 4.49): П_1ср = 220 В, ?/_2отп = 210 В, t/_2cp = 240 В, t/_2oTI1 = 230 В.

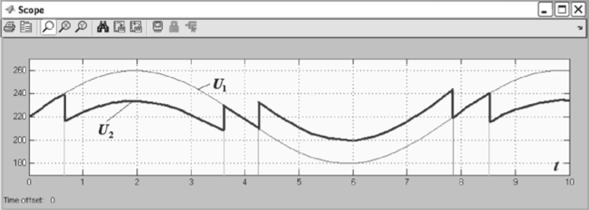
Рис. 4.52. Осциллограмма напряжений трехнозиционного релейного.

регулятора На рис. 4.53 приведена S-модель, а на рис. 4.54 осциллограмма напряжений трехпозиционного регулятора напряжения с источником случайного сигнала с равномерным распределением Uniform Random Number. Этот источник служит для генерации сигнала с равномерным распределением. Уровень сигнала генератора ограничен сверху и снизу значениями Maximum и Minimum, которые задаются в окне редактирования параметров генератора. В модели заданы напряжения: Maximum = 260 В, Minimum = 180 В.

Настройки реле Р1 и Р2 такие же, как и в модели на рис. 4.51. Цифрами на рис. 4.54 показаны номера отводов трансформатора при автоматическом регулировании напряжения. Как следует из рис. 4.52 и 4.54, при использовании простого трехпозиционного релейного регулятора колебания напряжения U₂ на нагрузке существенно уменьшаются.

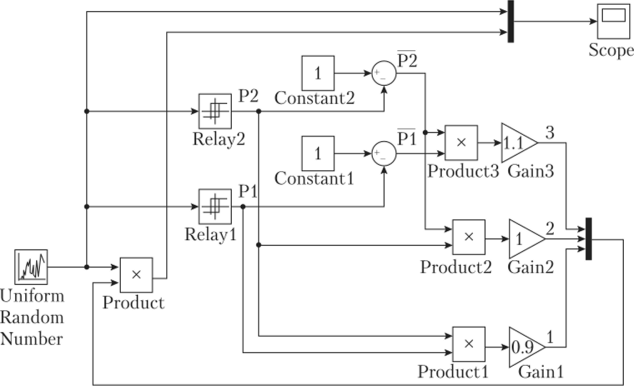
Рис. 453. S-модель трехпозиционного релейного регулятора напряжения с источником случайного сигнала.

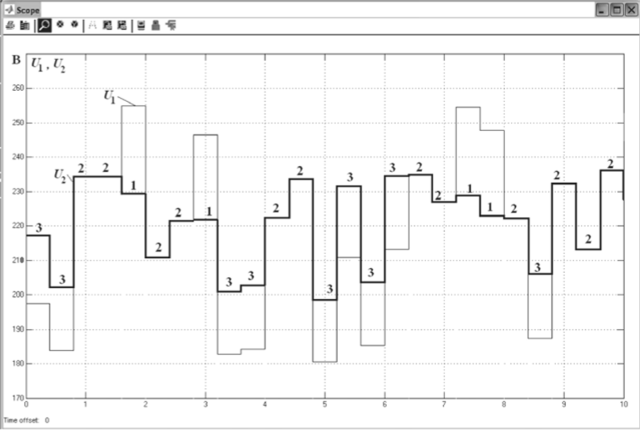
Рис. 454. Осциллограмма напряжений трехпозиционного релейного регулятора с источником случайного сигнала.

Многоиозиционные регуляторы. Многопозиционные релейные системы автоматического регулирования рассмотрим также на примере автоматического регулирования напряжения.

В мощных питающих сетях к отклонениям напряжения предъявляются более жесткие требования. Поэтому силовые трансформаторы снабжают специальными устройствами регулирования напряжения, которые имеют порядка 10 ответвлений в сторону понижения напряжения и столько же ответвлений в сторону повышения напряжения. Ответвления выполняются с шагом коэффициента трансформации около 2%. Такое исполнение регуляторов повышает точность регулирования и улучшает показатели его качества. С помощью специальной конструкции, которую здесь мы не рассматриваем, ответвления могут переключаться под напряжением, не вызывая перерыва электроснабжения потребителей. При этом скользящий контакт, соединенный с нагрузкой, переходит без разрыва цепи с одного отвода трансформатора на другой, соседний, отвод (рис. 4.55).

Логика работы такого многопозиционного регулятора проста. Если напряжение увеличилось выше допустимого заданного предела, то надо перейти на отвод, уменьшающий напряжение, т. е. подать сигнал на уменьшение напряжения. При этом скользящий контакт переместится на нижележащий отвод. Если же напряжение уменьшилось, то надо перейти на отвод, увеличивающий напряжение, т. е. подать сигнал на увеличение напряжения. При этом скользящий контакт переместится на вышележащий отвод.

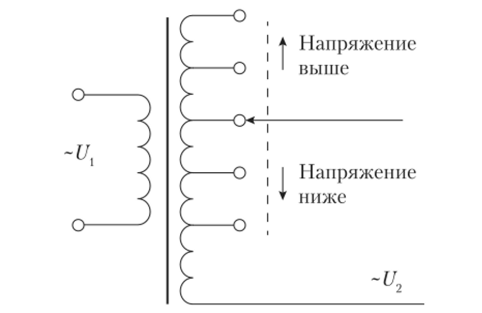
Рис. 4.55. Принцип регулирования напряжения питающих трансформаторов.

Не приводя принципиальной схемы регулятора с электромеханическим приводом, в которой скользящий контакт, соединенный с нагрузкой, переходит без разрыва цепи с одного отвода трансформатора на другой, соседний, отвод, проанализируем работу такого многопозиционного регулятора напряжения с помощью математической модели, составленной в интегрированном пакете MathCad. Программа для исследования модели приведена на рис. 4.56.

Программа представляет собой функцию, записанную в виде последовательности отдельных простых шагов (строк) из программных операторов, связанных друг с другом и объединенных общей вертикальной чертой. Символ <�— является оператором локального (внутреннего) присвоения. Такое присвоение действует только в теле программного модуля. Вне модуля такое присвоение игнорируется и считается, что его не было. Оператором for задается цикл с фиксированным числом повторений. Это значит, что несколько выражений, объединенных вертикальной чертой в подпрограмму, будут повторяться заданное число раз для переменной k от 0 до t. Оператор if проверяет выполнение заданного условия и производит действие, указанное в выражении только в том случае, если условие выполняется. Если же условие не выполняется, то не выполняется и указанное действие. В качестве выходной величины программного модуля по умолчанию берется значение его последней строки. В последней строке программы стоит функция объединения четырех векторов одинакового размера — augment (Т, ul, u2, N).

Рис. 4.56. Математическая модель многопозиционного регулятора напряжения, записанная в виде программы в пакете MathCad.

Параметрами функции расчета Reg, которые задаются пользователем, являются:

U — действующее значение номинального напряжения; d — значение напряжения одной ступени отводов в долях от номинального;

t — время расчета.

В программе приняты следующие обозначения параметров: u 1 — питающее напряжение;

и2 — напряжение, подаваемое потребителю электрической энергии;

N — коэффициент трансформации в относительных единицах.

На рис. 4.57 приведены осциллограммы автоматического регулирования напряжения при ступени регулирования напряжения d = 0,1 (10%), а на рис. 4.58 — при d = 4%.

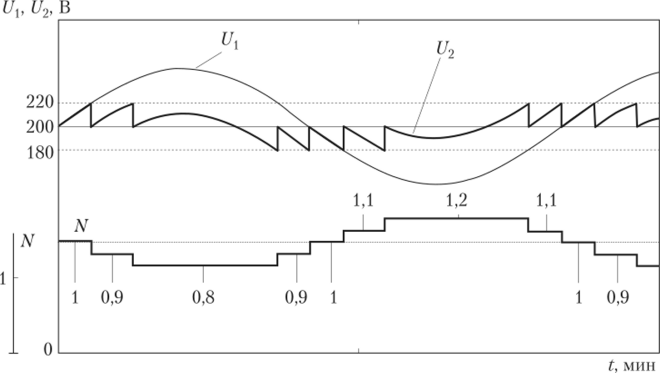
Рис. 4.57. Осциллограмма напряжений многопозиционного релейного регулятора. Ответвления трансформатора составляют 10% от номинального напряжения.

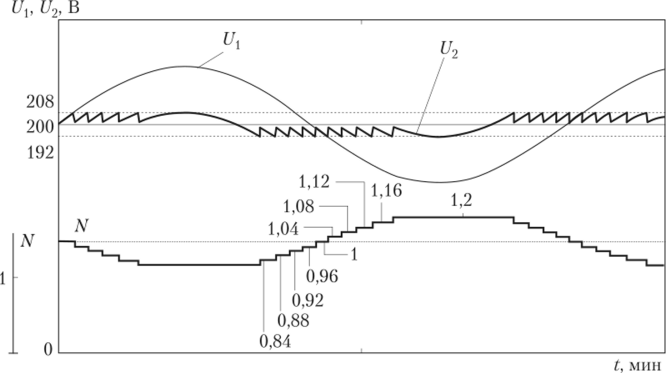
Рис. 4.58. Осциллограмма напряжений многопозиционного релейного регулятора. Ответвления трансформатора составляют 4% от номинального напряжения.

Из рис. 4.57 и 4.58 следует, что при d = 4% напряжение поддерживается точнее. Однако в этом случае получается большее количество переключений, что может вызвать преждевременный износ переключающего устройства. Поэтому на практике ограничивают число переключений отводов в течение суток на уровне 20—25 переключений, применяя так называемое адаптивное регулирование. Для этого предварительно анализируют возможные отклонения — их среднее значение и дисперсию, закладывая эти данные в программу и вводя определенные выдержки времени. Более подробно узнать об адаптивных регуляторах можно в [27].