Устранение сечения в подструктурных дедуктивных мультикатегориях

Для подструктурной дедуктивной мультикатегории G мы можем сконструировать свободную подструктурную дедуктивную мультикатегорию Fr (G), порожденную G. Объекты этой мультикатегории получаются индуктивно из объектов G с помощью операций ®, л, v, /, ±. Ее секвенции получаются из секвенций G путем присоединения базисных секвенций l_A, и т. д., и формирования новых операций из старых с помощью правила сечения и правил (®), (-)_р и т. д. Тождества между сравнимыми секвенциями в Fr (G) будут те и только те, которые следуют из тождеств в G, и мультикатегорные тождества.

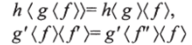
Помимо этого, добавляются еще и тождества 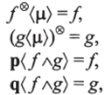и т. п., рассмотренные ранее.

Ранее уже было рассмотрено понятие мультифунктора для случая экспоненциальных дедуктивных мультикатегорий. Расширим теперь это понятие на случай подструктурных дедуктивных мультикатегорий.

Определение 1. Подструктурный мультифунктор F из подструктурной дедуктивной мультикатегории М в подструктурную дедуктитвную мультикатегорию М' представляет собой мультифунктор, сохраняющий структуру мультикатегорий, т. е. выполняются следующие условия: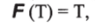

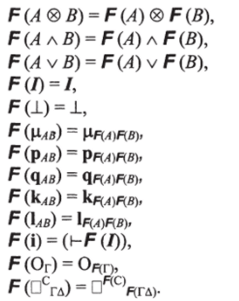
Здесь для простоты не делается различия между константами и операциями первой и второй мультикатегории.

Пусть U будет стирающим мультифунктором, тогда подструктурный мультифунктор G—>C/F (G) будет, как известно, полным и точным [Lambek 1993] (полнота свидетельствует о том, что мультифунктор не порождает никаких новых секвенций по сравнению со старыми, а точность свидетельствует об отсутствии новых тождеств между секвенциями).

Теорема устранения сечения принимает теперь следующий вид:

Теорема 1 (устранение сечения). Если стрелки р, р, q, k, 1 заменить на правила (®), (-)_р, (-), (-)*, (-)/, то любая секвенция в UF (G), сконструированная с помощью правил сечения, будет эквивалентна секвенции, сконструированной без применения правила сечения.

Доказательство. Без потери общности допускаем, что стрелки /: ЛК Л и g: ГАЛЬ В уже были получены без применения правила сечения. Позднее покажем, что g (J) эквивалентна секвенции, в конструировании которой были вовлечены сечения меньшей «степени», причем степень сечения g{f) определяется как.

где d (A) есть число вхождений всех связок в А и d (F) = d{A) + … + + d (A_m). Возможны следующие случаи:

• 0. И/и g содержатся в G.
• 1. На последнем шаге конструирования /вводится одна связка по левую сторону стрелки.
• 2. На последнем шаге конструирования g вводится одна связка по левую сторону стрелки, но не в А.
• 3. На последнем шаге конструирования g вводится одна связка по правую сторону стрелки.
• 4. На последнем шаге конструирования и/и g вводится одна связка в А.

В случае 0 стрелка g (j) уже содержится в мультикатегории G, замкнутой относительно сечения. Рассмотрим теперь по очереди остальные случаи.

(1). Связка ®.

Случай 1. Пусть Л = Г’А'® В’А' и/=/'*. В этом случае мы имеем:

Заменим это выражение на:

где новое сечение имеет меньшую степень. Более того, имеет место g (f '*> = (g</'"^e, что можно показать во внутреннем языке. На место переменной типа А'®В' мы можем поставить ух’у', где х' и у' являются переменными типа А' и В' соответственно. Нетрудно убедиться, что

проверяя, что обе стороны сводятся к gufu’x’y’v’v, используя определения () и ®.

Случай 2. Пусть Г = Г‘А'®В'А' и / = /'*. (Случай, когда Д= Г’А'®В'А' такой же, поэтому он будет опущен) Мы имеем:

Заменим это выражение на:

где новое сечение имеет меньшую степень. Более того,.

поскольку обе стороны сводятся кf’u 'x'y'v'fwv.

Случай 3. В = А'®В' и g — fo®f: Г’Д'(- А'®В'. Допустим, что А содержится в Г'. (Случай, когда оно появляется в Д' аналогичен и будет опущен) Мы имеем:

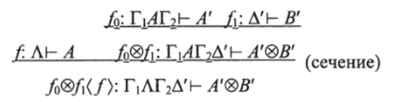
Заменим это выражение на:

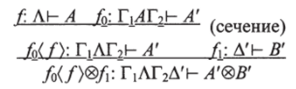
где новое сечение имеет меньшую степень. Более того,.

поскольку обе стороны сводятся к if_auJwu₂fv’ввиду определений.

(®)и<).

Случай 4. В = А'®В' и g =fo®f nf=g'®. Мы имеем 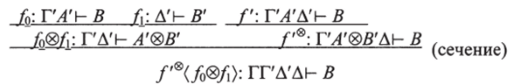Заменим все это на:

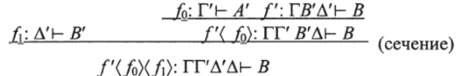
где оба новых сечения имеют более низкую степень. Более того,.

что можно рассматривать следующим образом. Левая часть выражения сводится к /'®Mp/o"/ivV ввиду определений (®) и (). Теперь мы используем тот факт, что / =/а это затем сводится к /.

'uf_au’fv’v, которое также представляет собой то, к чему сводится правая часть ввиду определения ().

(2). Связка л.

Случай 1. Пусть Л = Л|Л'лВ'Л₂ и/=Мы имеем:

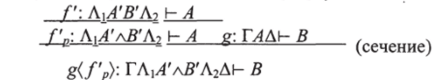
Заменим это выражение на:

где новое сечение имеет меньшую степень. Более того, если /'есть переменная типа А’л.В', то.

так как обе стороны сводятся к guf’w>t V₂v, используя определения Ои/V.

Случай 2. Пусть Г = Г^А'лВ'Гг и g = g'_p. Мы имеем:

Заменим это выражение на:

).

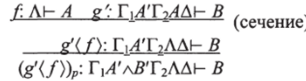где новое сечение имеет меньшую степень. Более того,.

поскольку обе стороны сводятся к gt/ip/'Mj/wv так же как в случае 1. Случай 3. В = Л’лВ' и g = go*g- Мы имеем.

Заменим это выражение на.

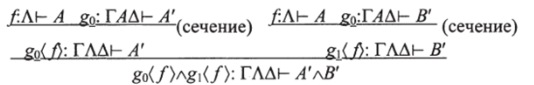
где оба новых сечения имеют меньшую степень. Более того,.

(и аналогично для q), так как левая сторона сводится к 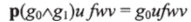так же как и правая.

Случай 4. Пусть А = А’лВ',/ = /ол/i и g = g_р. Мы имеем:

Заменим это выражение на.

где новое сечение имеет меньшую степень. Более того,.

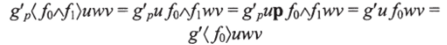
(3). Связка V.

Случай 1. Л = PiAvB’A' и f=foyf- Мы имеем:

Заменим это выражение на:

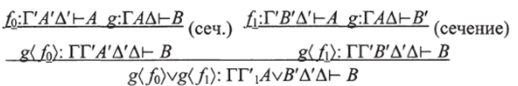
где оба новых сечения имеют меньшую степень. Более того,.

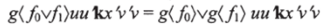
(то же самое имеет место, если мы заменим кх’на 1у), поскольку обе стороны сводятся к guf₀u’xVV.

Случай 2. Пусть Г = f’A’vB’A' и пусть g = go^gi? Мы имеем:

где оба новых сечения имеют меньшую степень. Более того,.

govg," кг 'v W = go{f)vg{fi wkcVW.

(то же самое имеет место, если мы заменим 1у' на кх ?), поскольку обе стороны сводятся к gou 'х V 'fwv.

Случай 3. В = A’vB' и g = g¹*. Мы имеем.

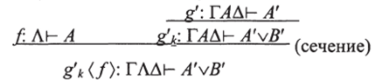
Заменим это выражение на.

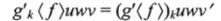
где новое сечение имеет меньшую степень. Более того, поскольку обе стороны сводятся к kg 'иfwv.

Случай 4. А = A’vB', f=f и пусть g = g₀vg|. Мы имеем.

Заменим это выражение на:

где оба новых сечения имеют меньшую степень. Более того, govgi (/*)wwv = govgiHk/'wv = gouf’wv = g₀(f')uwv.

(4). Нульместная связка I. Заметим, что Случай 3 невозможен. Случай 1. А = Г7Д' и/=/". Мы имеем:

Заменим это выражение на: где новое сечение имеет меньшую степень. Более того, 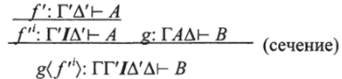и.

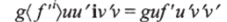
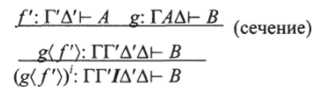
сводятся к тому же самому выражению.

Случай 2. Г = Г7Д' и пусть g = g" . Мы имеем:

Заменим это выражение на:

где новое сечение имеет меньшую степень. Более того,.

Случай 3. А = J, f = i и пусть g = g" . Мы имеем:

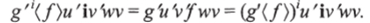
Очевидно, что g" (i) = g 'может быть построено без сечения.

(4). Нульместная связка _L. Возможны только два случая.

Случай 1. Мы имеем:

Заменяем все это построение на стрелку ?: ГГ'_1_Д'Д (- В, сконструированную без сечения, и отметим, что g (D) = ?.

Случай 2. Пусть Г = Г'±Д'. Мы имеем:

Заменяем все это на стрелку ?: Г’З-Д'ЛДьС, сконструированную без сечения, и отметим, что? = ?. ?