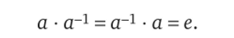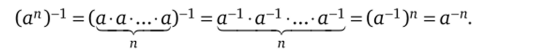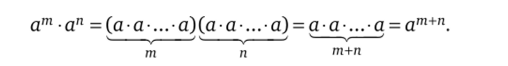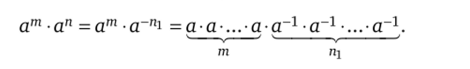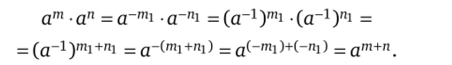Основные свойства групп

Докажем основные свойства групп, используя мультипликативную терминологию. Пусть дана группа (G, •).

1. Единица группы единственна.

Доказательство. Пусть е и е_х — единицы группы G. Поскольку е — единица группы, то е? е_г = е_ь а так как е_г — единица группы, то е • е₁ = е. Следовательно, е, = е.

2. Для каждого элемента группы обратный элемент единственен.

Доказательство. Пусть а е G и элементы b, с е G являются обратными для а. Это означает, что ab = Ьа = е и ас = са = е. Используя это и ассоциативность умножения, получаем Ъ = Ъ? е = = Ь (а ? с) = (Ь а)? с = е • с = с.

3. Для любых a, b е G уравнения а-х-Ъиу-а-Ъ однозначно разрешимы.

Доказательство. Рассмотрим уравнение а? х = Ь.

Существование решения. Легко проверить, что х₀ = а^-1 • b является решением данного уравнения.

Единственность решения. Пусть х₁нх₂ — решения уравнения а? х = Ь. Тогда ах₁ = Ьиа-х₂ = Ь, откуда а • х_а = а? х₂. Умножим равенство слева на а^-1 и, воспользовавшись свойством ассоциативности, получим х_г = х₂.

Уравнение у • а = Ь рассматривается аналогично.

4. Обратный элемент для произведения двух элементов находится по формуле (ab)^-1 = Ь^-1а^-1.

Доказательство. (аЬ)(Ь^-1а^-1) = а (ЬЬ^-1)а^-1 = аеа^-1 = аа^-1 = е.

5. Обратный элемент к обратному равен самому элементу: (сг¹)^-1 = а для любого, а е G.

Доказательство. Это свойство вытекает из равенства.

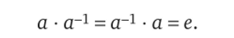
Определение 1.5. Для любого элемента а е G положим а⁰ = е. Для любого натурального числа п будем считать, что а^п = а а-…-а и а~^п = (а^-1)". Выражение а^п, где п е Z, называется.

П

степенью (элемента а с целым показателем).

• 6. Свойства степеней.
• 6.1. (а^п)^-1 = а~^п для любого, а е G и любого п е Z. Доказательство. Для любого натурального п имеем

Отсюда (а-'¹)^-1 = а^п - сг⁽-^п).

6.2. а^т ? а^п = а^т+п для любого, а е G и любых т, п е Z. Доказательство. Рассмотрим все возможные случаи относительно целых тип:

а) т, п е N, тогда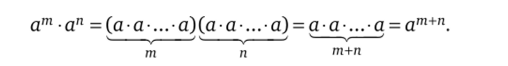

• б) Если хотя бы один из показателей т, п равен нулю, то доказываемое равенство очевидно.
• в) Пусть те N, п = -п_ь где nj е N. Тогда

Если mvто ответом будет (а^-1)'^!1^-т =cr⁽ⁿi^_m) -а~^пi^+m -а^т+п. Если т — п_г, то получим а⁰ -а^т~^пi =а^т+п. Если же п_г < т, то будем иметь а^т~^пi -а^т+п.

Случай пе N, т — -т_ь где m_t е N, сводится к рассмотренному.

г) Пусть т = -т_ь п = -п_ь где т_ь п_г е N. Тогда.

6.3. Для любых т, п е Z (а^т)" = а^тп.

Упражнение 1.4. Докажите свойство 6.3 самостоятельно, рассмотрев все возможные случаи относительно целых показателей тип.