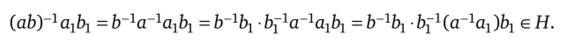Факторгруппа. 
Алгебра и теория чисел. 
Группы, кольца и поля

Рассмотрим множество всех левых смежных классов группы G по подгруппе Я. Естественно попытаться определить умножение левых смежных классов формулой аН? ЪН — аЪН для любых а, Ъ е G. Но для этого нужно, чтобы элемент b всегда можно было переставить через Я. Это возможно лишь в случае, когда Я является нормальной подгруппой.

Пусть теперь подгруппа Я нормальна в группе G. Тогда всякий левый смежный класс gH равен правому смежному классу Hg и можно говорить просто о смежных классах по нормальной подгруппе Я. Докажем, что в этом случае резутьтат аН? ЪН = = аЪН не зависит от выбора представителей смежных классов. Пусть аН = а, Я, ЬН = Ь, Я. Докажем, что аН? ЬН — а^Н ? Ь, Я. Для этого нужно доказать, что аЪН = а^Ъ_гН, а это равносильно условию (аЬУ¹а₁Ь₁ е Я. Поскольку аН = а_хН, ЬН = Ь_}Н, то а~^га_} е Я, b~¹b j е Я. Используя нормальность подгруппы Я, получаем.

Таким образом, умножение смежных классов является бинарной операцией, и, как легко видеть, множество всех смежных классов относительно этой операции образует группу (с единицей Я). Она обозначается G/Я (читается: G по Я). Введем название для этой группы.

Определение 1.15. Если Я — нормальная подгруппа группы G, то группа смежных классов G/H называется факторгруппой группы G по подгруппе Я.

Теорема 1.11. Факторгруппа циклической группы циклическая.

Доказательство. Пусть Я — подгруппа группы G = (а). По теореме 1.4 Я = (а^п) при некотором натуральном п. Тогда G/Я = {Я, аН, а²Н, …, а'^Н} = (аН) — циклическая группа. Теорема доказана.

Вместе с тем если нормальная подгруппа Я и факторгруппа по ней G/Я циклические, то группа G не обязана быть циклической. Например, группа подстановок S₃ не является циклической, хотя она имеет циклическую подгруппу Я = А₃— (а), где а = (123), и факторгруппа G/Я = S₃/A₃ = (ЬА₃), где b = (12), является циклической.