Две основные задачи динамики

В динамике решаются две основные задачи:

• 1. По заданному движению точки определить силы, производящие это движение.
• 2. По заданным силам, действующим на точку или систему, определить закон движения точки или системы.

Для несвободной материальной точки, т. е. точки, на которую наложена связь, вынуждающая ее двигаться по заданной поверхности или кривой, первая задача динамики обычно заключается в определении реакции связи. Вторая (основная) задача динамики при несвободном движении точки распадается на две и состоит в том, чтобы, зная действующие на точку активные силы, определить:

• • закон движения точки,
• • реакции наложенной связи.

Обе задачи решаются при помощи уравнений (1.52) и (1.55).

Решение первой задачи динамики

Пусть движение точки массой т задано координатным способом, т. е.

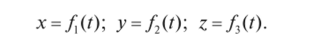
Дифференцируя дважды по t и подставляя значения т, х, у, z в уравнение (1.52), найдем проекции равнодействующей силы на оси координат: F_x = mx F_y=my F_:=m't Модуль и направляющие косинусы равнодействующей определим по известным формулам: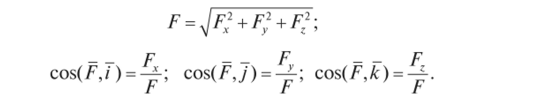

Если движение точки задано естественным способом, т. е. задана траектория и закон движения точки S =/(/) по траектории, то равнодействующую силу найдем по уравнениям (1.55).

Определяем.

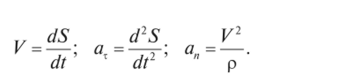
Подставляем найденные значения в уравнения (1.55):

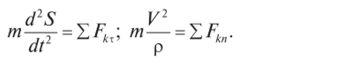
Находим проекции равнодействующей на касательную и нормаль (см. рис. 1.71). Модуль и направление равнодействующей определим по формулам:

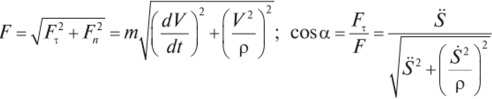
где а — угол, образованный равнодействующей с положительным направлением касательной к траектории точки.

Задача. Точка массой т кг движется в плоскости Оху (рис. 1.72). Уравнение ее движения в прямоугольных декартовых координатах x = acoskt, y = as kl (хиу — в метрах, / — в секундах), а и к — постоянные. Найти силу, действующую на точку.

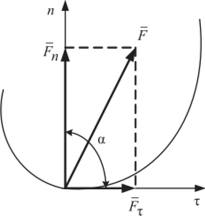
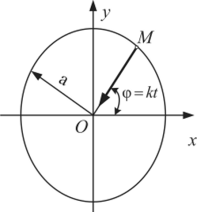
Рис. 1.71 Рис. 1.72.

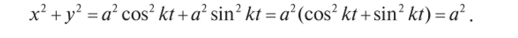
Решение:

• Исключив параметр t, найдем уравнение траектории:

Следовательно, траектория — окружность радиуса а с центром в начале координат.

_п d²x d²y

• Для нахождения силы вычислим —г, —г •.

dr dt

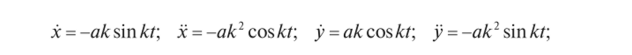
V = ijx² +у² = ак м/. Подставим эти значения в дифференциальные уравнения движения точки в прямоугольных декартовых координатах: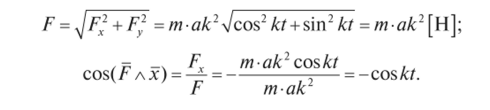

Модуль силы.

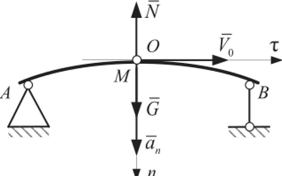
Сила F направлена к центру окружности.

Следовательно, равномерное движение точки по окружности происходит под действием постоянной по модулю силы, направленной к центру окружности. Как известно, эта сила называется центростремительной.

Отметим, что при решении первой задачи динамики дифференциальные уравнения движения (1.52) и (1.55) интегрировать не приходится.

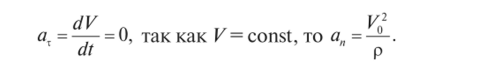
Задача. Автомобиль массой т движется с постоянной скоростью V₀ по выпуклому мосту, имеющему в вертикальном сечении форму дуги окружности радиуса р. Определить давление автомобиля на мост в момент прохождения им середины моста (рис. 1.73).

Рис. 1.73 Решение: Рассмотрим автомобиль как материальную точку. Так как известна его траектория, то воспользуемся естественными уравнениями движения точки. Найдем проекции ускорения на касательную и нормаль:

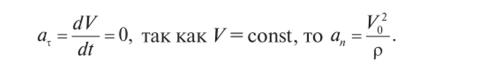
На автомобиль действуют две силы — сила веса G и реакция мо;

— — Ун? К ~

ста N. Из формулы (1.55) получим: F_t=m a.= 0; F"=-— = G-N, от;

Р куда N = G——. Мы нашли не давление автомобиля на мост, а ре;

Р акцию моста. Но по третьему закону Ньютона давление автомобиля.

fyi. у~

на мост равно реакции моста. Следовательно, TJ = N = G—— и на;

Р правлена вниз.