Двухфакторный дисперсионный анализ

Рассмотрим дисперсионный анализ влияния двух факторов А и В на изменчивость признака X. Пусть факторы А и В имеют соответственно по к

и / уровней, при каждом сочетании которых получено по п значений величины X. Тогда число возможных сочетаний уровней этих факторов равно И, а общее число наблюдений значений признака N= kin.

При анализе влияния двух факторов А и В на признак X имеем следующие источники изменчивости:

• 1) фактор А ;
• 2) фактор В;
• 3) взаимодействие факторов Л и В (под взаимодействием факторов будем понимать их одновременное действие);
• 4) неучтенные случайные причины.

Для установления влияния этих факторов изменчивости вычислим:

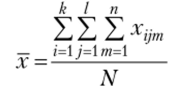 — общее среднее значение признака;

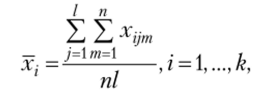 — средние значения признака на уровнях фактора А;

— средние значения признака на уровнях фактора В;

— средние значения признака при различных сочетаниях уровней факторов А и В.

Назовем разности: х#_т —х — 11-_т — общим эффектом, х_х -х = Д — эффектом i-го уровня фактора Д х_}-х- Д — эффектом j-го уровня фактора В, Xjj — х = Сjj — смешанным эффектом факторов, А и В, х-_т -х^ =Z^_m — случайным эффектом.

Таким образом, смешанный эффект x_i} —х является суммой эффектов, полученных под влиянием i-ro уровня фактора А и j- го уровня фактора В и их взаимодействия на этих уровнях. Чтобы вычислить эффект ДД взаимодействия факторов при у-м сочетании их уровней, вычтем из смешанного эффекта эффекты Д и Д. Тогда эффект взаимодействия.

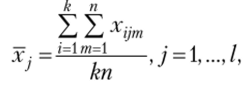
или, учитывая, что Д -х_х -х, Д — х-_} -х, получим ДД = х + х, у -х_х -х_у

Любой общий эффект Щ_т можно представить в виде суммы составляющих его эффектов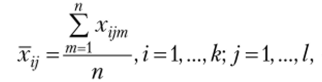

Нетрудно убедиться, что суммы определенных выше эффектов равны нулю, т. е.

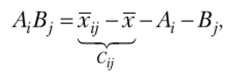
где X обозначает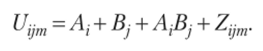

Можно показать, что.

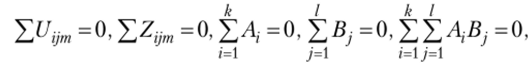
Левая часть формулы (10.3) представляет сумму квадратов общих эффектов, которая обозначается Q, первая сумма в правой части — взвешенная сумма квадратов эффектов фактора Л (Q_A), второе — взвешенная сумма квадратов эффектов фактора В (Q_B), третье — взвешенная сумма квадратов эффектов взаимодействия факторов Q_AB, четвертое — сумма квадратов случайных эффектов Q_z. Следовательно,.

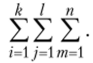
Выведем формулы для вычисления этих величин:

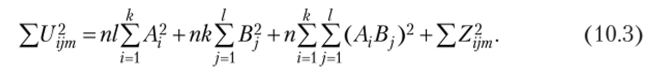
Если обозначить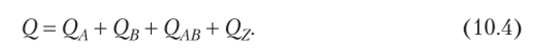

Аналогично получаем формулы для вычисления Q_A, Q_B, Q_A& Q/.

• обозначим 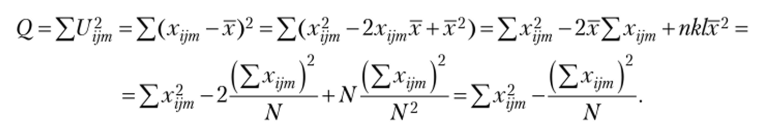, тогда ;

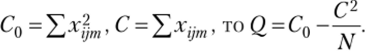• обозначим 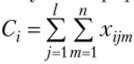, тогда ;

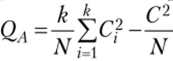• обозначим 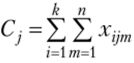, тогда ;

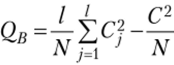• и, наконец,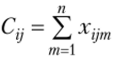

Можно убедиться в выполнении равенства (10.4), подставив в него полученные выражения сумм квадратов эффектов.

Поскольку N общих эффектов связаны соотношением Yj^ijm = 0, ^ ^ЭФ" .

фектов фактораА — соотношением 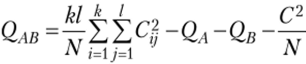эффектов фактора В — соотношением 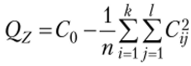эффектов взаимодействия — / соотношениями вида.

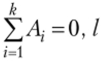и k соотношениями вида 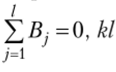, из которых одно является следствием остальных в силу условия 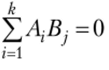случайных эффектов — соотношением вида 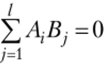, то MQ = (N — 1) а², MQ_A =.

= (k — l)^, MQ_B = (I — 1) g², MQ_ab = (k-l)(/ - 1) g², MQ_z = (N-kl)G². Поэтому суммы квадратов Q, Q_A, Q_B, Q_AB, Qy имеют соответственно следующие числа степеней свободы: V = N — 1, V_A = k — 1, V_B = l — 1, = &/-(& +.

+ / - 1) = (k — 1)(/- 1), F_z= (AT — A/) = ife/(n- 1).

Очевидно, что V = У_л + V_B + + v*

Найдя суммы квадратов эффектов и соответствующие им числа степеней свободы, получим дисперсии признака на одну степень свободы, которые мы ранее называли исправленными дисперсиями:

• общая дисперсия: ;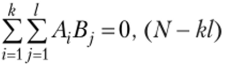

• дисперсия по фактору А: 1 ;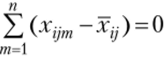

• дисперсия по фактору В: ;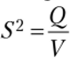

• дисперсия взаимодействия факторов: S_B = ^^лв;

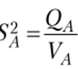
^ав.

• случайная дисперсия,.

Схема двухфакторного дисперсионного анализа.

1. По вышеуказанным формулам вычисляем суммы квадратов эффектов.

Q, Qa> Qb> Qab* Qz;

• 2. Определяем соответствующие числа степеней свободы V, V_A, V_B, V_AB, Vz-
• 3. Вычисляем исправленные дисперсии.

4. Вычисляем величины 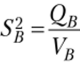, и с помощью критерия Фишера проверяем гипотезу Н₀ относительно каждого источника изменчивости.

5. Вычисляем величины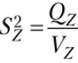

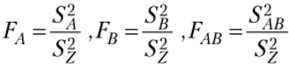и по ним судим об удельном весе каждого источника изменчивости признака в их общей совокупности.

Замечание 10.6. Если гипотеза Я₀ о равенстве средних отклоняется, то сравнение средних по уровням факторов выполняется при помощи ?-статистики Стьюдента с соответствующим числом степеней свободы.

Пример 10.2. В супермаркете разработаны три варианта расположения торговых секций. Каждый вариант испытывается в течение недели (при одном выходном дне) с каждым из пяти выделенных ассортиментных наборов товаров. Данные о дневной выручке магазина в проведенных испытаниях, где фактор А (расположение секций) имеет три уровня, соответствующих вариантам 1, 2, 3, фактор В (ассортиментный набор) — пять уровней, соответствующий занумерованным ассортиментным наборам представлены в таблице.

По схеме двухфакторного дисперсионного анализа исследуем влияние указанных факторов на выручку магазина.

Решение. Чтобы упростить вычисления, уменьшим все исходные данные на 17 и затем умножим на 10, получим следующую таблицу:

Найдем суммы квадратов эффектов, учитывая, что k = 3, / = 5, п = б, N= 90:

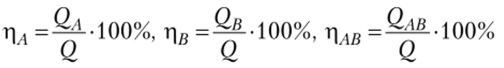
Легко проверить, что равенство (10.4) выполнено.

Определяем соответствующие числа степеней свободы: V_A = 2, V_B = 4, V_AB = 8, V_z= 75.

Вычисляем исправленные дисперсии: S_A =5320, S_B =5645, =908, S =222.

Вычисляем величины = 24,0, F_B = 25,4, F_AB = 4,1. С помощью критерия Фишера проверяем гипотезу Н₀ относительно каждого источника изменчивости. Для этого сравним наблюдаемые значения с найденными из таблицы критическими значениями F_Ta6l при, а = 0,05, V_z = 75 и V, равном числу степеней свободы суммы квадратов эффектов, обусловленному каждым источником изменчивости:

при V_A = 2 F_Ta6,(0,05; 2; 75) = 3,13;

при V_B = 4 F_Ta6l(0,05; 4; 75) = 2,5;

при = 8 F_Ta6l(0,05; 8; 75) = 2,08.

Все наблюденные значения превышают соответствующие значения F_Ta6jI. Таким образом, дисперсионный анализ выявил существенное влияние на выручку магазина как самих факторов Л и Л, так и их взаимодействия.

Вычисляем величины г|_л= 18,6, г_в = 39,5, У]_АВ= 12,7, r_z= 29,2. Таким образом, доля влияния фактора Л составляет 18,6%, В — 39,5%, ЛВ — 12,7%, неучтенных случайных факторов — 29,2%.

Так как установлено существенное влияние факторов на изменчивость признака, нужно исследовать значимость его средних на отдельных уровнях.

Найдем средние значения признака на каждом из трех уровней Л Л₂, Л₃ фактора Л. Учтем, что мы уменьшили данные на 17 и затем увеличили в 10 раз, поэтому.

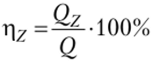
Получаем х_А{ =21,0; х_л<1 =22,4;Т, ц =23,6.

Для определения значимого различия средних на уровнях вычисляем статистики 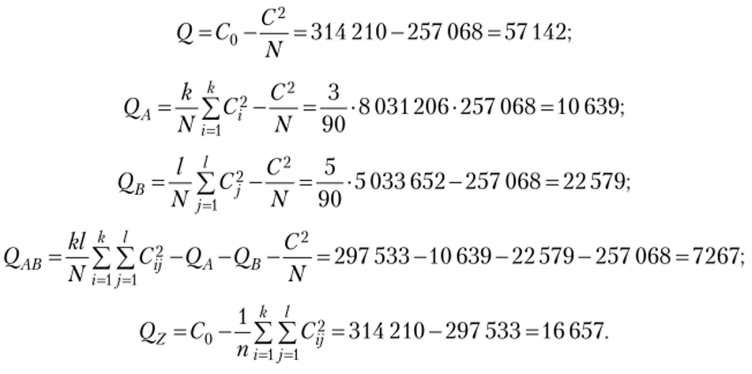(при этом имеем в виду преобразование данных, поэтому S_z= 1,49):

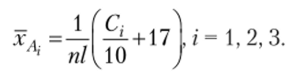
Из таблицы критических точек распределения Стьюдснта при, а = 0,05, V_z = 75 имеем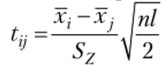

Так как |t₁₂|, $, |^з1 > ^0,05″ ^то можно сделать вывод о существенном влиянии на выручку магазина каждого варианта расположения секций.

Аналогично можно вычислить средние значения признака на каждом уровне В_и В₂, В₃, В₄, В₅ фактора В по формуле.

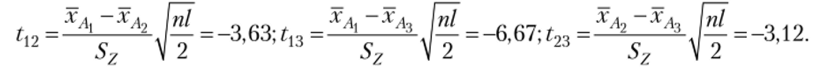
Имеем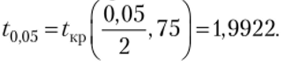

Вычисляем статистики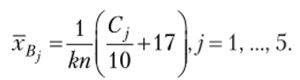

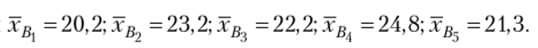
Таким образом, нет оснований считать, что ассортиментные наборы под номерами 3 и 5 дают магазину различные выручки. Остальные пары ассортиментных наборов дают выручку, существенно различающуюся между собой.

Чтобы исследовать взаимодействие факторов, вычислим средние значения.

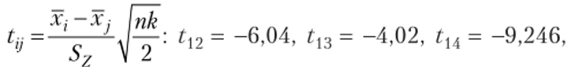
Вычислим статистику 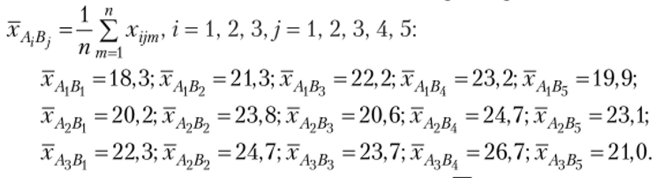при различных сочетаниях средних значений.

Сравнивая полученные значения статистики t с критическим значением.

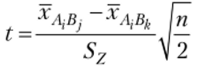делаем вывод, что нет оснований считать выручку существенно различной:

• • при первом варианте расположения секций между 1 и 5, 5 и 2, 3 и 2, 3 и 4 ассортиментными наборами;
• • втором варианте расположения секций между 1 и 3, 5 и 2, 5 и 4, 2 и 4 ассортиментными наборами;
• • третьем варианте расположения секций между 1 и 5, 1 и 3, 3 и 2 ассортиментными наборами;
• • первом ассортиментном наборе между 1 и 2 вариантами расположения секций;
• • втором ассортиментном наборе между 2 и 3 вариантами расположения секций;
• • третьем ассортиментном наборе между 1 и 2, 1 и 3 вариантами расположения секций;
• • четвертом ассортиментном наборе между 1 и 2 вариантами расположения секций;
• • пятом ассортиментном наборе между 1 и 3 вариантами расположения секций.

Все остальные значения выручки различаются значительно. Кроме того, получено, что при втором варианте расположения секций значительно большую выручку дает пятый ассортиментный набор по сравнению с третьим и при пятом ассортиментном наборе — второй вариант расположения секций по сравнению с третьим.