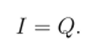Синтаксические меры информации

Чтобы измерить информацию на синтаксическом уровне (не учитывая ни смысловое содержание, пи важность передаваемой информации), рассматриваются два параметра: объем данных Q и количество информации I.

Объем данных Q в сообщении определяется только для дискретных сообщений и в общем случае измеряется количеством символов (букв, цифр или иных знаков) в этом сообщении. Например, объем авторского печатного листа составляет Q₀.a. =.

= 40 000 символов (знаков).

В большинстве случаев передаваемые символы кодируются числами, которые могут быть записаны в различных системах счисления. Один и тот же разряд в разных системах счисления имеет различный вес. Так, второй разряд в десятичной системе счисления имеет вес 10² = 100, а в двоичной системе счисления — 2² = 4. При переходе от одной системы счисления к другой меняется, соответственно, и единица измерения объема данных:

• — для двоичной системы счисления такой единицей является бит (англ, bit — сокращение от binai’y digit двоичный разряд);
• — троичной системы счисления — трит;
• — десятичной системы счисления — дит.

Например, сообщение, представленное числом в двоичной системе счисления как 10 100 011, имеет объем данных Q = 8 бит. Сообщение 839 126, представленное числом в десятичной системе счисления, имеет объем данных Q = G дит.

Группа из 8 битов называется байтом. Однако, так как бит и байт слишком маленькие единицы объема данных, то для измерения реальных объемов передаваемых и хранимых данных используют более крупные единицы.

Согласно ГОСТ 8.417−2002 «Государственная система обеспечения единства измерений. Единицы величин» в РФ с 1 сентября 2003 г. должны использоваться единицы измерения информации, приведенные в табл. 1.1.

Использование приставок СИ (кило-, мега-, тера-, пета-, экса-, зетаи йота-) к единицам, кратным 2, в соответствии с этим стандартом является некорректным. Данные приставки следует использовать только для обозначения 10³, 10°, 10⁹, 10¹², 10¹⁵, 10¹⁸, 10²¹ и 10²⁴ соответственно.

Единицы измерения информации

Таблица 1.1

В ряде задач, например, при передачи данных по сети или кодировании аудиои видеоинформации используют единицы, выраженные через биты: килобит (Кбит), мегабит (Мбит), гигабит (Гбит) и т. д. В соответствии с указанным выше ГОСТом, 1 Кбит = 1000 бит, 1 Мбит = 1000 Кбит, 1 Гбит = 1000 Мит и т. д.

Невозможность определить количество информации / на синтаксическом уровне без рассмотрения понятия неопределенности состояния источника информации, в качестве которого может выступать объект, явление, процесс, событие, система приводит к понятию специальной характеристики неопределенности, называемой энтропией.

Рассмотрим энтропию, а следовательно, и количество информации более подробно. Пусть имеется источник информации (сообщений), который в каждый момент времени случайным образом может принять одно из конечного множества возможных состояний. Обозначим этот источник информации через X = {жьаъ,. .ялг}, ^гД^е N — число равновозможных (равновероятных) состояний источника. Подчеркнем, что для описания степени неопределенности источника совершенно неважно, какие именно значения rci, X2,… Тдг записаны; важно только количество этих значений.

Изменение степени неосведомленности получателя информации тесно связано с процессом ее получения. Пусть об источнике X до получения информации пользователь имел предварительные (априорные) сведения. Обозначим меру осведомленности пользователя как функцию Н (Х) — энтропию источника (мера неопределенности состояния).

После того, как к получателю поступило сообщение 6*, он приобрел дополнительную информацию 1₈(Х). В результате априорная неосведомленность уменьшилась так, что апостериорная (после получения сообщения 6*) неопределенность о состоянии источника стала Ii (X/s).

Если, например, априорная неосведомленность об источнике была равна 5 единицам, а после поступления сообщения s апостериорная неосведомленность Н (Х) об источнике, допустим, стала равной 3 единицам, тогда количество информации об источнике /Дх), полученной в сообщении s, будет определено как.

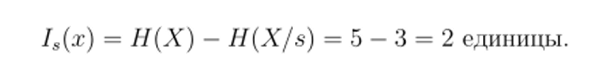
Таким образом, изменение (точнее, уменьшение) неопределенности состояния источника определяет количество информации.

Если после получения сообщения неопределенность II (X/s) стала равной 0 (неопределенность отсутствует), то для получателя неполное знание заменится полным знанием. При этом количество информации станет равным I_s(x) = Н (Х). Например, если в мешке находится пять шаров с различными номерами, то, вынув из мешка один шар и определив его номер, можно на 1/5 сократить неопределенность, а после выемки пятого шара неопределенность снимается полностью, так как все номера шаров становятся известными.

Итак, процесс получения информации рассматривается как выбор одного сообщения из конечного наперед заданного множества N равновероятных сообщений. В результате такого выбора, а следовательно, уменьшения числа возможных вариантов (т.е. неопределенности), в конечном итоге получим полную информацию, которая не оставляет вариантов вообще. Следовательно, энтропия Н (Х), понимаемая как мера, неопределенности состояния источника X, моэ/сст. рассматриваться как мера количества информации, когда полностью устранена неопределенность относительно его состояния.

Чем больше возможностей выбора, т. е. чем больше число N возможных состояний источника, тем больше неопределенность выбора, а значит, тем меньше информации содержится в сообщении о конкретном состоянии источника.

Для сообщения о том, что произошло одно из N равновероятных событий, количество информации /, содержащейся в этом сообщении, вычисляется по формуле.

Данная мера количества информации была предложена в 1928 г. американским ученым Р. Хартли.

Выражение (1.1) применяется для оценки количества так называемой индивидуальной информации, получаемой путем снятия исходной неопределенности в результате произошедшего события или для оценки количества информации, приходящееся на одно состояние системы (количество информации в событии о состоянии системы).

Выбор основания логарифма в (1.1) определяет един иду измерения количества информации и принципиального значения не имеет. Обычно основание выбирают равным 2, так как именно столько устойчивых состояний имеют элементы, на которых базируются современные СВТ. При этом (1.1) примет вид.

В случае использования формулы (1.2) единицей измерения количества информации является бит. 1 бит равен количеству информации, которое содержит сообщение, уменьшающее неопределенность знаний в два раза. Согласно (1.2) при 1=1 имеем N = 2, поэтому говорят, что сообщение несет 1 бит информации, если произошло одно событие из двух возможных.

Таким образом, 1 бит с точки зрения теории информации — это количество информации, необходимое дчя различения двух состояний источника информации. В вычислительной технике в качестве таких состояний выбирают устойчивые состояния элементов, используемые дчя внутреннего представления данных и команд. Эти состояния обозначаются как Он 1. Величина 1 бит с точки зрения вычислительной техники — наименьшая единица памяти, необходимая для хранения одного из двух значений.

Пример 1.2. Пусть имеется колода из 36 карт. Какое количество информации (бит) содержит сообщение о том, что из колоды карт случайным образом достали даму пик?

Решение. В этом случае N — 36. Искомое количество информации рассчитывается по формуле (1.2): / = log₂36 «5 бит. ?

Мера информации (1.2) рассчитана на модель источника информации, для которого все его возможные состояния равновероятны. Вероятность появления события принадлежащего множеству X = {х, х₂,… Хдг} равновозможных событий, определяется выражением.

Используя (1.1), (1.3), выразим количество информации через вероятность:

В действительности для произвольного источника степень неопределенности выбора его состояний зависит не только от числа возможных состояний, но и от вероятности появления (выбора ист, очником) этих состояний. Если состояния источника неравновероятны, то свобода выбора состояний источника ограничивается, что, как следствие, приводит к уменьшению неопределенности.

Пример 1.3. Пусть имеются два источника информации, каждый из которых может находиться в двух различных состояниях. Пусть вероятности нахождения в различных состояниях составят 0,95 и 0,05 для первого источника и 0,5 и 0,5 для второго.

Неопределенность нахождения в некотором состоянии у первого источника значительно меньше, чем для второго, так как для второго источника отсутствуют какие-либо обоснованные предположения о нахождении в некотором состоянии. Следовательно, энтропия первого источника существенно ниже энтропии второго. ?

Пример 1.3 иллюстрирует следующий факт: количество информации в сообщении от источника с большей вероятностью нахождения в каком-либо состоянии будет меньше, чем от. источника с равновероятнылш состояниями.

Вероятность р, появления события А*, принадлежащего конечному множеству X = {xi, x₂,. .хм} неравновозможных событий, определяется на основании большого числа К (К —> ос) проведенных испытаний как отношение числа Ki появления события.

Aj к числу К всех испытаний:

т.е. pi здесь — вероятность того, что произойдет ?'-е событие из полного набора событий, которые вырабатывает источник сообщений.

Если в (1.4) подставить (1.5), то получим выражение количества собственной, или индивидуальной, информации для неравновозможных событий.

Пример 1.4. Пусть вероятность приема символа Х по каналу связи составляет р =.

= 0,01, х₂ — 0,1, гг₃ — 0,15, #4 — 0,25, х*> — 0,49. Определить, какое количество информации несет 4-й символ.

Решение. Используя формулы (1.4) и (1.5), имеем /_г = —log₂0,25 = 2 бит. ?

Среднее количество информации для неравновозможных событий определяется выражением.

где 1{ — количество информации в г-м событии.

Подставив (1.4), (1.5) в (1.6), получаем меру количества информации, предложенную американским ученым К. Шенноном в 1948 г.:

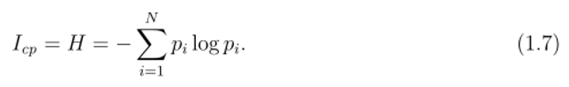
Величину II называют энтропией, которая, согласно выражению (1.7), соответствует количеству информации, приходящемуся на одно испытание, или степени неопределенности, снимаемой после проведения одного испытания. Из (1.7) следует, что энтропия обладает следующими свойствами:

— Н > 0, так как < 1, поэтому logp, < 0;

— Н = 0, когда одна из вероятностей pi = 1, а все остальные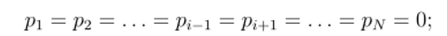

• — энтропия достигает максимального значения Я_тах, когда все вероятности равны
• 1

между собой, т. е. = —. При этом (1.7) вырождается в меру Хартли (1.4). При N = 2 энтропия достигает абсолютного максимума Я_тах = 1;

— энтропия двух независимых множеств А и В событий, образующих полное пространство событий, равна сумме энтропии исходных множеств (свойство аддитивности), Н = На + Я#.

Пример 1.5. Используя условие примера 1.4, найти энтропию.

Релиение. В соответствии с (1.7) энтропия системы равна Я = 0,01 • log₂ 0.01 + 0,1 • log₂ 0,1 + 0,15 • log₂ 0,15 + 0,25 • log₂ 0,25 +.

+ 0,49 • log₂ 0,49 «1,8 бит.

Таким образом, среднее значение количества информации, приходящееся на один символ, равно 1,8 бит. ?

Для случая, когда все состояния системы равновероятны, энтропия системы составит.

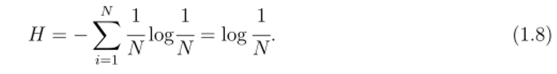
Пусть по каналу связи передастся //-разрядное символьное сообщение. Совокупность используемых символов для формирования любого сообщения называют алфавитом.

Полное число символов алфавита это мощность q алфавита. Возможное число сообщений (кодовых комбинаций) будет N = qⁿ. При равновероятном появлении любого сообщения количество информации, содержащейся в нем, на основании (1.1) равно.

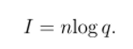
Если по каналу связи передается //-разрядное двоичное сообщение, т. е. q = 2, то количество информации, выраженное в битах, будет равно количеству передаваемых двоичных символов (количеству разрядов):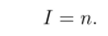

Следовательно, количество информации, содержащееся в двоичном сообщении равно объему данных, полученных по каналу связи: