Маржинальный доход. 
Экономика организации

Ранее мы рассмотрели один из показателей, основанный на расчете частичной себестоимости — валовую прибыль, под которой понимается разница между выручкой за продукцию и суммой прямых затрат на ее производство и реализацию. Но, вообще говоря, на базе частичной себестоимости можно построить разные показатели: все будет зависеть от того, что учитывается в частичной себестоимости.

Валовая прибыль получается как следствие очень удобной формы бухгалтерского учета, однако чисто экономически этот показатель лишен особого содержания, так как совершенно не понятно, что такое в экономическом смысле сумма прибыли и косвенных затрат (а валовая прибыль как раз и представляет собой такую сумму). Дело в том, что деление всех затрат на прямые и косвенные в известном смысле условно и имеет скорее организационную, чем экономическую природу, поэтому показатель, величину которого каждый бухгалтер будет считать по-своему, не очень подходит для серьезного экономического анализа.

В качестве еще одного критерия распределения затрат на учитываемые и не учитываемые при расчете частичной себестоимости может быть отнесение к переменным или постоянным: в себестоимость должны включаться только переменные затраты, а постоянные учитываются отдельно. Поскольку большую часть косвенных расходов можно отнести к постоянным, то этот процесс тоже выглядит как исключение косвенных расходов. Однако для точности расчетов из косвенных затрат надо исключать ту их часть, которую нельзя считать постоянными и добавлять к переменным. Последнее означает, что и в данном случае от процедуры распределения затрат избавиться, как правило, не удается, хотя, конечно, доля распределяемых затрат существенно уменьшается. Но в результате мы получаем показатель, обладающий глубоким экономическим смыслом.

Применительно к одному, отдельно взятому продукту немецкие экономисты называют этот показатель Deckungsbeitrag, что в прямом переводе означает «вклад в покрытие» (англ, contribution margin). Здесь имеется в виду, что данный показатель характеризует вклад рассматриваемого продукта в покрытие суммы постоянных затрат предприятия. В различных изданиях этот показатель называется по-разному, это зависит от того, кто и с какого языка переводил. Встречаются следующие названия: валовая прибыль, маржинальная прибыль, вклад на покрытие, сумма возмещения, маржинальный доход. Очевидно, что этот показатель не является прибылью. Не является он в полном смысле и доходом. В российской практике закрепилось понятие маржинальный доход.

Маржинальный доход = Выручка — Переменные затраты.

Маржинальный доход играет важную роль в экономических расчетах, так как он обладает очень ценным свойством: в широких пределах маржинальный доход на единицу продукции не зависит от объемов выпуска этой продукции. Прибыль таким свойством не обладает.

Пример 7.2.

Предприятие выпускает 1000 шт. изделия по цене 70 руб./шт. и по себестоимости 60 руб./шт. Очевидно, каждое изделие дает 10 руб./шт. прибыли, а общая прибыль равняется 10 тыс. руб. Пусть теперь предприятие сократило производство до 900 шт. при такой же цене. Чему в этом случае будет равняться прибыль?

Огромное количество бухгалтеров и экономистов в этом случае просто пересчитают затраты, используя полученную выше себестоимость, и… будут не правы.

Как при подобном сокращении поведут себя затраты? Можно ли предположить, что в расчете на изделие они останутся неизменными? Очевидно, такое предположение будет справедливо лишь при одном условии: все затраты на предприятии являются переменными, а постоянных нет вообще. Понятно, что так не бывает, поэтому пусть постоянные затраты данного предприятия равны 36 тыс. руб. Это означает, что переменные затраты в расчете на одно изделие составят в данном примере:

(1000 шт. • 60 руб./шт. — 36 тыс. руб.) / 1000 шт. = 24 руб./шт.

Что произойдет, когда объем производства сократится? Очевидно, теперь постоянные затраты будут распределяться на меньший объем продукции, следовательно на 1 шт. будет приходиться: 36 тыс. руб. / 900 шт. = 40 руб./шт.

Поскольку переменные затраты в расчете на изделие не изменились, то теперь себестоимость одного изделия будет равна 40 руб./шт. + 24 руб./шт. = = 64 руб./шт.; штучная прибыль составит 70 руб./шт. — 64 руб./шт. = 6 руб./ шт.; общая прибыль составит 6 руб./шт. • 900 шт. = 5,4 тыс. руб. Таким образом, при уменьшении выпуска на 10% прибыль уменьшилась на 46%.

Но, допустим, экономист сознает, что если объем производства изменился, то изменилась и себестоимость, следовательно, для расчета новой прибыли старые данные о себестоимости уже не годятся. Но где взять новые? Неужели пересчитывать всю себестоимость? А если предприятие производит сотни наименований продуктов?

Иное дело — маржинальный доход. По определению он равен выручке минус переменные затраты, что в расчете на одно изделие составит: 70 руб./шт. — 24 руб./шт. = 46 руб./шт. Поскольку ни цена, ни переменные затраты в расчете на одно изделие не меняются^[1], то не меняется и маржинальный доход от одного изделия.

Сокращение объема производства на 10% — со 1000 шт. до 900 шт. — привело к уменьшению маржинального дохода также на 10% — с 46 тыс. руб. до 41,4 тыс. руб. Чтобы получить прибыль в обоих случаях, надо из маржинального дохода вычесть постоянные затраты. Получим: 46 тыс. руб. — - 36 тыс. руб. = 10 тыс. руб. в первом случае и 41,4 тыс. руб. — 36 тыс. руб. = = 5,4 тыс. руб. — во втором. Эти результаты совпадают с полученными ранее, что и следовало ожидать.

Ранее мы видели, что по величине маржинальный доход равен сумме постоянных затрат и прибыли. В этой связи весьма любопытным представляется вопрос о том, каково соотношение этих составляющих маржинального дохода, например, в рассмотренной только что задаче. Оказывается, что однозначно ответить на этот вопрос невозможно, так как это соотношение все время меняется.

Для того чтобы разобраться в этом, рассмотрим известную задачу о точке безубыточности производства (.break-even point), которая легко решается при помощи маржинального дохода. Пусть выполняются условия предыдущей задачи. Чему в этом случае будет равна точка безубыточности производства?

Производство станет безубыточным в точке, в которой суммарный маржинальный доход станет равным общему объему постоянных затрат предприятия. Сколько изделий должно произвести предприятие в этой точке? Очевидно, чтобы ответить на этот вопрос, надо общую величину постоянных затрат разделить на маржинальный доход каждого изделия.

Таким образом, мы получили известную формулу:

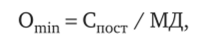
где Omin — объем производства в точке безубыточности в натуральном выражении; Спост — общая сумма постоянных затрат предприятия; МД — маржинальный доход.

Пример 7.2 (продолжение) Для решения сформулированной ранее задачи надо разделить постоянные затраты предприятия на маржинальный доход от выпуска одного изделия, и получим искомый ответ:

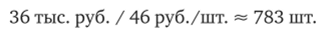
Поскольку точный ответ находится между 782 и 783 шт., то это означает, что при выпуске 782 шт. предприятие еще убыточно, а при 783 шт. — уже прибыльно.

Вернемся к вопросу о соотношении постоянных затрат и прибыли в маржинальном доходе. Легко заметить, что в маржинальном доходе первого, второго и вообще любого изделия, меньшего 782, прибыли нет вообще, так как производство еще не достигает точки безубыточности. Точка безубыточности характеризуется тем, что в ней суммарный маржинальный доход всех изделий в точности равен постоянным затратам предприятия. Но это означает, что за точкой безубыточности, т. е. в данном случае при производстве 784-го, 785-го и т. д. изделий, маржинальный доход уже не содержит постоянных затрат, а состоит целиком из прибыли. Собственно говоря, указанными свойствами в значительной мере и объясняются названия этого показателя: до точки безубыточности весь маржинальный доход — это вклад на покрытие постоянных затрат, за точкой безубыточности каждая дополнительная единица продукта приносит дополнительную прибыль в размере маржинального дохода.

Иными словами, до 782-го изделия производство каждого следующего вносило вклад в покрытие постоянных затрат предприятия в размере 46 руб., а начиная с 784-го изделия каждое следующее увеличивает прибыль предприятия на те же 46 руб.

Понятно, что если взять некое среднее изделие, то (если у предприятия есть прибыль) его маржинальный доход будет содержать и прибыль, и часть постоянных затрат. Соотношение это зависит от числа изделий, произведенных до и после точки безубыточности, и с каждым новым изделием будет изменяться.

Выше мы вывели формулу для определения точки безубыточности при производстве одного продукта. Когда производится несколько продуктов, точку безубыточности тоже можно определить, только она, естественно, не будет иметь натурального выражения (штук, метров, тонн). В данном случае точка безубыточности — это минимальный объем выручки от продаваемой продукции, при которой предприятие начинает получать прибыль.

Получить достаточно простую формулу для точки безубыточности в данном случае можно только в предположении, что при незначительных изменениях объемов производства структура выручки не меняется, т. е. что на рассматриваемом интервале производство всех видов продукции повышается и понижается одинаково.

Обозначим в дополнение к уже введенным обозначениям точку безубыточности в стоимостном выражении T_min, а переменные затраты С_пер. Как известно, в точке безубыточности выручка в точности равна затратам предприятия, маржинальный доход равен постоянным затратам, т. е.

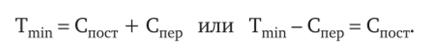
Поскольку мы считаем размер переменных затрат в расчете на единицу продукции постоянной величиной (мы рассматриваем такой интервал изменения объемов предприятия, на котором это условие выполняется), то в случае если не меняется структура производимой продукции, постоянна будет и доля переменных затрат в выручке от ее реализации.

Пусть Д — доля переменных затрат в выручке от реализации продукции. Тогда можно записать.

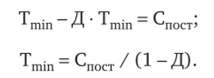
Величина (1 — Д) называется коэффициентом маржинального дохода и показывает, какую долю в объеме продаж можно использовать для покрытия постоянных издержек и формирования прибыли. Отметим, что этой формулой можно пользоваться и в случае одного продукта для получения точки безубыточности в стоимостном выражении.

С точкой безубыточности связан важный индикатор безопасности предприятия — запас финансовой прочности, который характеризует, на сколько процентов объем продаж превышает точку безубыточности. Если обозначить его ЗФП, то приведенное выше определение можно представить в виде следующей формулы:

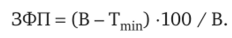
Если запас финансовой прочности предприятия равен, например, 20%, то это означает, что объемы его продаж могут уменьшиться на 20% прежде, чем будет достигнута точка безубыточности.

Запас финансовой прочности в значительной мере диктует поведение предприятия. Если оно имеет достаточный запас финансовой прочности, то значительные средства может отвлекать на разработку и обновление продукции, инвестировать средства в расширение производства, приобретать ценные бумаги.

Если предприятие имеет небольшой запас финансовой прочности, то его стратегия будет заключаться в жестком контроле за затратами и оптимизацией всей деятельности. Для такого предприятия нежелательно заниматься инвестиционными проектами, но если это необходимо, нужно тщательно оценивать их последствия с точки зрения окупаемости, так как инвестиции на первых порах — это дополнительные затраты, которые приведут к тому, что предприятие, скорее всего, вынуждено будет опуститься ниже точки безубыточности. И оно должно быть в состоянии продержаться на этом уровне, пока инвестиции не начнут давать отдачу.

Показатели, основанные на маржинальном доходе, являются мощными инструментами анализа и совершенствования производственной и коммерческой деятельности предприятия. Некоторые из этих возможностей мы рассмотрим далее.

Ранее мы видели, что при росте и снижении производства прибыль растет или снижается значительно быстрее, чем изменяется объем продаж. В этой связи представляет интерес количественная оценка изменения прибыли в зависимости от изменения объема реализации.

Показателем, связывающим изменение объема реализации и прибыли, является так называемый операционный рычаг.

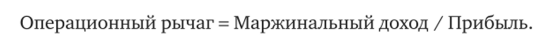
Операционный рычаг показывает, на сколько процентов изменится прибыль при изменении выручки на 1%.

Операционный рычаг характеризует уровень предпринимательского риска: чем он выше, тем выше риск. Риск здесь состоит в том, что при высоком значении рычага даже незначительное уменьшение объемов реализуемой продукции ведет к значительному падению прибыли. Например, в рассмотренной задаче операционный рычаг равнялся 4,6 (46 тыс. руб. / 10 тыс. руб.). Поэтому снижение объема продаж на 10% привело к уменьшению прибыли на 46%. Если бы значение рычага было в 2 раза больше, то при том же сокращении продаж прибыль уменьшилась бы более чем на 90%. Если бы рычаг был больше в 2,5 раза, то при таком же снижении продаж вместо прибыли был бы убыток.

Но зато большой рычаг сулит хорошие шансы в случае роста продаж. Все, что ранее было сказано о прибыли в случае уменьшения объема продаж, остается справедливым «с обратным знаком» в случае его увеличения. Однако в целом при высоком значении операционного рычага положение предприятия является не очень устойчивым, так как колебания объема продаж могут привести как к увеличению прибыли, так и к убыткам.

От чего зависит величина операционного рычага? Как следует из его формулы, при прочих равных условиях рычаг тем больше, чем больше маржинальный доход по сравнению с прибылью. Но маржинальный доход отличается от прибыли на величину постоянных затрат. Отсюда следует, что чем больше у предприятия постоянные затраты, тем при прочих равных условиях его деятельность является более рискованной, но зато и потенциально более выигрышной.

На интуитивном уровне это можно иллюстрировать следующим примером. Рассмотрим два предприятия. У одного из них заработная плата рабочих сдельная (т.е. переменная), а у другого — повременная (т.е. постоянная). Во всем остальном эти предприятия одинаковы. В случае сокращения объема продаж, например при неожиданном сокращении спроса, у первого будет сокращаться заработная плата рабочих, поэтому убытки предприятия будут относительно невелики. При увеличении объема производства будет увеличиваться заработная плата, поэтому и прибыль будет расти не очень быстро.

У второго предприятия в случае сокращения объема продаж заработная плата рабочих останется неизменной, и предприятие будет нести убытки. Но зато увеличение объема продаж не будет сопровождаться ростом заработной платы, поэтому прибыль будет расти заметно быстрее, чем у первого предприятия.

Следует иметь в виду, что из-за того, что в знаменателе формулы рычага стоит прибыль, по мере приближения к точке безубыточности размер рычага быстро растет. В этом находит отражение тот факт, что вблизи точки безубыточности риск существенно выше, чем на значительном расстоянии от нее.

Вернемся еще раз к показателю, который мы назвали коэффициент маржинального дохода и который определили как (1 — Д), где Д — доля переменных затрат в выручке от реализации продукции.

Пусть В — выручка от реализации. Тогда справедливо.

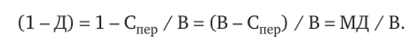
Таким образом, мы видим, что коэффициент маржинального дохода есть отношение маржинального дохода к выручке от продаж. Иными словами, это аналог рентабельности продаж, только вместо прибыли от реализации используется маржинальный доход. Поэтому и показывает он то же самое: сколько копеек маржинального дохода содержится в каждом рубле, вырученном от реализации продукции.

• [1] Здесь и далее мы рассматриваем такой интервал изменений объемов производства, при котором постоянные затраты остаются постоянными, не меняется цена продукции, а также переменные затраты в расчете на единицу продукции. Понятно, что О