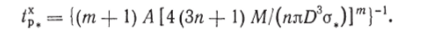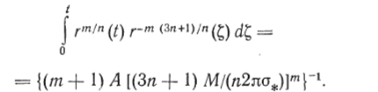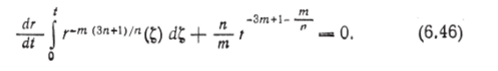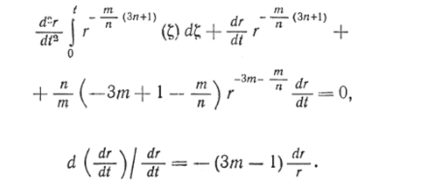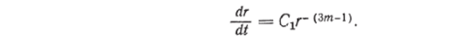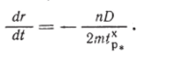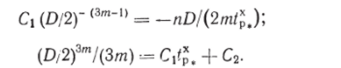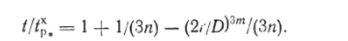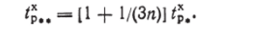Хрупкое разрушение скрученного стержня

Обозначим крутящий момент через М, диаметр поперечного сечения через D. Поскольку напряженное состояние всех точек скрученного стержня — чистый сдвиг, когда а_шах = т_п]ах, под* ставим в формулу (6.33) вместо а_гаах касательное напряжение по формулам (4.36), (4.34) при г = D!2. Тогда получим время скрытого разрушения.

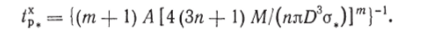
После начала разрушения в точках, наиболее удаленных от центра, оно распространяется к центру, и в некоторый момент времени разрушенной областью является кольцо, внутренний и наружный радиусы которого, соответственно г* и DI2. Фронт разрушения, который представляет собой поверхность кругового цилиндра радиусом г*, будет двигаться к центру стержня. Полное разрушение стержня имеет место при г* = 0. Уравнение движения фронта может быть получено из соотношения (6.33) подстановкой в него вместо а_шах величины т по формулам (4.36), (4.34). При этом необходимо учесть, что напряжение в точках фронта разрушения в момент времени? определяется расстоянием этих точек до центра г (t), а обобщенный полярный момент инерции определяется радиусом г (?). Тогда.

Продифференцируем это соотношение по t, которое является и верхним пределом и параметром интеграла:

Полагая в этом выражении г = D/2, получаем производную при t = t^x

¹ *р*.

Продифференцировав соотношение (6.46) еще раз, получаем откуда.

Интегрируя полученный результат, устанавливаем.

Проинтегрируем это уравнение еще раз:

Для определения постоянных С, и С₂ используем начальные условия: при t = г = D/2,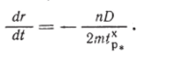

В результате получаем два уравнения:

Решая их, находим.

Подставив полученные значения постоянных в уравнение (6.47), устанавливаем зависимость времени от радиуса фронта разрушения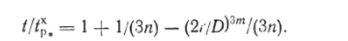

Время полного хрупкого разрушения определяется из условия равенства нулю радиуса неразрушенной части сечения г:

Поскольку величина п обычно значительно больше единицы, в рассматриваемом случае стадия распространения разрушения по времени намного меньше стадии скрытого разрушения.