Второе начало термодинамики и энтропия

Второй закон термодинамики более труден для понимания, чем первый, во-первых, из-за следующих из него важных философских выводов и, во-вторых, он требует более строгого определения границ системы. Он, так же как и первое начало, является обобщением данных опыта, и его открытие связано с анализом работы тепловых машин (сначала С. Карно, а позднее Р. Клаузиусом и В. Томсоном). Изучение закономерностей превращения теплоты в работу и работы в теплоту привело к открытию у всякой равновесной системы еще одной функции состояния — энтропии, которая, в отличие от внутренней энергии, не изменяется у изолированной системы при равновесных процессах и всегда возрастает при неравновесных.

В разделе 2.1 уже упоминалось, что два способа передачи энергии (в виде теплоты и работы) неравноценны. Если работа W может непосредственно идти на увеличение любого вида энергии, то сообщение системе количества теплоты Q, без предварительного превращения ее в работу, приводит лишь к увеличению внутренней энергии системы. При этом при превращении работы в теплоту изменяется термодинамическое состояние одного лишь теплополучающего тела, а при преобразовании теплоты в работу наряду с охлаждением теплоотдающего тела происходит изменение термодинамического состояния других тел, участвующих в этом процессе. Изменение состояния рабочего тела при незамкнутом процессе или отдача части тепла рабочим телом другим телам и изменение их термодинамического состояния при циклическом процессе называется компенсациейОпыты показывают, что без компенсации преобразовать теплоту в работу невозможно. Работа же в теплоту превращается полностью без всякой компенсации.

Отсюда следует, что если при циклическом процессе происходит преобразование теплоты в работу с отдачей положительного количества ' Циклическим процессом называется любое изменение параметров системы, в результате которого система возвращается в исходное состояние — к начальным значениям своих параметров.

тепла Q и совершенной положительной работой W, то всегда Q>W Если же работа W превращается в теплоту Q, то Ws=Q. Эти два независим ых утверждения

представляют одну из формулировок второго начала термодинамики. При этом первое утверждение в случае равновесных систем устанавливает существование энтропии и термодинамической температуры. Совместно же они описывают односторонний характер изменения энтропии при естественных процессах в замкнутых системах^[1][2]

Согласно второму началу, процессы в природе, при которых превращение теплоты в работу связано с компенсацией, могут происходить, а аналогичные процессы, не сопровождающиеся компенсацией, нс могут. Эго обуславливает разделение всех возможных в замкнутой системе процессов на обратимые и необратимые. Процесс перехода системы из одного состояния в другое называется обратимым, если возвращение этой системы из конечного состояния в исходное можно осуществить без каких бы, то ни было изменений во внешней среде. Все процессы, не удовлетворяющие этому условию, называются необратимыми.

Всякий равновесный процесс является обратимым, так как при этом процессе состояние системы в любое время полностью определяется внешним параметрами и температурой, и поэтому, при изменениях этих параметров в обратном порядке система также придет в начальное состояние, не вызвав никакого изменения во внешней среде. Обратимые процессы в реальном океане крайне редки. К ним могут быть отнесены:

• • медленное адиабатическое обтекание некоторым объемом воды возвышенности на дне при сохранении потенциальной температуры (определение будет дано позднее) и солености в начальной и конечной точках;
• • распространение волн в толще воды при отсутствии их поглощения.

Примерами необратимых процессов могут служить процессы с трением, теплопроводность за счет разности температур, передача энергии посредством излучения. В этих процессах при переходе системы в конечное состояние работа может быть превращена в теплоту без компенсации, а в обратном направлении переход системы связан с переходом теплоты в работу, что невозможно осуществить без изменения во внешней среде. Отметим, что всякий необратимый процесс является неравновесным.

Остановимся теперь на физическом смысле энтропии. Согласно первому началу термодинамики, элементарная теплота 8Q не является полным дифференциалом, т. е. количество теплоты, необходимое при переходе из начального состояния в конечное, зависит от условий перехода (от пути). Пусть этот переход может быть осуществлен по пути I или II. Тогда количество теплоты, затраченное при переходе из состояния 1 в 2, соответственно равно.

причем в соответствии с первым началом Qj ф Од. Но если количество теплоты разделить на температуру Т, то, в соответствии с многочисленными опытами, интегралы приведенных те плот для обоих путей перехода будут одинаковы:

Выявленная независимость от пути означает, что величина 8Q/T должна быть полным дифференциалом некоторой величины, представляющей собой функцию состояния системы.

Функция состояния (термодинамический параметр) ц, полный дифференциал которой равен.

называется энтропией (от греческого слова entropia — поворот, превращение). Впервые это понятие ввел в термодинамику Р. Клаузиус (рис. 2.4.1), причем он обозначил энтропию через S. Однако, учитывая, что в океанологии этот символ означает соленость, мы для обозначения энтропии выбрали т|. Важно отметить, что значение 5Q сопоставляется с температурой Т системы в целом.

На основе многовековых опытов установлено, что в любой изолированной системе процессы выравнивания температуры, давления и концентрации, а также процессы преобразования кинетической, потенциальной, электрической, химической и ядсрной энергии во внутреннюю приводят к возрастанию энтропии системы. Иначе говоря, любой спонтанный (самопроизвольный) процесс в любой изолированной системе всегда приводит к росту энтропии этой системы (одна из формулировок второго начала)^[3]. Если увеличение энтропии в некоторой системе невозможно, то в такой системе нс может происходить никаких самопроизвольных изменений. Энтропию системы можно уменьшить в результате соответствующего обмена теплом с окружающей средой, в то же время путем совершения работы это осуществить невозможно. В общем случае энтропия системы может производиться внутри системы за счет необратимых процессов или поступать в систему в результате теплового взаимодействия с внешними телами. Энтропия может переходить от системы к внешним телам или наоборот, но ее количество никогда не уменьшается. Отметим, что для равновесных циклических процессов выполняется равенство Клаузиуса.

Рис. 2.4.1. Клаузиус Рудольф Юлиус Эмануэль (1822−1888) Немецкий физик, один из основателей термодинамики. Ввел понятие энтропии

Анализ процессов, происходящих в изолированных системах, показывает, что отмеченное ранее возрастание энтропии, сопровождающее превращение различных форм энергии во внутреннюю, следует рассматривать как необратимую потерю способности системы к совершению работы [Фен, 1986]. Так, например, в процессе выравнивания концентрации растворенной в воде соли могла бы совершаться работа. Однако в изолированной системе при свободной диффузии не совершается никакой работы, так что соответствующий потенциальный запас работы теряется навсегда.

Более глубокий смысл энтропии основан на рассмотрении молекулярной структуры системы. Из статистической физики известно, что энтропия системы в данном состоянии характеризует вероятность этого состояния:

где к — постоянная Больцмана; Р — термодинамическая вероятность состояния, определяемая соответствующим числом микрососшяний. Возрастание энтропии в результате спонтанного процесса соответствует.

Рис. 2.4.2. Больцман Людвиг (1844−1906)

Австрийский физик, один из основателей статистической физики

переходу из состояния с меньшей вероятностью в состояние с более высокой вероятностью. С этим связано представление о том, что энтропия возрастает по мере увеличения степени беспорядка (хаоса) в системе. Л. Больцман (рис. 2.4.2) первым установил соотношение (2.4.5). Эта формула выгравирована на кладбище в Вене на его памятнике¹.

Обобщая все вышесказанное, можно видеть, что второе начало термодинамики определяет существование энтропии у всякой равновесной системы и ее неубывание при любых процессах в изолированных и адиабатических изолированных системах [Базаров, 1991].

Подставив (2.4.3) в уравнение первого начала термодинамики.

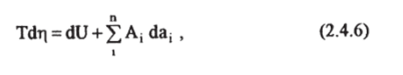
• 1 Отметим, что термодинамическую вероятность Больцман обозначал буквой W, а не Р.
• (2.3.1) с учетом (2.1.1), получим основное уравнение термодинамики для равновесных процессов выраженное исключительно через параметры системы. Все дифференциалы, входящие в (2.4.6), являются полными.

Для простой системы, находящейся под всесторонним (одинаковым в каждой точке внешней границы) давлением р, уравнение (2.4.6) с учетом (2.1.2) примет вид.

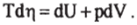
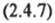
Энтропия тела может быть вычислена только с точностью до постоянного слагаемого:

где интегрирование производится вдоль произвольного обратимого процесса, a rjo — значение энтропии тела при Т=0°К, которое не может быть определено с помощью первого и второго законов термодинамики.

• [1] ‘Стрелка указывает на направление протекающег о процесса.
• [2] Под односторонностью естественных процессов подразумевается исчезновениепотенциально возможной работы при самопроизвольных процессах взамкнутых системах.
• [3] В открытой системе при соответствующих условиях может происходить ипонижение энтропии.