Общая степенная и тригонометрические функции. 
Функция Жуковского

Пример 12.1. Найти все значения функции w = z^l в точке 2 = г. Решение. Поскольку Lnt = lnl-M^ + 2тгkj, то.

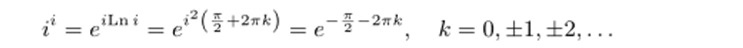
В данном случае все искомые значения функции оказались действительными.

При ft = О получаем.

Отсюда следует, что значения степенной функции отличаются лишь аргументами Ок = о (у? + 2т: к). Если а — рациональное число, т. е. оно пред;

TYI

ставимо несократимой дробью а = — (га и п целые числа), то среди в к

п

имеется лишь п значений, определяющих различные значения z^a:

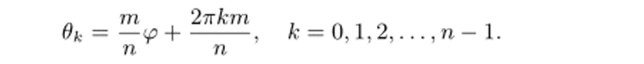
При к = п, п+1,… мы получим значения Ок, отличающиеся от уже известных на числа, кратные 2тг. Значит, для таких значений к мы не получим новых точек z^a. Итак, при а = m/п формула (12.1) дает (мы пользуемся также равенством е^а 1пг = г^а для действительных чисел г, а):

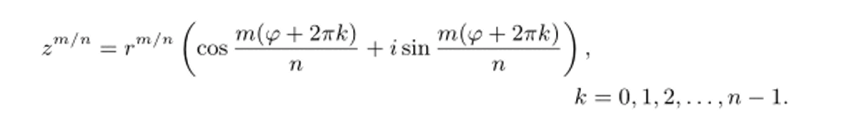
Сравнивая эту формулу с (2.12) мы видим, что.

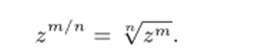
Таким образом, для рациональных показателей а функция z^a является конечнозначной. При иррациональных (действительных) а = а среди значений аргумента Ок = а (у? + 27гАт) нет чисел, отличающихся друг от друга на величины, кратные 2тг. (Если бы нашлись такие натуральные числа к 1, к'2,1, что 0к₂ — Okj = 2тт/, т. е. 2ттк2<�х — 2т: к (х = 2т:I и к ф к2, то 1.

q = —— и, следовательно, а — рациональное число, что противоречит л*2 — к 1.

сделанному предположению.) Поэтому для иррациональных показателей а функция z^a бесконечнозначна. Ее риманова поверхность такая же, как и риманова поверхность логарифма.

Общая степенная функция w = z^a в сил}' своего определения допускает выделение регулярных ветвей в тех же областях, что и логарифмическая; например, в плоскости с разрезом по лучу. Ветвь.

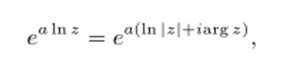
выделенная в плоскости с разрезом вдоль отрицательной полуоси, называется главной ветвью степенной функции. Если z^a+b, z^a, z^b — регулярные ветви степенной функции, выделенные с помощью одной и той же ветви логарифма, то справедливы равенства.

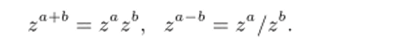
Действительно, пусть f (z) регулярная ветвь логарифмической функции Ln z. Выведем первое равенство (второе выводится аналогично):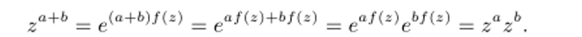

Применяя теорему о производной сложной функции, равенства f'(z) = ½, z = e^^z а также свойства показательной функции, для каждой регулярной ветви степенной функции получаем:

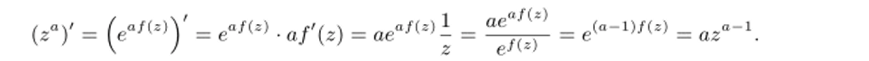
Мы вывели обычную формулу для производной степенной функции:

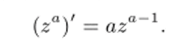
2. Перейдем к тригонометрическим функциям. Для действительных значений х из формулы Эйлера (2.14) следует, что.

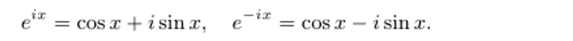
_eix _е-хх _eix _ _e-ix.

Отсюда cos л; =—-, sin х = -—-. Эти формулы служат осно;

вой следующего определения.

Тригонометрические функции комплексного переменного z определяются равенствами.

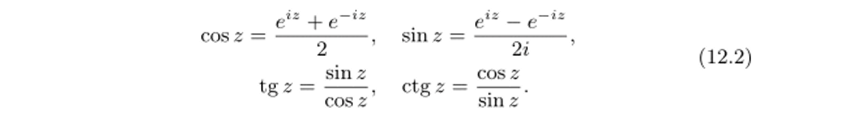
Определенные таким образом функции сохраняют многие свойства тригонометрических функций действительного переменного. Из периодичности функции e^z следует, что функции sin 2 и cos 2 периодичны с периодом 2п, a tg2 и ctg 2 — с периодом тг. Функция sin 2 нечетна, a cos 2 — четна. Действительно,.

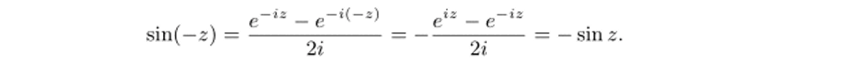
Аналогично доказывается четность функции cos 2 (докажите!). Для функций, определенных равенствами (12.2), справедливы обычные тригонометрические соотношения. В частности,.

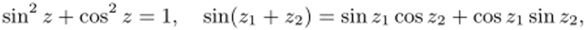
и т.д. Все эти соотношения вытекают из (12.2). Докажем, например, Функции sin г и cos z аналитичны во всей плоскости С, причем имеют место обычные формулы дифференцирования:

iгоследн юю формулу:

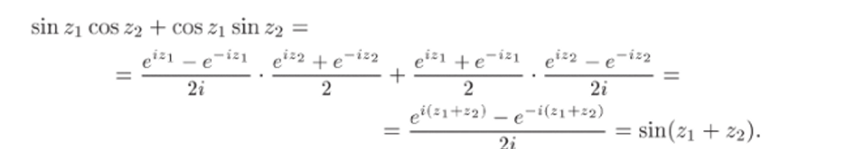
Докажем, например, формулу для производной sin г:

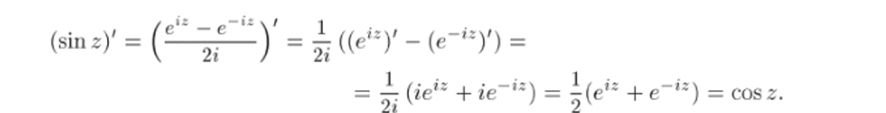
Используя формулы для производной частного, получим.

Однако не все свойства тригонометрических функций действительного переменного сохраняются при продолжении этих функций в комплексную плоскость. В частности, sin 2 и cos 2 могут принимать значения, по модулю превосходящие 1. Например,.

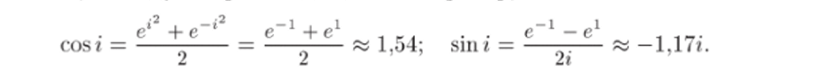
3. Функции, обратные (12.2), называются обратными тригонометрическими функциями. Так как тригонометрические функции (12.2) периодичны, то обратные к ним функции будут бссконечнозначными. В силу того что функции (12.2) достаточно просто выражаются через показательные, обратные к ним функции удается выразить через логарифмы. Получим такое выражение, например, для w = Arccosz. Из определения этой функции имеем.

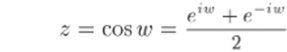
откуда e^2tw — 2ze^tw + 1 = 0. Решая это квадратное уравнение относительно e^iwу находим e^lw = z + y/z² — 1 (мы опускаем ± перед знаком квадратного корня, поскольку понимаем корень как двузначную функцию, принимающую оба соответствующих значения). Из последнего равенства получаем.

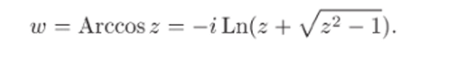
В силу соотношения (z + y/z'² — 1)(г — yjz² — 1) = 1 изменение знака перед корнем приводит к изменению знака перед логарифмом. Но корень принимает значения как с «+» так и с «. Значит, и среди значений Arccos2 будут значения как с так и с «перед логарифмом. Поэтому знак «можно не писать:

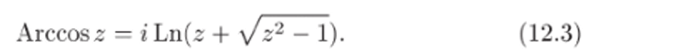
Аналогичные формулы можно дать и для других обратных тригонометрических функций:

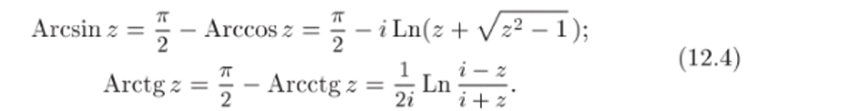
Из элементарных функций комплексного переменного отметим также гиперболические функции shz, eh*, th-г, и cth-г, определяемые равенствами.

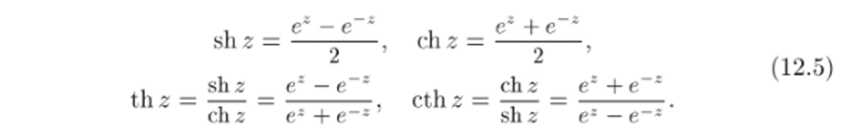
Они весьма просто выражаются через тригонометрические функции:

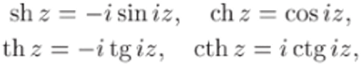
и поэтому несущественно отличаются от последних.

Пример 12.2. Найти Arcsin 2.

Р е ш е н и е. По формуле (12.4).

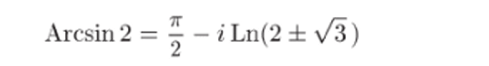
(мы поставили «±» перед корнем, поскольку /3 обычно понимается как арифметическое значение корня). Для вычисления логарифма используем формулу (11.5), в которой полагаем z = 2 ± /3, arg г = 0. Получаем.

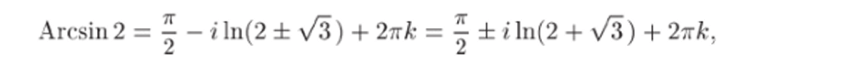
где Д — арифметическое значение корня и к — любое целое число. 4. Функцией Жуковского называется функция.

Эта функция имеет важные применения в теории крыла самолета, а также весьма полезна при построении ряда конформных отображений. Она аналитична всюду' в С, кроме точек z = 0 и z = оо. Производная.

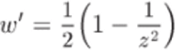
существует всюду' в С, за исключением точек 2 = 0иг = оо, и обращается в нуль при z = ±1. Поэтому отображение (12.6) конформно всюду, кроме точек 0, ±1 и оо¹.

Выясним, при каком условии две различные точки переходят в одну и ту же точку. Пусть z ф z^ и.

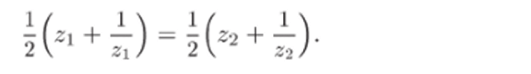
Отсюда следует, что.

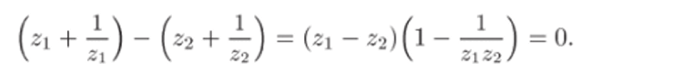
Так как z ф zo, то это равенство равносильно условию.

Поэтому для однолистности функции Жуковского в некоторой области D необходимо и достаточно, чтобы эта область не содержала пары различных точек, удовлетворяющих условию (12.7). Такими областями являются, например, внешность z > 1 единичного круга (при этом z2 > 1) и внутренность z < 1 этого круга (|2i2fe| < 1);

Чтобы наглядно представить себе отображение (12.6), выясним, в какие кривые оно переводит окружности (показаны на рис. 27, а сплошными линиями) и лучи (показаны пунктирами). Положим г = = Тогда (12.6) перепишется в виде.

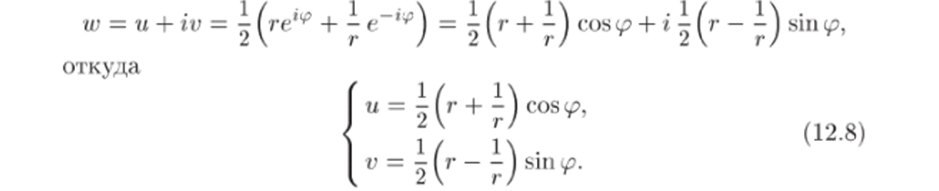
Рассмотрим образы окружностей г = 7*о. Из (12.8) следует.

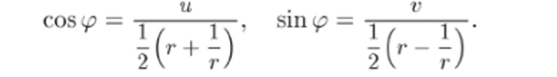
¹ Используя определение угла в бесконечно удаленной точке можно показать, что отображение (12.6) конформно и в точках 0 и оо. В точках ±1 оно конформным не является.

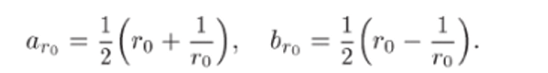
Итак, образами окружностей z = го в плоскости 2 будут эллипсы в плоскости w (рис. 27, б). Если г₀ —> 1, то а_го —> 1, Ь_Го —> 0. Поэтому эллипсы будут стягиваться к отрезку [—1.1]. При больших го раз- ', 1.

ность п_Го — о_Го = — мала, и эллипсы мало отличаются от окружного стой.

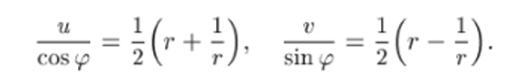
Возводя эти равенства в квадрат, вычитая из первого второе и полагая 9 = 9о, получим.

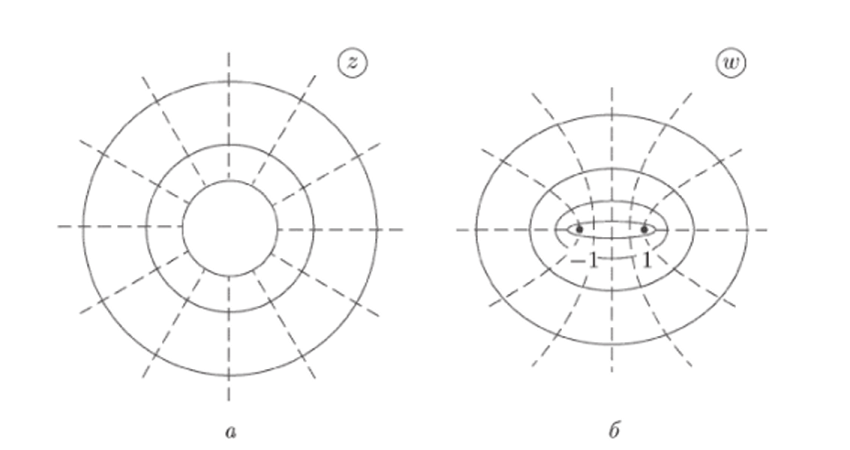
Рис. 27.

Возводя эти равенства в квадрат, складывая и полагая г = 7*о, получим.

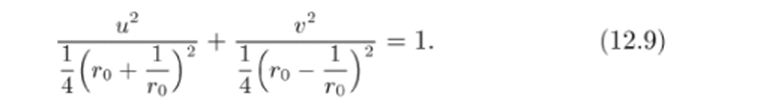
Уравнение (12.9) является уравнением эллипса с полуосями Чтобы получить образ лучей 9 = 90, преобразуем равенства (12.8) к виду.

Уравнение (12.10) является уравнением гиперболы с полуосями о^₀ = = |cos9o|, by о = | sin 901 — Следовательно, лучи 9 = 90 отображаются в части гипербол (рис. 27, б).

Таким образом, функция Жуковского взаимно-однозначно и конформно отображает внешность единичного круга на внешность отрезка [-1,1].

Из (12.6) легко видеть, что w (z) = w (l/z). Функция w = 1/z взаимно-однозначно и конформно отображает внутренность круга z < 1 на внешность этого же круга. Отсюда следует, что функция Жуковского взаимно-однозначно и конформно отображает также и внутренность единичною круга на внешность отрезка [—1,1].