Морфометрические параметры и показатели водоёмов

Важнейшим, базовым разделом лимнологии считается морфометрия водоёмов. Морфометрией в лимнологии называется совокупность методов количественного выражения размеров и формы водоёмов. Как и в морфометрии речных водосборов, основой определения всех морфометрических характеристик озёр и водохранилищ служат крупномасштабная карта или план в изобатах (рис. 2.4). На плане озера, в отличие от карты, нет географических координат и высоты над уровнем моря. Изобата — это линия, соединяющая точки одинаковой глубины, которая оконтуривает его чашу на горизонтальной поверхности, секущей объем воды на той или иной глубине. Поэтому расстояние по вертикали между этими поверхностями называется сечением изобат. На рис. 2.4 сечение изобат равно 2 м, при этом обычно говорят: «Изобаты проведены через 2 м». Нулевая изобата называется урез.

На каждом таком плане обязательно имеется масштаб, необходимый для выполнения картометрических работ. Степень детальности изображения подводного рельефа озёрной чаши зависит от методики промерных работ, которая выполняется по промерным галсам: обычно — по поперечным, продольным разрезам или их какой-либо сетке. Методическими работами на шведских озёрах показано, что при сгущении эхолотных профилей вдвое погрешность оценки вслиРис. 2.4. План озера в изобатах (а): I — остров.

чины площади озёрной чаши внутри изобаты, а следовательно и погрешность вычисления объема воды в озере, снижается с 19% до 9%.

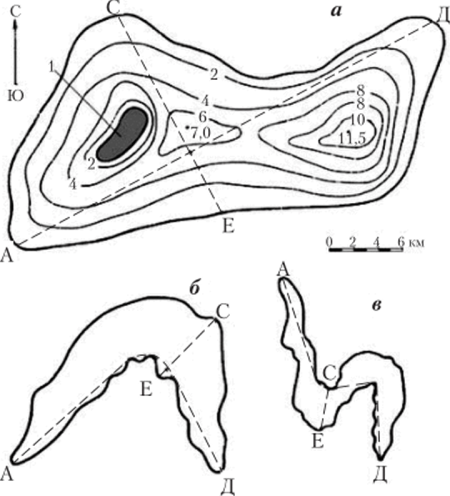
На планах озёр изогнутой формы (б) и (в) продольная ось А-Д показана ломанными линиями Кроме того, точность промерных работ зависит не только от частоты измерений глубины (в настоящее время используются эхолоты с практически непрерывной записью глубины по промерным разрезам), но и от точности измерительных приборов — эхолотов и спутниковой системы географического позиционирования (GPS), которые все время совершенствуются.

Для примера: максимальная глубина Байкала, измеренная в 1931 г. Г. Ю. Верещагиным и Б. Н. Форшем со льда^[1][2] с помощью большого груза на металлической проволоке, составила 1741 м. Детальными же эхолотными промерами озера в конце XX века удалось обнаружить наибольшую из глубин, равную лишь 1636 м (завышение глубины, измеренной специальным лотом, могло быть связано с его отклонением от вертикали).

Очень важно при выполнении морфометрических работ указывать:

• 1) масштаб карты водоёма или плана, который характеризует степень детальности изображения рельефа дна;
• 2) абсолютную или относительную высотную отметку уреза в период промерных работ. В этом состоит важное отличие лимнологических работ от топографических съёмок. Ведь водоёмы имеют вогнутую форму чаши или ложа, поэтому все их морфометрические характеристики существенно изменяются в зависимости от того уровня воды, при котором проводились промеры. Поэтому судить об изменении размера и формы водоёма от одной его батиметрической съёмки к другой возможно лишь с учётом разности уровней в дни промерных работ. От соблюдения эти двух батиметрических правил зависит степень достоверности результатов, полученных при изучении истории развития ложа водоёма и его экосистемы, при оценке его водных и биологических ресурсов.

Непременное требование к морфометрическим работам состоит еще и в том, что метод определения на карте или плане каждой морфометрической характеристики водоёма должен быть стандартизирован и общепринятым. Измерять ту или иную характеристику следует так, чтобы любой другой исследователь, начинающий такие измерения по новой карте в другой момент жизни озера, получал результаты, сопоставимые с предшествующими измерениями.

Значимости морфометрической стандартизации в лимнологии посвящена опубликованная в 1948 г. крупная статья С. Д. Муравейского «Очерки по теории и методам морфометрии» (Муравейский, 1960), в которой им выполнен критический анализ более 120 научных работ географов, геоморфологов, гидрологов и лимнологов.

Морфометрические характеристики водоёма подразделяются на параметры, т. с. его абсолютные размеры, и показатели его формы.

Параметры водоёма:

• 1) длина береговой линии /о, т. е. длина нулевой изобаты, или уреза воды;
• 2) площадь акватории F. Если озеро имеет острова, то площадь водной поверхности

где Х^о-в — суммарная величина площади островов;

• 3) длина водоёма L- это кратчайшее расстояние между двумя наиболее удаленными друг от друга точками береговой линии, измеренное по его водной поверхности. На рис. 2.4 видно, что в озёрах и водохранилищах разной формы и извилистости длина измеряется по прямой или ломаной линии А-Д с перегибом на урезе вдающегося в акваторию берега (полуострова);
• 4) максимальная ширина #_макс — наибольшая длина линии, перпендикулярной к линии измеренной длины. Поэтому нужно, выставляя перпендикуляры в разных частях плана акватории водоёма, пересекающие его от одного берега до другого, найти из многих вариантов тот, который составит наибольшую длину поперечного разреза С-Е на рис. 2.4, перпендикулярного на плане линии А-Д, по которой измерена длина водоёма;
• 5) наибольшая глубина Я_макс— снимается с карты или плана. Если на карте не указана точка максимальной глубины, значит, дно плоское (в пределах точности измерения глубины), и за величину Я_макс принимается глубина самой нижней изобаты;
• 6) площадь дна озера F_}X рассчитывается по формуле

где, а — средний угол наклона дна, который определяется по тангенсу этого угла.

где h — сечение изобат, ?/ - сумма длин всех изобат, F₀ — площадь водной поверхности водоёма. При, а 0,9, поэтому можно принимать.

• 7) объём водоёма W, методика вычисление которого изложена ниже в разделе 2.4;
• 8) глубина инерционного центра водоёма Ню Её определение — в разделе 2.4.

Показатели формы водоёма:

1)средняя глубина

Этот показатель особенно часто используется для сравнения форм озёрных чаш. Среднюю глубину водоёма можно представить и как среднюю арифметическую величину бесконечного множества измеренных глубин, и как среднее геометрическое значение высоты цилиндра, равновеликого по объёму и площади данному озеру, но в то же время — это удельный объём, т. е. в среднем объём воды который находится под 1 м² водной поверхности. Такая трактовка показателя Я_ср — уже нс математическая, а экологическая: чем меньше Я_ср, гем большую долю объёма водоёма составляет фотический слой воды, освещенный днём солнечным светом, тем благоприятнее световые условия для биологической продуктивности водной экосистемы. Одновременно Я_ср— это средний объём воды и над 1 м" батиали. И поэтому при одинаковой насыщенности взвешенными веществами воды в двух водоёмах из-за различия этого показателя в них будет разная скорость илонакопления, необходимого для питания бентоса. Поэтому значение Я_ср часто используется лимнологами для сравнения экологических условий жизнедеятельности в них биоты, её продуктивности. Статистический анализ морфометрических показателей озёр мира показал, что среди них наибольшим разнообразием величины Я_ср (от сантиметров до сотен метров) отличаются небольшие озера площадью в несколько десятков квадратных километров;

2) средняя ширина.

Так она вычисляется для озёр и морфологически простых долинных водохранилищ. Но если это соотношение площади и длины водоёма использовать для многолопастных водохранилищ, то не исключены случаи, когда средняя ширина такого водоёма получится больше максимальной ширины.

Например, Вазузскос водохранилище (рис. 2.5) с тремя протяженными и узкими плёсами по долинам притоков Касня, Гжать и Осуга имеет площадь при НГ1У 106 км², длина по главной Вазузской долине — более 77 км. При максимальной ширине в приплотинном участке 0,7 км, но равенству (2.6) получим парадоксальное значение В= 1,4 км.

Рис. 2.5. Морфолошчески сложное четырёхлопастнос Вазузское водохранилище с Зубцовским гидроузлом (ЗГУ). Лопасти: Вазузская (У), Осугская (2), Гжатская (3) и Каснснская (4); Н21 — насосная станция перекачки воды в канал (5) для переброски резервных водных ресурсов в Москворецкую водохозяйственную систему.

Поэтому для вычисления средней ширины морфологически сложных водохранилищ с коэффициентом разветвленности у >1,5 (см. формулу 2.1) следует использовать морфоло;

гически обоснованную формулу.

где Lo - длина главной долины, YJL, — суммарная длина затопленных участков долин притоков. Рассчитанное по ней для Вазузского водохранилища реальное значение В_кр = 0,6 км. Средняя ширина различных водоёмов используется для их сравнения по роли ветроволновой активности на их акваториях, определяющей интенсивность гидродинамических процессов в штормовую погоду, их воздействие на переработку берегов вновь созданных водохранилищ и вертикальное распределение планктонных организмов;

3) удлиненность водоема Минимальное значение удлинённости дли абсолютно круглой или квадратной формы равно 1 (L = В). Чем сильнее вытянут водоём, тем неравномерней ветровое воздействие на динамические процессы в нем при различных направлениях ветра, что определяет специфику сейшевых и сгонно-нагонных явлений, дрейф с перераспределением планктона от подветренного берега к наветренному,;

4) относительная глубоководность.

Эта характеристика введена в лимнологию Д. Хатчинсоном. Ее рекомендуется использовать для сравнения водоёмов по глубине проникновения ветроволнового перемешивания их водной толщи с целью экологических оценок неизученных стратифицированных водоёмов при их сравнении с соседними уже лимнологически изученными. Так как величина //_ср измеряется в метрах, даже для Байкала, а В_ср чаще всего в километрах, то величину х обычно выражают в промилле (%о);

6) коэффициент ёмкости характеризующий ёмкость озёрной чаши. Из двух озёр, имеющих одинаковую площадь акватории и максимальную глубину, объём водной массы больше в том водоёме, у которого больше коэффициент ёмкости.

8) коэффициент формы водоёма к_Ф = Я_ср/Я/с, Его определение — в разделе 2.5.

• [1] Hakanson L. A Manual of Lake Morphometry. — N.-Y.: Springcr-Vcrlag, 1981. — 78 p.
• [2] Фортунатов M. А. Верещагин Г. Ю. — исследователь Байкальского озера и его рольв развитии нового направления в лимнологии // Деятели советской лимнологии. -М.-Л.: Изд-во АН СССР, 1963. — С. 50−75.