Резонансные цепи. 
Общая теория связи

Выделение полезного сигнала из смеси побочных сигналов и шумов осуществляют частотно-избирательными цепями.

Последовательный колебательный контур

Последовательный колебательный (часто — резонансный) контур состоит из последовательно соединенных сопротивления R, индуктивности L и емкости С (рис. 4.11, а).

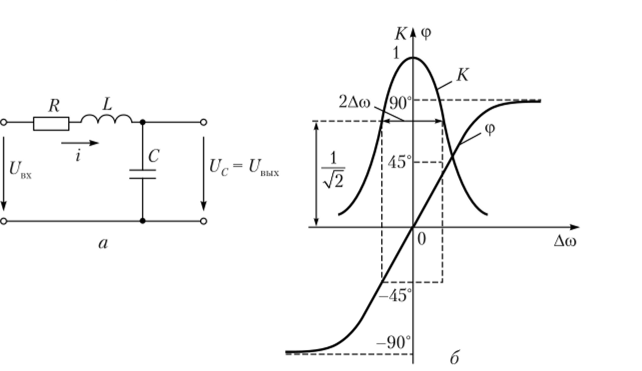
Рис. 4.11. Последовательный колебательный контур:

а — схема; 6 — ЛЧХ и ФЧХ Обычно резистор R определяет сопротивление омических потерь провода, из которого выполнена индуктивность. Сопротивление потерь емкости мало, и его на практике не учитывают. Положим, что на входе последовательного контура действует гармоническое напряжение с амплитудой U_BX и частотой со. Запишем полное входное сопротивление (импеданс — устаревшее название) контура.

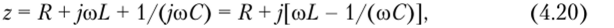
где у col и 1/(/соС) — реактивные сопротивления индуктивности и емкости.

Частоту со_р, на которой реактивная составляющая входного сопротивления равна нулю, называют резонансной. Приняв дг (со_р) = со L — 1/(со_рС) = 0, находим.

где / — циклическая резонансная частота контура.

На резонансной частоте входное сопротивление контура определяется омическими потерями и равно R. На других частотах реактивное сопротивление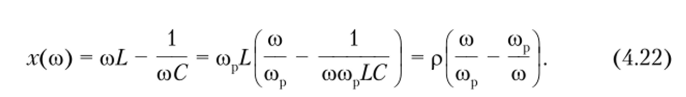

Реактивное сопротивление индуктивности или емкости на частоте резонанса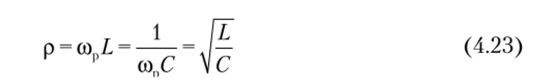

называют характеристическим сопротивлением контура.

Преобразуем полное входное сопротивление контура (4.20) к виду.

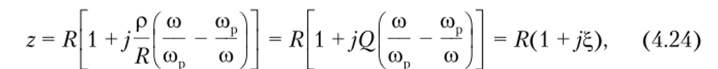
где 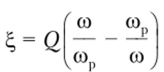 — обобщенная расстройка; Q = р/R — добротность контура.

Ток, протекающий в контуре, описывается выражением.

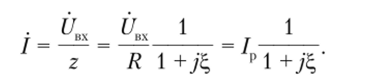
Ток в последовательном резонансном контуре, имеющий максимальное значение па частоте резонанса /_р = U_BX/R, называют резонансным током. Введем понятие частотного коэффициента передачи по току:

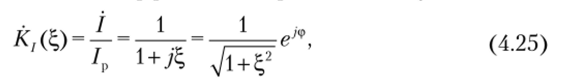
где ф — величина сдвига фазы входного сигнала на выходе контура.

При больших добротностях (Q 1; реальные значения 250—500) со ~ со_п и.

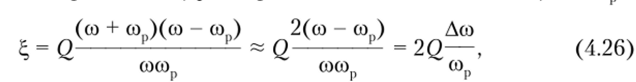
где Асо = со — со_р — абсолютная расстройка контура относительно входной частоты.

Подставив в соотношение (4.25) значение ^ из формулы (4.26), найдем модуль частотного коэффициента передачи для малой расстройки частоты:

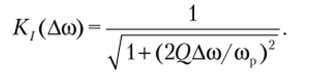
Функция Kj (Асо) отражает АЧХ контура — резонансную кривую (см. рис. 4.11, а).

Так как па границах полосы пропускания АЧХ К,(Асо) = 1/V2, то ее ширина (для колебательных контуров полосу пропускания записывают через 2Асо_р).

В выражении (4.25) аргумент функции определяется формулой ср = = arctg (2QA (o/co_p) и представляет собой ФЧХ контура для малых расстроек (см. рис. 4.11, б).

Так как на частоте резонанса напряжения на контуре U_m=I R, U_c= /_рр, то.

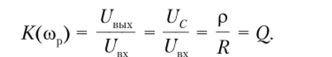
Итак, при настройке контура в резонанс амплитуда напряжения на конденсаторе (или индуктивности) в Q раз больше амплитуды входного напряжения. Поэтому резонанс в последовательном контуре называют резонансом напряжений.

Пример 4.2.

В последовательном контуре частота резонанса /₀ = 465 кГц, а добротность (2= 100. Найдем полосу пропускания контура, но циклической частоте.

Решение

Используя формулу (4.27) для циклической частоты, находим: