Порядок расчета переходных процессов операторным способом

Порядок расчета переходных процессов операторным способом следующий:

• 1) для исходной цепи составляется система уравнений, но правилам Кирхгофа, описывающая процессы, происходящие в цепи после коммутации. При этом учитываются начальные условия;
• 2) уравнения искомых функций времени, полученные в п. 1, заменяются уравнениями изображений оригиналов. Для опытного расчетчика можно сразу составить уравнения изображений, тогда п. 1 отпадает;
• 3) решают уравнения, составленные по п. 2, и получают искомые функции или величины в форме изображений;
• 4) используя теорему разложения, переходят от изображений, полученных в и. 3, к оригиналам.

Проиллюстрируем приведенный алгоритм на следующих качественных примерах.

А. Цепь, но рис. 7.9 при нулевых начальных условиях, т. е. г₁(0_) = 0 и Uc (0) = 0, подключается ключом К к постоянному напряжению U. Требуется записать изображения токов и сопротивлений, пользуясь законом Ома.

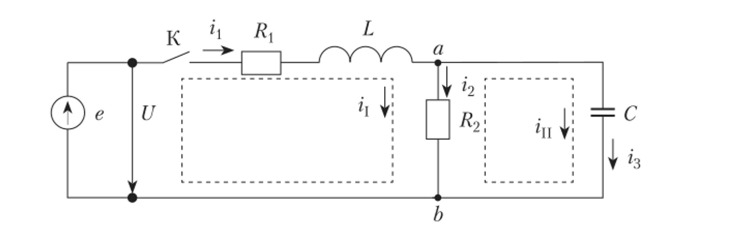
Рис. 7.9.

Запишем токи в символической форме:

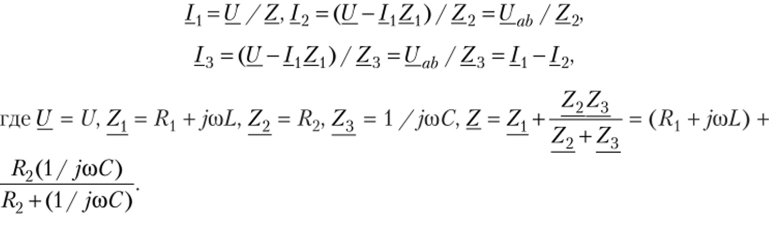
Б. Цепь на рис. 7.9 при нулевых начальных условиях подключается ключом К к переменной ЭДС е. Требуется определить токи методом контурных токов в операторной форме, если известны ЭДС и элементы цени.

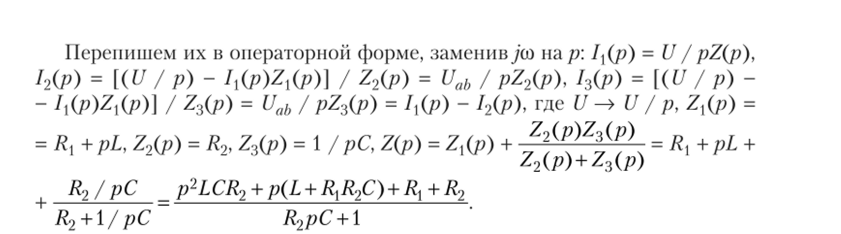
Запишем второе правило Кирхгофа для контурных токов ц и г_и, произвольно выбранные направления которых указаны на рис. 7.9:

Перепишем уравнения в изображениях:

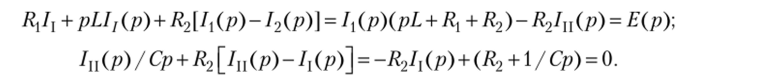
Решив полученную систему уравнений, получим.

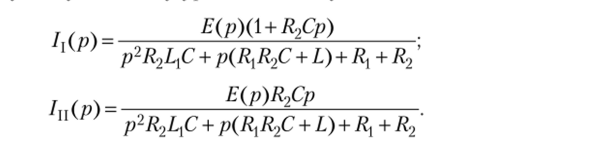
Находим изображения реальных токов в цепи:

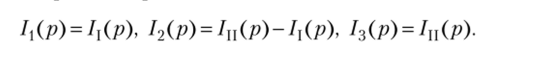
Вопросы и задания для самопроверки.

• 1. В чем заключается сущность операторного способа анализа и расчета переходных процессов в электрических цепях? Напишите формулу прямого преобразования Лапласа.
• 2. Пользуясь формулой прямого преобразования Лапласа, напишите изображения напряжений на емкости и индуктивности.
• 3. Напишите закон Ома для неразветвленной цепи с г, L, С.
• 4. Напишите правила Кирхгофа для разветвленной цепи с г, L, С.
• 5. Какова последовательность анализа и расчета переходных процессов операторным способом?
• 6. Каким образом находят оригинаны с помощью теоремы разложения?

Решенные задачи Задача 7.4. В схеме по рис. 7.10, а даны: {/=110 В, R = 20 Ом, L = 5 Гн. Определить законы изменений тока i и напряжения u_L после коммутации. Задачу решить с использованием табл. 7.1.

Рис. 7.10.

Решение

Изображения напряжения, сопротивления и тока в цепи будут: ?/(/?) = U / р =.

= m/p, Z (p)=R+pL=20₊p5=5(p₊A), I (p) = U (p)/Z (p)=~—-Ц-=5 —.

5 р{р + 4) р (р + 4).

В соответствии с табл. 7.1 оригинал тока i = 5(1 — e~^4t) А. Напряжение на индуктивности u_L = Ldi / dt=5 ? 4е~^/1' = 20е'^1t В.

Задача 7.5. В схеме по рис. 7.10, б ток источника тока нарастает по законуJ= 2,51, R = 400 Ом, С = 2500 мкФ. Определить закон изменения тока г, после коммутации, а также его величину при t = 0,5 с. Задачу решить, используя табл. 7.1.

Решение

Согласно табл. 7.1 изображение оригиналаJ = 2,5t —>J (p) = 2,5 / р². Изображение искомого тока запишется так:

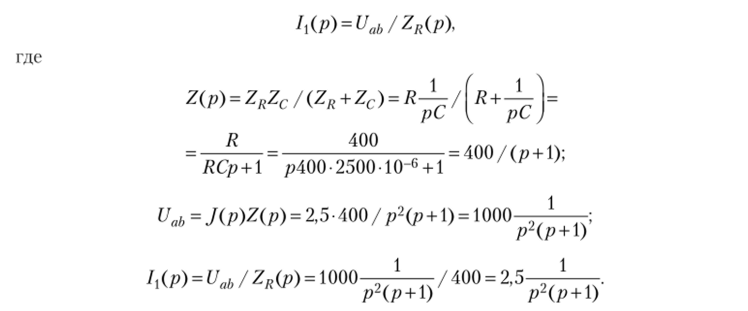
В соответствии с табл. 7.1 оригинал изображения /,(/;) будет 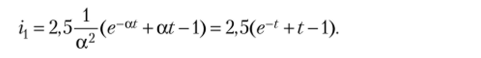При t = 0,5 с г, = 2,5(е-°.5 + 0,5 — 1) = 0,28 А.

Задача 7.6. Цепь по рис. 7.11, а при нулевых начальных условиях подключается ключом К к постоянному напряжению U. Определить законы изменения тока i₂ и напряжения на конденсаторе и_с, если известно: 11= 110 В, Л, = 50 Ом, R₂ = 60 Ом, С = 100 мкФ. Задачу решить с использованием табл. 7.1 и теоремы разложения. Решение с использованием табл. 7.1

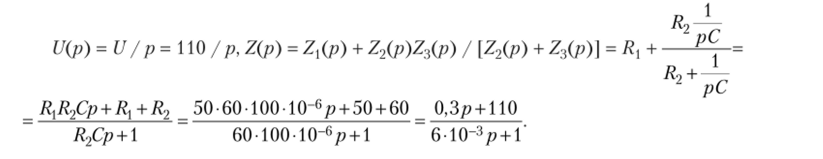
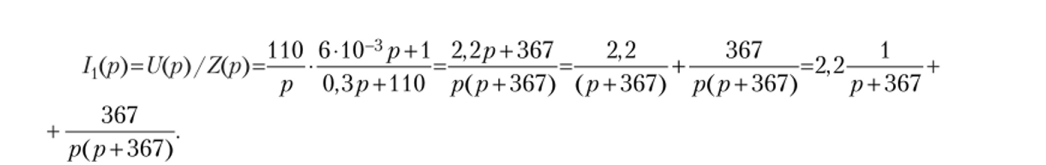
Рис. 7.11.

Законы изменения тока i и напряжения и_с во время переходного процесса в цепи по рис. 7.11, рассчитанные с использованием табл. 7.1 и теоремы разложения, совпадают, как и должно быть.

Задача 7.7. Цепь на рис. 7.11, б при нулевых начальных условиях подключается ключом К к постоянному напряжению U. Определить законы изменения тока i и напряжений на R, Lu С, если известны: U= 110 В, R = 500 Ом, 1 = 4 Гн, С =100 мкФ. Задачу решить классическим и операторным (с использованием теоремы разложения) способами.

Решение задачи классическим способом

Решение задачи классическим способом приведено в задаче 7.3. Значения искомых величин, полученных в ней, следующие: и_с = 110[ 1 + 25(e^-100r — 4e~^25t)], i = = 0,37(25'- e~^mt), u_L = 37(4100'- e~^25t), u_R = 185(25'- e~^m<).

Решение задачи операторным способом с использованием теоремы разложения Запишем изображения напряжения и сопротивления цепи: U (p) = 110 /р_у Z (p) = = R + pL +1 /рС = 500 + Ар = 1 //И 00 • 10-⁶= (4р² + 500/; + 10⁴) /р.

Найдем изображение тока:

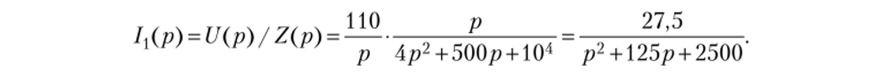
Из полученного очевидно, что F_{(p_k) = 27,5; F₂(p_k) = р² + 125р + 2500.

Найдем корни p_k из F₂(p_k) =р²+ 125р + 2500 = 0:

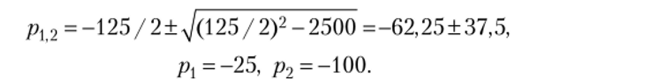
Определяем производную F₂(p_k) = 2р+ 125.

Находим: = 27,5, F_{(p₂) = 27,5; /^(Pi) = 2(-25) + 125 = 75, F₂(j)) = 2(—100) +.

+ 125 = -75.

Определяем ток в цепи: /(?) = i = ?= Ililhl + IAEll = ^1^._е-25г +.

& FiiPi) ^(ft) 75.

+^Ще~'^т = 0,37(e-^25t — e~^mt).

Находим искомые напряжения: и_к = iR = 0,37(25t — e~^mt) • 500 = 185(е^-25* - - «г'⁰⁰') В, u_L = Ldi / dt = 4 ? 0,37(-25е ^25? + 100t> ¹⁰⁰0 = 37(4e¹⁰⁰' - e~^25t), u_c = -idt =.

c

• -5—- f 0,37(e^_25f — e-¹⁰⁰' )dt = 37(⁰' - 4e-²⁵').
• 100-lO-^{6 J}

Ответы, полученные при решении задачи классическим и операторным методами, совпадают, как и должно быть.

Задача 7.8. Цепь по рис. 7.11, б при нулевых начальных условиях подключается ключом К к постоянному напряжению U. Определить законы изменения тока i₂ и напряжения на конденсаторе и_с, если известны: U= 110 В, = 80 Ом, L = 0, R₂ = 500 Ом,.

С= 1 мкФ. Задачу решить с использованием табл. 7.1 и теоремы разложения. Решение задачи с использованием табл. 7.1

Запишем изображение искомого тока: L (v) = U (v) /Z (v). где U (v) = U/ v = 110 / «,.

Преобразуем I (p) так, чтобы получить изображения, имеющиеся в табл. 7.1:1_х(р)

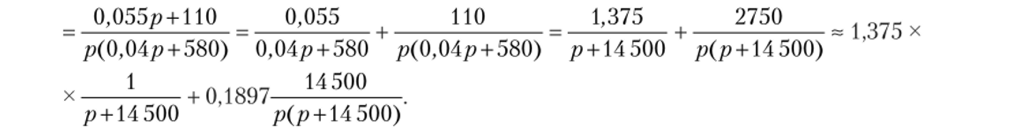
Согласно табл. 7.1, последним изображениям соответствуют оригиналы 1,375е~^14 500г и 0,1897(1 — е~^и 500t). Это означает, что.

Оригинал и_с, согласно табл. 7.1, запишется так:

Проверка: при t = 0 в соответствии с формулами (б) и (в) 1] = 0,1897 + 1,1853 = = 1,375, и_с = 0.

В первоначальный момент после коммутации в цепи обкладки конденсатора «замкнулись» между собой, и его сопротивление R_c= 0. Поэтому R_c= 0 шунтирует R-, и ток г,(0) ограничивается лишь ft, т. е. г,(0) = (// ft, = 110 / 80 = 1,375. Что касается и_с{0), то, с одной стороны, оно равно ft_f; — г, (0) = 0 • г,(0) = 0, с другой, согласно второму закону коммутации, -и_с(()) = %(0₊) = и_с(0) = 0.

Решение задачи с использованием теоремы разложения

Из выражения (а) имеем:

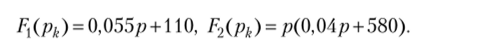
Из равенства F₂(p_k) = p (Q, Q4p + 580) = 0 находим корни: р_х = 0, р₂ = -14 500. Определяем производную:

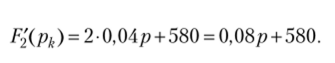
Подставив корни, определяем: /•', (/;,) = 0,055 -0+110=110, /-', (/;-,) = 0,055 (-14 500) + + 110 = -687,5; ft₂'(p,) = 0,08 • 0 + 580 = 580, ft₂'(p₂) = 0,08 (-14 500) + 580 = -580.

По теореме разложения находим искомый ток: i,(t) = У е^р= ——ь

к=Щ (Рк) ⁵⁸⁰

+ ~^687,5 g-2500f ₌ (0,1897 — 1,1853е^-2500').

—580.

Определяем искомое напряжение на конденсаторе. Из выражения U (j>) имеем:

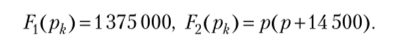
Из равенства ⁼ Р (Р ^00) = 0 находим корни: р_х = 0, р₂ = -14 500. Определяем производную:

Подставив корни, определяем: F,(p,) = F_x(j)₂) = 1 375 000, ft₂(p,) = 2−0+ 14 500 = = 14 500, F.₂(jh) = 2 • (-14 500) + 14 500 = -14 500.

И p (p

По теореме разложения находим искомое напряжение: и_с = У ,^к[ е^рь* =

*=i F₂(p_k)

1 375 000 1 375 000 _nton,_{t 1ХКППЧ}

=-±e^-1450t = 94,82(1 — е~^14 5000.

14 500 -1450.

При решении задачи с использованием табл. 7.1 и теоремы разложения ответы совпали, как и должно быть.

Классический и операторный методы расчета переходных процессов в линейных цепях являются универсальными, они могут применяться для решения задач любой сложности.

В частных случаях, когда воздействующее на цепь напряжение имеет сложную форму или приходится решать дифференциальные уравнения высоких степеней (например, выше третьей), считается целесообразными применять методы с использованием интеграла Дюамеля или спектральный, которые подробно рассматриваются в автоматике и других курсах.