Энергетика химических реакций

I. Значение темы Химическая термодинамика является теоретической основой химии. Она представляет собой математическую модель реальных систем, позволяющих решить вопрос о возможности протекания различных процессов. Знание термодинамических закономерностей позволяет получить представления об энергетическом балансе человеческого организма, установить специфические особенности преобразования одних видов энергии в другие в процессе жизнедеятельности. Полученные знания способствуют более глубокому усвоению многих разделов неорганической химии (химическая кинетика, химическое равновесие, учение о растворах), а также других химических и профильных дисциплин.

II. Теоретические сведения Тепловые эффекты являются важными характеристиками химических реакций. По их величинам можно судить о том, будет ли в течение реакции некая система нагреваться или охлаждаться и на сколько.

Химические процессы, протекающие в живых организмах, а также большинство химических реакций осуществляются в условиях постоянного давления (p = const). Энергия, которой обладает система, находящаяся при постоянном давлении (изобарный процесс) называется энтальпией.

Энтальпия — это сумма внутренней энергии системы и произведения объема на давление:

Энтальпия — это функция состояния и в термодинамических расчетах используют изменение энтальпии между конченым и начальным состоянием:

.

где Н₁ — энтальпия начального состояния системы;

Н₂ — энтальпия конечного состояния системы Если реакция экзотермическая, то энергия выделяется из системы, что ведет к уменьшению энтальпии, то есть Q>0, a ДH<0. Если реакция эндотермическая — тепло поглощается системой, то есть Q<0, a ДH>0. Таким образом, тепловой эффект реакции Q и энтальпия Н противоположны по знаку:

Из второго закона термодинамики следует, что внутренняя энергия системы состоит как бы из двух частей: свободная энергия — та часть внутренней энергии, которая может быть использована для совершения работы, и связанная энергия — та часть внутренней энергии, которая не используется для совершения работы, а бесполезно рассеивается в виде тепла. Связанная энергия определяется энтропией S, которая равна или:

(при постоянной Т).

Чем больше энтропия, тем больше количество связанной энергии, а чем больше в системе связанной энергии, тем более необратимым является процесс.

С точки зрения статистической термодинамики, энтропию можно рассматривать как меру беспорядка или наиболее вероятного состояния системы:

.

где W — вероятность существования вещества;

К — постоянная Больцмана:

.

где R — газовая постоянная;

N_A — число Авогадро Энтропия также, как и энтальпия, является функцией состояния, то есть определяется начальным и конечным состоянием.

Энтальпийный и энтропийный факторы. Энергия Гиббса

Самопроизвольное направление реакции определяется действием двух факторов:

• 1) тенденцией системы к переходу в состояние с меньшей внутренней энергией (энтальпийный фактор);
• 2) тенденцией к достижению наиболее вероятного состояния, которое достигается переходом системы из более упорядоченного состояния в менее упорядоченное (энтропийный фактор).

Таким образом, движущая сила любого процесса определяется разностью энтальпийного и энтропийного факторов при постоянном давлении и температуре, и называется энергией Гиббса:

.

где.

Знак ДG определяет направление процесса. При ДG<0 процесс идет в прямом направлении, ДG>0, процесс идет в обратном направлении, ДG=0, условие термодинамического равновесия, при котором в системе не происходит ни энергетических изменений, ни меняется степень беспорядка.

Критерии направления самопроизвольно протекающих процессов

Из уравнения можно выявить критерии направления самопроизвольных реакций.

III. Вопросы для самоконтроля.

• 1. Что изучает химическая термодинамика?
• 2. Какими энергетическими эффектами могут сопровождаться химические реакции?
• 3. Какие процессы называются изохорными, изобарными, изотермическими?
• 4. Что характеризует внутренняя энергия и энтальпия?
• 5. Что называется теплотой образования, сгорания, разложения веществ?
• 6. Каким уравнением определяется энтальпия и ее изменение?
• 7. Какой закон является основным законом термохимии? Дайте его формулировку.
• 8. Перечислите следствия, вытекающие из закона Гесса.
• 9. Дайте определение понятия энтропия. Характер изменения энтропии. Единицы измерения. Уравнение Больцмана.
• 10. Как изменяется энтропия прямой и обратной реакции синтеза аммиака?
• 11. Сформулируйте второй закон термодинамики.
• 12. Какие значения принимает ДG при:
  • а) наступлении состояния равновесия;
  • б) реакции, протекающей в сторону образования конечных продуктов?
• 13. Возможно ли самопроизвольное протекание реакции, если при положительном значении ДS:
  • а) ДН>0;
  • б) | ДН|>|T•ДS |

IV. Задачи с эталонами решения.

Пример 1:

При сгорании 1 моль ацетилена в кислороде выделилось 1300 кДж теплоты. Определите теплоту образования ацетилена, если стандартные теплоты образовании СО₂ (г) и Н₂О (ж) равны 393,5 кДж/моль и 286 кДж/моль соответственно.

Решение:

Рассчитываем теплоту образования ацетилена по уравнению:

кДж Отсюда можно записать:

Отсюда находим:

кДж Ответ: Теплота образования С₂Н₂ равна 227кДж/моль.

Пример 2:

При горении формальдегида выделяется 561 кДж тепла. Вычислите теплоту образования формальдегида, если теплота образования СО₂ равна 393,6 кДж/моль, а теплота образования Н₂О (г) — 242 кДж/моль.

Решение:

По первому следствию из закона Гесса записываем:

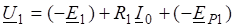
Ответ: Теплота образования формальдегида равна 74,6кДж.

Пример 3: Задача на закон Гесса Вычислить ДНр окисления этанола до уксусной кислоты:

.

если известно, что в организме эта реакция протекает в две стадии:

1).

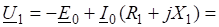
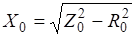
Решение:

Для решения нужного уравнения необходимо к первому уравнению прибавить второе и сократить подобные члены:

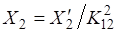
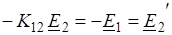
Пример 4:

Определите как изменится энтропия в следующей реакции:, полученный ответ подтвердите расчетами, если:

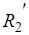
Решение:

ДS<0, так как в реакции число молей веществ, а газообразном состоянии уменьшается, значит энтропия тоже уменьшается (S₁>S₂).

По первому следствию из закона Гесса:

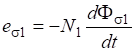
Пример 5:

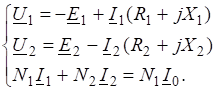
Рассчитаете ДG реакции, если, а. Возможна ли эта реакция в стандартных условиях?

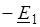
Решение:

Используем уравнение Гиббса:

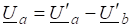
ДG<0, реакция идет в прямом направлении.

Пример 6:

Повлияет ли изменение температуры (повышение и понижение) на направление протекания реакции, если ДН<0, S>0. (Проанализируйте уравнение Гиббса).

Решение:

При условии ДН<0, а ДS>0 ДG<0 при любых температурах (при высоких и при низких температурах).

V. Задачи для самостоятельного решения.

1. Вычислите ДН⁰ реакций (см. приложение):

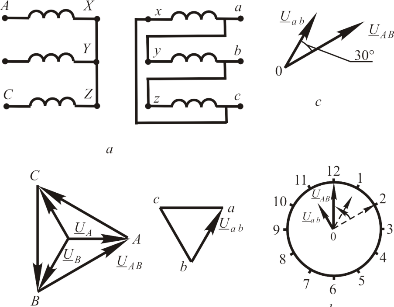
• 2. При сгорании 2 моль этилена в кислороде выделилось 2822кДж теплоты. Определите теплоту образования этилена, если стандартные теплоты СО₂ и Н₂О равны 393 кДж/моль и 286 кДж/моль соответственно.
• 3. Исходя из теплот реакций окисления As₂O₃ кислородом и озоном

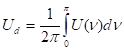
Вычислите теплоту образования озона из молекулярного кислорода.

4. Не производя вычислений установите знак ДS⁰ следующих процессов:

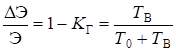
• 5. В каком из следующих случаев реакция возможна при любой температуре (проанализируйте уравнение Гиббса):
  • а) ДН<0; ДS>0;
  • б) ДН<0; ДS<0;
  • в) ДН>0; ДS>0;

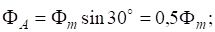
6. На основании значений и реагирующих веществ (см. приложение) вычислите ДG следующих процессов:

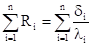
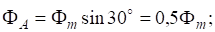
Укажите в каком направлении эти реакции будут протекать.

VI. Литература для самоподготовки.

• 1. Ю. А. Ершов, В. А. Попков и др. Общая химия. — М., 1993. — с. 10−21
• 2. Н. А. Глинка. Общая химия. — Л., 1979 и др. — гл VI, с. 166−170, 195−204.
• 3. А. С. Ленский Введение в бионеорганическую и биофизическую химию. — М., 1989. — с. 6−22
• 4. Лекции.