Свойства логистического отображения

Рассмотрим свойства отображения.

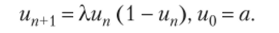
Заметим, так как /(0) =/(1) = 0 и max f (x) = /(0,5) = Х/А, то при 0 < X < < А интервал I = [0; 1] отображается в себя, х е I.

Введем обозначения.

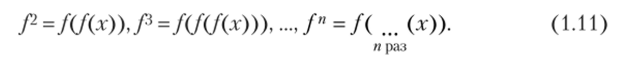
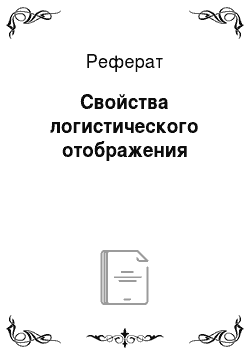
При заданном начальном значении и₀ однозначно определяются все значения и_п. Будем говорить, что множество всех пар (я, и_п) образует траекторию отображения. В более узком смысле под траекторией будем понимать последовательность значений всех степеней отображения {/'4^wo)}≅oОпределение 1.1. Точка а е X, где X — множество, включающее в себя все значения отображения (1.11), называется предельной точкой траектоpuu {fⁿ(u₀)}~₌₀, если существует последовательность n_x < n₂< … < n_k, n_k^> °° при k —" oo, такая что fⁿk —> я, k = 1, 2,…

1. Рассмотрим случай 0 < X < 1. Тогда на I = [0; 1 ] существует только одна предельная (или неподвижная) точка х = 0, т. е. любая последовательность {/'4^wo)}≅o сходится к предельной точке рассматриваемого отображения х = 0. Если рассматривается популяционная модель, то это означает, что рассматриваемая популяция не может выжить.

Несложно показать, что последовательность {м"}~₌₀ сходится к своей предельной точке, если.

В этом случае предельная точка называется притягивающей. При выполнении условия.

точка называется отталкивающей.

В пограничном случае |/_м'| = 1 об устойчивости предельной точки сказать ничего нельзя. Если значение производной непрерывно зависит от параметра (как в случае рассматриваемого логистического отображения) и производная при каком-то значении параметра принимает значение 1, то при дальнейшем изменении параметра тип устойчивости предельной точки меняется. В этом случае принято говорить, что происходит бифуркация, а значение параметра называется бифуркационным.

Определение 1.2. Пусть при некотором q < 1 отображение у = f (u) удовлетворяет условию ~ f (u₂)| < qu_{ — и₂[ Тогда рассматриваемое отображение называется сжимающим.

Теорема 1.1. Если отображение у = f (u) — сжимающее, то уравнение и = f (u) имеет решение u=V, где V является предельной точкой разностного отображения и_п+] = f (u_n). При этом выполняется неравенство

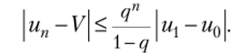
Доказательство. Пусть рассматриваемое отображение сжимающее. В этом случае.

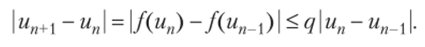
Далее,.

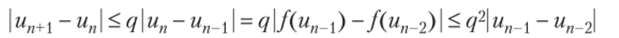
и т.д. Значит,.

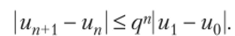
При некотором 1> п имеем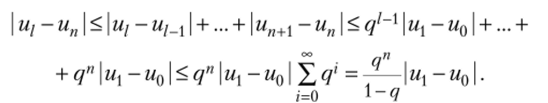

В соответствии с критерием Коши последовательность и" имеет некоторый предел V при п —> при переходе к которому получаем.

Далее,.

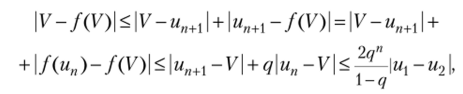
откуда следует | V— /(V) = 0, или V=f (V), поскольку п произвольное. •.

Очевидно, что при q > 1 V не будет решением рассматриваемого уравнения.

В вычислительной математике подобный процесс (нахождения предельной, или неподвижной, точки отображения) называется итерационным методом нахождения корня алгебраического уравнения, имеющего, в рассматриваемом случае, вид.

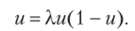
Графическое изображение этого процесса при X < 1 представлено на рис. 1.1. В этом случае на отрезке [0; 1] имеется сходимость к единственной устойчивой неподвижной точке х = 0.

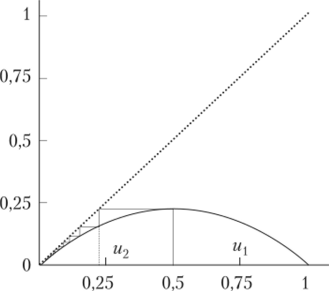
Рис. 1.1. Итерационный процесс в случае X < 1 (начальное приближение щ = 0,5).

Начертим графики функций у = f (u) = Хи ( 1 — и) и у = и. Отложим м₀ на оси Ох, проведем перпендикуляр до пересечения с графиком первой функции, затем — горизонталь до пересечения с графиком второй функции. Почти очевидно, что и₂ = /(мД.

Далее этот процесс можно продолжить для всех точек и₂, щ, …, и", … В результате получается так называемая диаграмма Ламерея, сходящаяся к и = 0, т. е. > 0 при Случай Х = 1 от представленного на рисунке качественно не отличается. В этом случае в неподвижной точке имеет место касание графиков функций, сходимость к неподвижной точке будет сколь угодно медленной.

2. Рассмотрим случай 1 < X < 3. Если X > 1, то неподвижная точка и = О становится отталкивающей, поскольку |/'(0)| > 1, а на [0; 1 ] появляется другая неподвижная точка w¹ = 1 — Х~К

Для рассматриваемого отображения f'(u^{) = |2 — Х < 1, так как f'(u) = = А,(1 — 2и); значит, точка и^{ при 1 < X < 3 является притягивающей.

Отметим, что при 1 < X < 2 f'(u^{) > 0, решение V= 0 теряет устойчивость, но есть сходимость ко второй устойчивой неподвижной точке: траектория {fⁿ(^uo))n=1 монотонно стремится к и^{ (рис. 1.2). При X > 2 производная отображения меняет знак, теперь f'(u^{) < 0 и траектория приближается к и^{ немонотонно, поочередно принимая значения то меньше, то больше этого значения.

или.

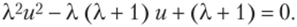
Заметим, что если и' — предельная точка отображения f (u) = и_у то она является также и предельной точкой отображения f²(u) = и, так как.

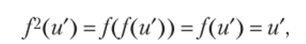
где и' — любая предельная точка рассматриваемого отображения, отличная от корней уравнения /²(«) = и:

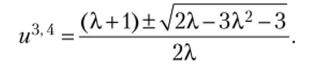
Эти корни связаны соотношениями /(г/³) = u^A, f (u^A) = и³.

В этом случае говорят, что отображения имеет цикл периода 2, который будем обозначать Р₂. Его наличие, например, в популяционной модели говорит об изменении численности особей с периодом в два года.

Переход от цикла Р, (предельная точка логистического отображения) к циклу Р₂ называют бифуркацией удвоения периода. Цикл периода 2 изображен на рис. 1.3. В этом случае обе неподвижные точки неустойчивы.

или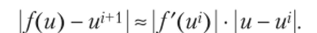

Но поскольку f^m(u) является сложной функцией, то получим.

В таком случае, если.

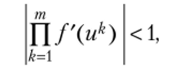
то траектория {/'4^wo)}"=o приближается к циклу {г/¹, и^т}, или {u^k}f_=v Этот цикл будет притягивающим. В общем случае цикл может быть как притягивающим, так и отталкивающим.

Определение 1.4. Цикл Р_т = {и¹, …, и^т) отображения /: X —> Х_у переводящего множество X в себя, называется притягивающим, если существует е-окрестность этого цикла 5_е, такая что для любой точки этого отображения и_п е S_c траектория {/" (^wo)}≅ ₀ распадается на т последовательностей, каждая из которых сходится к точкам м¹,…, и^т соответственно.

Определение 1.5. Цикл Р_т = {г/¹, …, м" ^;} называется отталкивающим, если существует его со-окрестность 5_W, такая что для каждого и е S_i0 выполнено /"(«)(») ?

Достаточным условием существования притягивающего (отталкивающего) цикла является выполнение неравенства.

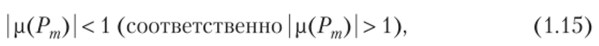
где.

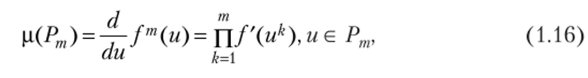
— мультипликатор цикла.

Отмстим интересные свойства функции Р (и), в частности тот факт, что ее график пересекается с прямой у = и не только в неподвижных точках рассматриваемого отображения г/¹, и², но и в точках цикла Р₂: и³, w⁴. Таким образом, можно сказать, что переход Pj —> Р₂ обусловлен потерей устойчивости одной предельной точки и появлением двух устойчивых предельных точек отображения.

На рис. 1.4, а, б показано поведение функции р (и) при разных значениях X: а) X = 2,8; б) X = l + V5. В первом случае неподвижная точка соответствует устойчивой неподвижной точке отображения /(и), во втором — неустойчивой неподвижной точке отображения f (u) и точкам цикла периода 2.

При увеличении X у отображения появляются новые неподвижные точки. Мультипликатор цикла Р₂ вычисляется следующим образом:

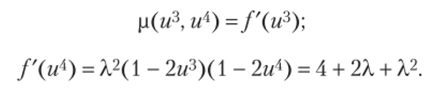
Очевидно, что |р (гг³, г/⁴) | < 1, если 3< А,< 1 +Тб, т. е. цикл Р₂ — притягивающий. Это означает, что траектория {/" (гг)}~₌₀ притягивается циклом {г/³, гг⁴} таким образом, что подпоследовательность {/^2,7(гг₀)}~₌₀ сходится к одной точке цикла, a {/^2w+1(^wo)}/T=o ^— к Другой.

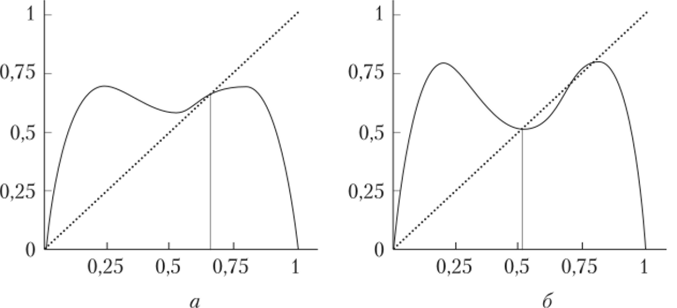
Рис. 1.4. Неподвижные точки отображения/Чм) в случаях:

a- = 2&6-X = + S

Знак мультипликатора (1.16) дает информацию о характере приближения траектории к циклу. В частности, если р>0иЗ<�Х<1 + V5, то подпоследовательности {/^2 м(и₀)}~₌₀ и {/²" ⁺¹(w₀)}~₌₀ начиная с некоторого и являются монотонными, одна возрастает, другая убывает, что зависит от знаков /'(и³) и f'(u^A).

При 1 + >/5<^<1 + %/б значение мультипликатора р < 0, и подпоследовательности {/²" ⁺¹(^wo)}w=0' {/^2w(^wo)}w=o приближаются к и³, и^А с разных сторон.

4. Случай 1 + л/б <�Х<3,54…. При А, = 1 + л/б происходит следующая бифуркация: цикл {и³ w⁴} из притягивающего превращается в отталкивающий (| р (г/³, и^А)| > 1 при X > 1 + Тб). Появляется новый притягивающий цикл Р₄:

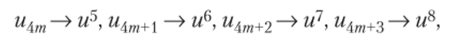
причем.

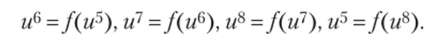
С позиции популяционной динамики это означает, что численность особей колеблется с периодом четыре года. Соответствующая диаграмма Ламерея приведена на рис. 1.5.

5. При X ~ 3,54 цикл Р₄ периода 4 становится отталкивающим, так как |р (и⁵,…, и³) | > 1. При этом появляется притягивающий цикл Р₈ периода 8. Дальнейшее увеличение параметра X будет приводить к появлению циклов Р_1б, Р₃₂ и т. д.

Заметим, что рассмотренный нами простой процесс имеет весьма сложное поведение, суть которого до конца, по-видимому, еще не ясна. Мы наблюдаем каскад бифуркаций при увеличении величины X. Кроме того, все циклы, которые при этом встречаются, имеют период 2р. Это важнейшая закономерность, наблюдающаяся не только в расчетах, но и в природе!

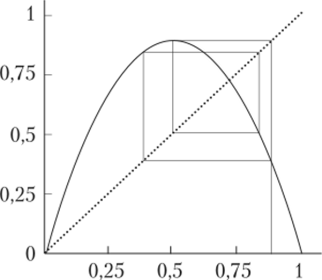
Рис. 1.5. Диаграмма Ламерея для устойчивого цикла периода 4.

Рассмотренные бифуркации при увеличении X можно представить с помощью бифуркационной диаграммы (рис. 1.6). Она получается, если обозначить через А_{} Д₂,… те значения X, в которых происходят бифуркации, а через X_jf Х₂,… — те, при которых величина и = 0,5 является элементом циклов Р₂, Р^у…. На практике по оси ординат откладываются все значения элементов последовательности в установившемся режиме, т. е. итерации начинаются с произвольного начального приближения. Значения первых N итераций отбрасываются (обычно N = 1000), а остальные значения при данном X отмечаются точками на диаграмме. По оси абсцисс откладывается значение параметра отображения.

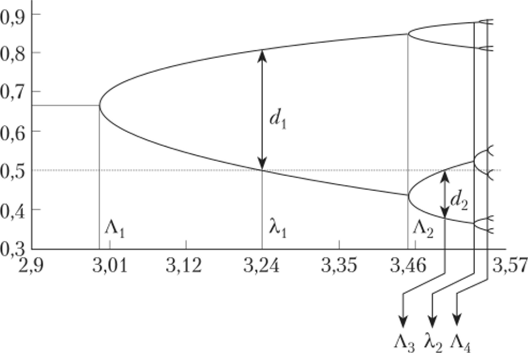
Рис. 1.6. Бифуркационная диаграмма логистического отображения (схема).

Обозначим через d_x, d₂,… величины, равные расстоянию между и = 0,5 и ближайшим к нему элементом цикла Р₂" при X = Х_п (см. рис. 1.6). Численный эксперимент показал, что А_п и Х_п при достаточно больших п ведут себя как геометрическая прогрессия со знаменателем 5 = 4,66 920…, т. е.

Отношение d_n/d_n+{ имеет предел, ранный, а = 2,50 290…. Эти закономерности были замечены американским математиком М. Фейгенбаумом. Постоянная 8 носит название константы Фейгенбаума.

При дальнейшем увеличение X последовательность {м"}~₌о приобретает хаотический характер (при Х = Х₀₀~ 3,569), что видно на рис. 1.7 (на рисунке опущена часть диаграммы, соответствующая X < 2).

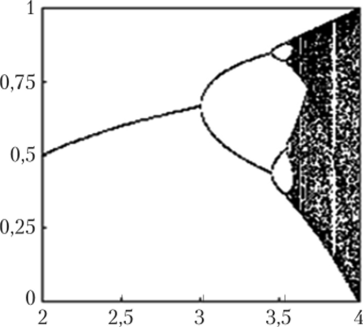
Рис. 1.7. Бифуркационная диаграмма логистического отображения, построенная в результате численных расчетов (каскад Фейгенбаума).

Примечательно, что эти так называемые каскады Фейгенбаума имеют фрактальный характер, т. е. обладают масштабной инвариантностью. Малый фрагмент каскада Фейгенбаума в точности повторяет целый каскад (рис. 1.8, а, б).

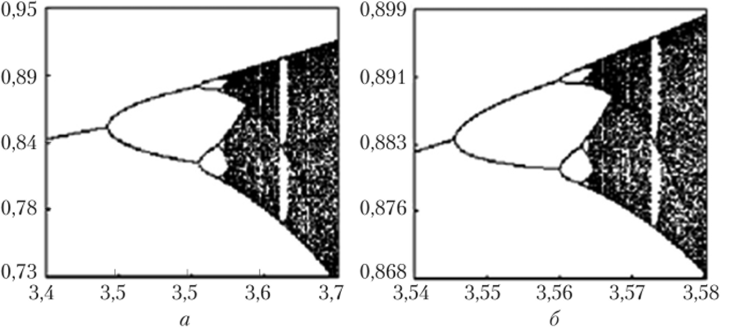
Рис. 1.8. Увеличенные фрагменты каскада Фейгенбаума.

Изучение графиков функций f²(x) иР (х) показывает, что их фрагменты вблизи максимумов подобны друг другу, более того, они отличаются лишь масштабами. Оказывается, что такое же подобие имеет место для функции /²", п > 1, при X = Х_п, причем выполняется тем точнее, чем больше п.

Если положить и' = и — ½ (в дальнейшем штрих будем опускать) и считать а коэффициентом растяжения вдоль осей, то для некой симметричной функции g (x)_} определенной на отрезке [-1; 1 ], можно получить функциональное уравнение:

которое универсально определяет ос, g (0) = -ag'(O).

Вблизи максимума g (x) должна быть близка к квадратичной параболе, причем g (0) = 1. В так называемой теории универсальности показывается, что g (x) вычисляется рядом:

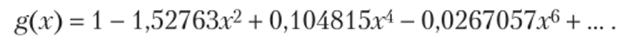
6. Рассмотрим случай X = 3,83. В этом случае из хаотической области, изображенной на рис. 1.7, появляется устойчивый цикл Р₃.

На рис. 1.9, а — в представлены различные циклы после 15 итераций. Циклу Р₃ на рис. 1.7 соответствует самое большое «окно» устойчивых циклов Р Это явление — чередование хаотических и регулярных зон — называется перемежаемостью. Возможно, нечто подобное наблюдается в гидродинамических потоках, где ламинарные зоны чередуются с турбулентными^[1].

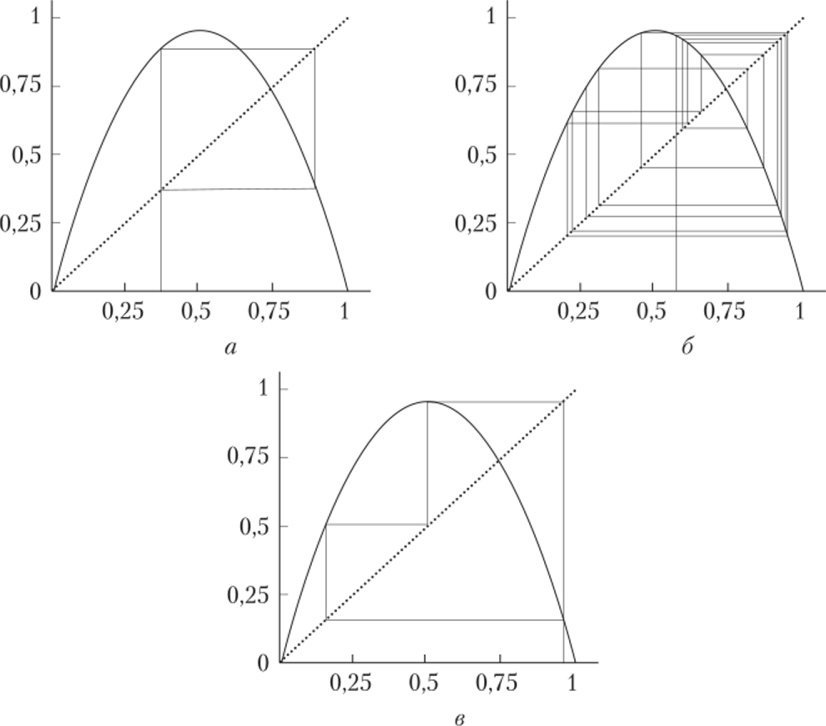
Рис. 1.9. Лестницы Ламерея для нескольких последовательных итераций.

логистического отображения:

а — для устойчивого цикла периода 2; б — для цикла большого периода (большего, чем показанное на рисунке количество итераций); в — для цикла периода 3.

Аналогичными свойствами обладают некоторые другие дискретные отображения. Так, каскад бифуркаций удвоения периода, циклы периодов 3 и 5, хаотические колебания можно наблюдать в отображениях.

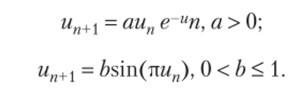
Переход к хаотическим колебаниям в этих отображения тоже осуществляется по сценарию Фейгенбаума. Для этих отображений также справедлива формула (1.17)^[2].

• [1] Ландау Л. Д., Лифшиц Е. М. Гидродинамика. М.: Физматлит, 2006.
• [2] Более подробно класс дискретных отображений, эквивалентных по своим свойствамлогистическому, рассмотрен в работе: Майстренко Ю. Л., Романенко Е. Ю., Шарковский Л. Н. Указ. соч.