Расчет и анализ динамических процессов разомкнутой системы электропривода

Структурная схема системы ПЧ-АД

Переходным процессом называется режим работы электродвигателя при переходе из одного установившегося состояния в другое, сопровождающееся изменением его тока, момента, частоты.

При этом уравнение равновесия имеет вид [1]:

(3.1).

При математическом описании мы имеем право пренебречь электромагнитной постоянной времени и считать переходные процессы электромеханическими, так как при питании от преобразователя частоты асинхронный электродвигатель работает исключительно на прямолинейных участках механических характеристик.

Так как в системе ПЧ-АД электродвигатель работает только при скольжениях, меньших критического, то является целесообразным использовать математическое описание прямолинейного участка характеристики, которое можно представить следующим образом:

= он —, (3.2).

где он — скорость идеального холостого хода при частоте f, равной номинальной частоте fн;

= f / fн — относительная частота напряжения питания;

— статическое падение скорости.

Так как на рабочем участке механические характеристики двигателя в системе ПЧ-АД параллельны, то при данном Мс статическое падение скорости является величиной постоянной, то есть (3.2) можно представить в виде:

= он — К М, (3.3).

где К — коэффициент пропорциональности между М и .

Этот коэффициент можно определить, исходя из следующих соображений: он является постоянным для любой точки характеристики, в том числе и для точки номинального режима на естественной характеристике, то есть из (3.3) можно записать н = он — К Мн. (3.4).

Из (3.4) после алгебраических преобразований получаем:

К = он Sн / Мн. (3.5).

Подставляем в (3.3) вместо К его значение из (3.5) и после алгебраических преобразований получаем математическое описание момента двигателя на линейных участках механических характеристик:

М = (он —) Мн / Sн он. (3.6).

Дальнейшее математическое описание целесообразно вести в относительных единицах (здесь относительные величины обозначаются значком *); в качестве базовых используются: Мн, он, fн.

Тогда (3.6) принимает вид:

М* = (- *)/ Sн. (3.7).

Из уравнения движения электропривода получаем:

М = Мс + Тм (Мкн / он)(d / dt), (3.8).

где Тм = J он / Мкн — электромеханическая постоянная времени;

Мкн — критический момент на характеристике при f = fн.

Представим (3.8) в относительных единицах:

М* = Мс* + Тм (Мкн / Мн) (d* / dt). (3.9).

Здесь Мкн / Мн = - перегрузочная способность двигателя. Причем закон совместного изменения частоты и напряжения преобразователя выбирается именно из условия получения постоянной перегрузочной способности при любой форме зависимомти от скорости момента статического, то есть для всех реально возможных режимов эта величина остается неизменной. Следовательно (3.9) можно записать:

М* = Мс* + Тм (d* / dt). (3.10).

Определим из (3.10) d* / dt и представим полученное уравнение и (3.7) в операторной форме:

* (р) =(М*(р) — Мс* (р)). (3.11).

М*(р) = ((р) — *(р)) / Sн. (3.12).

На основании (3.11), (3.12) построена структурная схема асинхронной машины при ее работе на прямолинейных участках механических характеристик, приведенная на рис. 3.2.

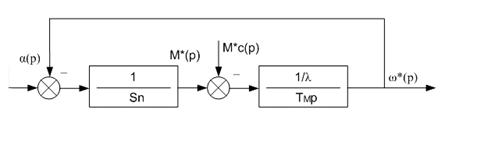
Рис. 3.1. Структурная схема асинхронной машины

Как указывалось выше, преобразователь частоты состоит из выпрямителя и инвертора, соединенных последовательно. Если, согласно 8, представить их апериодическими звеньями с постоянными времени Тв и Ти соответственно, то передаточная функция Wп (p) преобразователя имеет вид:

Wп (p) = Кп / [(Tв + 1)(Tи p+1)], (3.13).

где Кп — коэффициент усиления ПЧ.

После алгебраических преобразований (3.13) можно записать.

Wп (p) = Кп / (TвТи p2+Tв p+Tи p+1). (3.14).

Как указывалось выше, постоянная времени выпрямителя Тв = 0,01с, а величина постоянной времени инвертора определяется его конструкцией.

Если инвертор построен на базе тиристорных ключей, то его постоянная времени Ти = 0,01, если — на базе тразисторов, то его можно считать безъинерционным звеном с постоянной времени равной нулю. Если Ти = 0,01, то TвTи = 0,0001с. Этой величиной можно пренебречь и тогда.

Wп (p) = Кп / [(Tв+Tи)p+1)]. (3.15).

Следовательно,.

Wп (p) = f (р) / Uз = Кп / [(Tв+Tи)p+1)]. (3.16).

Представим (4.63) в относительных единицах, где базовым значением Uз является Uзн, при котором на выходе преобразователя имеется напряжение с частотой fн, равной номинальной. Имея в виду, что в установившемся режиме UзнКп = fн, получаем:

(р) = U*(р) / [(Tв+Tи)p+1)]. (3.17).

На основании (3.17) с учетом схемы рис. 3.1 строится структурная схема разомкнутой системы ПЧ-АД, приведенная на рис. 3.2.

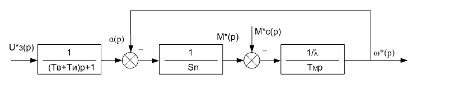
Рис. 3.2. Структурная схема системы ПЧ-АД

Эта система описывается следующими дифференциальными уравнениями:

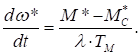
(3.2).

(3.3).

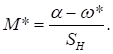
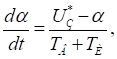
(3.4).

где *=/он — относительная скорость;

_он — скорость идеального холостого хода при частоте f=f_н;

М^*=М/М_н — относительный момент;

^* = f/f_н — относительная частота;

U_З^*=K_З· t, где K_З=1/tn — коэффициент скорости изменения частоты выходного напряжения преобразователя;

S_н — номинальное скольжение асинхронной машины.