Формула полной вероятности и формула Байеса

Пусть имеется полная система событий А 4- … + А_п = П, A{Aj = 0 для i ф j. Тогда любое событие В можно представить в виде суммы непересекающихся событий В = ВА + … + ВА_п и, следовательно,.

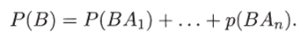
Вспомнив правило умножения, можно записать.

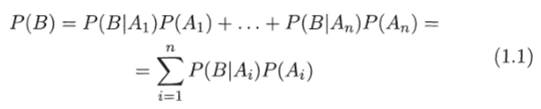
— формула полной вероятности.

Пример 1.5. Пусть имеются три трудноразличимые при диагнозе болезни А, Л₂, Аз, встречающиеся с частотой 50, 40 и 10%, и есть метод лечения В, приводящий к успеху соответственно в 70, 75 и 90% случаев. Какова вероятность излечения для пациента, страдающего одной (неизвестно, какой именно) из болезней А, А? или Лз?

Имеем Р (Л,) = 0,5; Р (Л₂) = 0,4; Р (Л₃) = 0,1; Р (В|Л0 = 0,7; Р (В|Л₂) = 0,75; Р (В|Л₃) = 0,9. Получаем: Р{В) = 0,5−0,7+0,4х хО, 75+ 0,1−0,9 = 0,74.

Из соотношений, полученных в соответствии с правилом умножения P (AiB) = Р (В|Л*)Р (Л_{) и Р (Л*В) = Р (Л;|В)Р (В), находим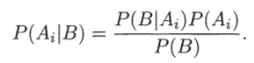

Заменив Р (В) в знаменателе по формуле полной вероятности, получаем формулу Байеса, или формулу вероятностей гипотез:

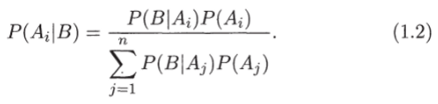
Вероятности Р (Лг), г = 1, …, п, в данном контексте носят название априорных вероятностей гипотез Л*, а вероятности Р (Лг|В), i = 1, …, п, называются апостериорными вероятностями гипотез А,. Формула Байеса, таким образом, позволяет, исходя из результатов эксперимента, корректировать имеющиеся знания о вероятностях интересующих нас событий.

Пример 1.6. Рассмотрим данные примера 1.5, изменив вопрос. Предположим, что лечение по методу В оказалось успешным. Какие выводы можно сделать на основании этого факта относительно диагноза? Формула Байеса дает следующие результаты:

Итак, вероятность диагноза А несколько снизилась, а вероятность диагноза повысилась, что естественно, поскольку лечение В более эффективно при болезни А%.

Задачи для самостоятельного решения

• 1. Предположим, что 5% всех мужчин и 0,25% всех женщин дальтоники. Наугад выбранное лицо оказалось дальтоником. Какова вероятность того, что это мужчина? (Считать, что мужчин и женщин одинаковое число.)
• 2. При рентгеновском обследовании вероятность обнаружить заболевание туберкулезом у больного туберкулезом равна 0,9. Вероятность принять здорового человека за больного равна 0,01. Пусть доля больных туберкулезом по отношению ко всему населению равна 0,001. Найдите вероятность того, что человек здоров, если он был признан больным при обследовании.
• 3. Среди 25 экзаменационных билетов 5 «хороших». Два студента по очереди берут по одному билету. Найдите вероятности следующих событий: А — первый студент взял «хороший» билет; В — второй студент взял «хороший» билет; С — оба студента взяли «хорошие» билеты.
• 4. Ваши друзья могут с равной вероятностью играть в одну из двух игр. В одной игре используется одна игральная кость, в другой — две игральные кости. Счет в любой игре равен количеству очков, выпавших на одной кости, или на обеих костях вместе. Вы слышите, что в какой-то игре у них выпало два очка. Какова вероятность того, что они играют в игру с одной костью?
• 5. В первой урне 8 белых и 2 черных шара, во второй урне 16 черных шаров. Из каждой урны наудачу извлекли по одному шару, а затем из этих шаров наудачу взят один шар. Найдите вероятность того, что он белый.
• 6. В родительской популяции генотипы АА, Аа, аа встречаются с частотами р², 2pq, q², соответственно р + q = 1. Найдите распределение генотипов потомков (предполагается случайное скрещивание).
• 7. Найдите три вероятности того, что потомок имеет генотип А А, если одна из родительских особей (мужская или женская) имеет генотип: (1) А А, (2) Аа, (3) аа. Другая родительская особь имеет один из генотипов АА, Аа, аа. В родительской популяции генотипы АА, Аа, аа

встречаются с частотами р², 2pq, q², соответственно, и р + q = 1 (предполагается случайное скрещивание).

8. В родительской популяции генотипы АА, Аа, аа встречаются с частотами р², 2pq, q², соответственно, и р + q = 1 (предполагается случайное скрещивание). Известно, что их потомок имеет генотип АА. Найдите вероятность того, что его брат имеет генотип Аа.