Основные теоремы теории пределов

Пользуясь установленным понятием предела последовательности комплексных чисел, мы можем перенести в комплексную область известные теоремы о пределах последовательностей действительных чисел. Так, если две данные последовательности комплексных чисел.

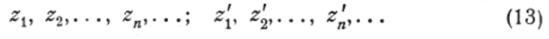
сходятся соответственно к числам z и z то, образуя новую последовательность чисел.

где положено w_n = г_п±z'_n или w_n-=z_n-z'_n} или w_n = —, (в последил нем случае z'_n Ф 0), мы убеждаемся, что эта последовательность (14) сходится и имеет своим пределом w, причём w = zzbz' или w= =z*z или w= р- (в последнем случае предполагается z' ф 0), г. е.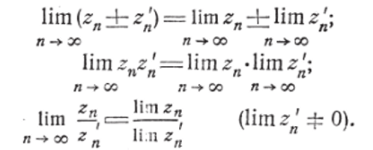

На доказательстве этих элементарных теорем теории пределов мы не останавливаемся, так как оно проводится аналогично доказательству соответствующих предложений теории пределов действительных чисел.

Критерий Коши.

Как известно из основ теории пределов, Коши дал критерий, характеризующий сходящуюся последовательность чисел. Этот признак Коши состоит в следующем: условие, необходимое и достаточное для сходимости последовательности комплексных чисел

заключается в том, чтобы при всяком сколь угодно малом положительном е существовало натуральное число N=N (e) такое, что неравенство z_N+m— z_N|<^е выполняется, каково бы ни было натуральное число т.

Геометрически этот критерий означает, что последовательность точек z_n будет сходящейся лишь в том случае, если все её точки, начиная с номера N, N=N{e), лежат внутри круга с центром в точке z_N радиуса е.

Необходимость этого условия доказывается весьма легко. В самом деле, если limz_n = z_t то найдётся такое число что при.

п -*? оо ^ У

имеет место неравенство |z—г_п<^~ .

Заметив, что z_N+m — z_N= (z_N+m—z)—(z—z_N), имеем:

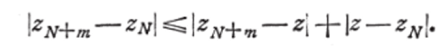
По условию будем иметь: 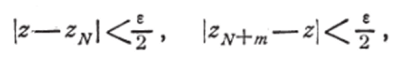следовательно,.

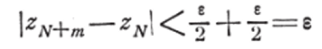
при ВСЯКОМ 0, что и нужно.

Покажем достаточность признака. Предполагая условие Коши выполненным, мы видим, что все точки последовательности (12), начиная с точки z_Ny лежат внутри круга радиуса е с центром в этой точке.

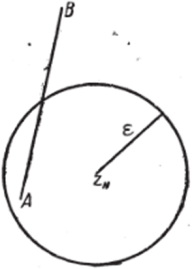
Фиг. 12.

Следовательно, наша последовательность точек (12) есть ограниченная. Остаётся показать, что она не может иметь двух различных предельных точек А и В. В самом деле, допуская противное, примем.

z<^rAB. Этому числу s соответствует нагураль;

ное число А/ = N (t) такое, что абсолютная величина разности z_N+_m — z_N е, т. е. все точки последовательности (12), начиная с точки z_N, лежат внутри круга с центром в точке z_N радиуса е (фиг. 12). Вне этого круга может находиться лишь конечное число точек данной последовательности, и, следовательно, обе предельные точки А и В должны лежать внутри круга или на его окружности. В таком случае расстояние между ними АВ должно быть не больше диаметра 2s, а мы приняли АВ > 2s, откуда следует противоречие. Итак, при выполнении условия Коши последовательность точек (12) сходится, так как она ограничена и не может иметь более одной предельной точки, а значит, — по теореме Больцано-Вейерштрасса (п. 4) — имеет одну предельную точку.