Экспериментальные расчеты на основе многопериодной биномиальной модели

Рассмотрим подробнее представленный выше метод определения текущей оценки будущих доходов на основе многопериодной биномиальной модели на следующем условном примере.

Пусть рассматривается некоторый рисковый проект инвестиций. Суммарные инвестиционные расходы, но проекту составляют 60 млн руб. Период полезного использования проекта равен четырем годам. Известно, что в текущем периоде этот проект принес бы базовую или текущую условную прибыль без учета условно-постоянных расходов в размере 80 млн руб., условно-постоянные расходы в текущем периоде составляют 70 млн руб. Теми инфляции примем равным 10% в год. Известно, что указанная условная часть прибыли может изменяться ежегодно, причем либо она возрастает с темпом роста 1,3, либо падает с темпом роста 0,9. Безрисковая ставка процента составляет 15%. Следует учесть, что условно-постоянные расходы по проекту будут меняться с учетом темпа инфляции. Ради простоты предположим, что темпы инфляции остаются постоянными в течение всего рассматриваемого периода. Тогда значения этих расходов можно представить с учетом заданного темпа инфляции так, как показано в табл. 5.1.

Таблица 5.1

Условно-постоянные расходы по проекту, млн руб.

Определим распределения значений рисковой прибыли по данной инвестиции для каждого года в течение четырехлетнего периода исполнения проекта. В соответствии с исходными данными можно записать: S = 80; X = 70; а = 1,3; b = 0,9; г = 15%; i = 10%.

Определим прибыль в первом году, используя формулы, представленные на рис. 5.1, в каждом из двух состояний экономики. Если прибыль возрастала с темпом роста а, то получим:

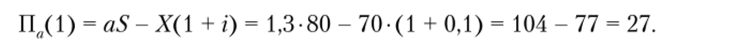
Во втором состоянии экономики в первый год будем иметь:

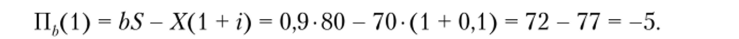
Для второго года поток рисковой прибыли определим в соответствии с формулами, которые показаны на рис. 5.2:

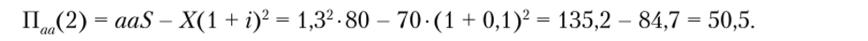
Аналогично могут быть рассчитаны остальные значения прибыли во втором году. Их оставляем для самостоятельных расчетов (см. практическое задание 1).

Расчеты прибыли третьего года проводятся в соответствии с формулами, представленными на рис. 5.3. Например, в том случае, когда доход возрастал каждый год с темпом роста, равным а, получим:

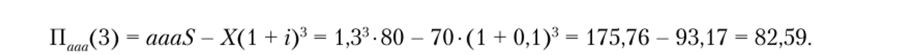
В том случае, когда каждый год в течение трех рассматриваемых лет доход возрастал с темпом роста, равным 6, имеем:

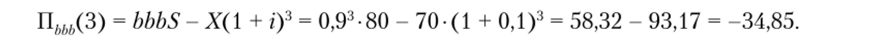
Так же определяются значения доходов во всех остальных случаях для третьего года. В табл. 5.2 приведено распределение рисковой прибыли третьего года.

Расчеты доходов четвертого года проводятся по формулам, аналогичным приведенным на рис. 5.3, с той разницей, что результаты относятся к четвертому году. Следует учитывать, что базовая условная прибыль изменяется в данном случае по-прежнему в соответствии с коэффициентами а и b соответственно. Объем условно-постоянных расходов изменяется, как и ранее, согласно темпам роста инфляции. Например, для случая, когда базовая прибыль изменялась с темпом роста а, в течение четырех лет имеем:

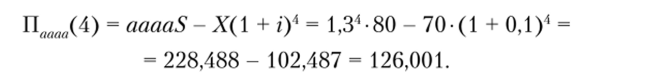
Если в начале базовый условный доход возрастал в течение двух лет с темпом роста а, а затем два года с темпом роста b, то в конце четвертого года доход составит:

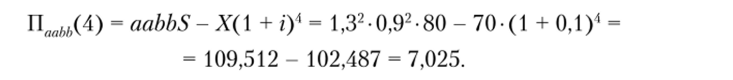
Аналогично можно определить объем прибыли четвертого года в том случае, когда цена менялась только с темпом роста Ь. Используя исходные данные, получим:

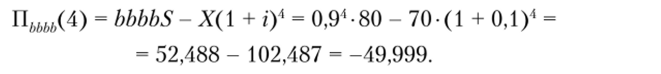
Подобным образом рассчитываются значения прибыли для четвертого года при других сочетаниях темпов роста базовой части прибыли. Все остальные значения прибыли для каждого периода оставляем для самостоятельных расчетов (см. практическое задание 1).

Очевидно, что число конкретных значений прибыли для каждого периода меньше общего числа учитываемых исходов для каждого периода. Это обусловливается тем, что число конкретных значений прибыли определяется числом сочетаний рассматриваемых темпов роста. Выше это показано для случая трех лет. Для четвертого года можно выделить пять значений коэффициента т и соответствующих им сочетаний темпов роста базовой условной прибыли: т = 4, аааа т = 3, аааЬ; т = 2, aabb т = 1, abbb т = 0, bbbb. В приведенных выше обозначениях прибыли четвертого года для наглядности используется сочетание темпов роста, а не параметр т. Все это приводит к резкому сокращению конкретных значений расчетной прибыли за каждый год, которые для данного примера представлены на рис. 5.4. Как было отмечено выше, существенное отличие доходов по рыночному опциону от доходов реального бизнеса в условиях аналогичного дерева событий.

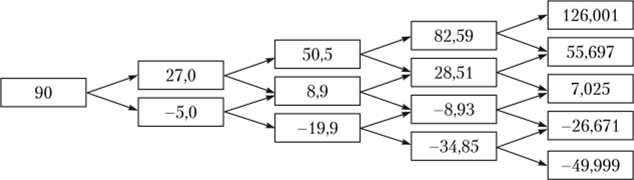
Рис. 5.4. Расчетные значения прибыли за каждый год, млн руб.

определяется наличием одного дохода, который может принимать отрицательное значение.

Полностью распределение рисковой прибыли в условиях рассматриваемого дерева событий, которое предполагает только два исхода из каждого узла и строится для четырех рассматриваемых периодов, приведено в табл. 5.2. Очевидно, что на схеме, показанной на рис. 5.4, приведены все возможные конкретные числовые значения прибыли за каждый рассматриваемый год. Следует только иметь в виду, что общее число возможных исходов за год t сос тавляет 2'.

Таблица 5.2

Распределение рисковой прибыли каждого года, млн руб.

Указанная выше схема расчетов будущей прибыли или иной формы доходов предусматривает возможности получения отрицательных значений, что требует определенной адаптации к условиям реального бизнеса, которую можно рассмотреть с двух точек зрения. Во-первых, можно предположить, что при условии отрицательного размера прибыли фирма имеет резервы капитала для финансирования продолжения проекта и покрытия убытков, т. е. она может реализовать данный проект даже при определенных убытках в некоторые периоды. Формально это означает, что расчеты производятся в соответствии с данными табл. 5.2. Это даст возможность оценить рассматриваемую инвестицию с точки зрения полученного распределения прибыли за каждый год, которое обеспечивает исполнение данного инвестиционного проекта.

Во-вторых, при наличии отрицательных значений прибыли можно рассмотреть возможности управления рисками в процессе реализации данной инвестиции, например, в случае отрицательной прибыли провести диверсификацию бизнеса или использовать реальные опционы на продажу бизнеса или его приостановку. Это позволит существенно повысить текущую ценность будущей рисковой прибыли анализируемого проекта.

Предполагая возможности получения отрицательной прибыли, проведем расчеты текущей стоимости распределения прибыли каждого года, используя простую однопериодную биномиальную модель [см. формулу (5.8)]. Будем интерпретировать распределение прибыли каждого года как распределение дохода по многопериодному опциону со сроком исполнения один, два, три или четыре года соответственно. Определим стоимость каждого такого опциона на покупку, используя простую биномиальную модель оценки стоимости опциона со сроком исполнения, равным одному году.

Для этого вначале определим значения величии q и 1 — q, которые сохраняются постоянными для всех рассматриваемых периодов и рассчитываются по формуле (3.9):

Тогда текущую стоимость прибыли первого периода по формуле оценки стоимости опциона на покупку со сроком исполнения один период (5.1) можно, учитывая два ее значения из табл. 5.2, определить так:

Полученное значение характеризует настоящую стоимость рисковой прибыли первого года, но рассматриваемому проекту.

При анализе прибыли второго года обратим внимание на то, что в условиях биномиальной модели возникает четыре значения дохода, которые можно объединить в пары в зависимости от того, какое значение темпа роста базового дохода было достигнуто на предыдущем (первом) периоде (см. табл. 5.2). Для каждой пары таких доходов определим их стоимость в нервом периоде, используя формулу оценки опционов на покупку со сроком исполнения один период вида (5.2) и (5.3).

Тогда для первой пары, но формуле (5.2) получим: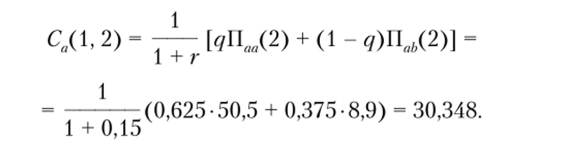

Аналогично для второй пары значений оценка прибыли второго года на первый период по формуле (5.3) составит:

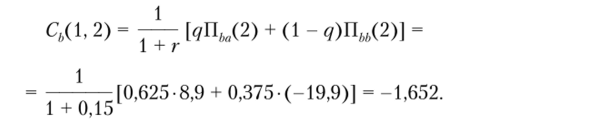
Полученные значения представляют собой расчетные оценки стоимости прибыли второго года в первом году. Рассмотрим эти значения как доходы по опциону па покупку со сроком исполнения один период и определим стоимость этих доходов в нулевом или начальном периоде. Тогда, учитывая формулу (5.4), получим:

Величина С (2) характеризует оценку стоимости ожидаемой рисковой прибыли второго года в нулевом году. Аналогичным путем, используя формулу определения стоимости опциона на покупку со сроком исполнения один период, можно пересчитать доходы третьего года в оценку соответственно второго, первого и нулевого годов, а доходы четвертого года — в оценку третьего, второго первого и нулевого годов. При этом по-прежнему используем формулу оценки стоимости опциона со сроком исполнения, равным одному периоду вида (5.8).

Например, для первой пары прибыли третьего года получим:

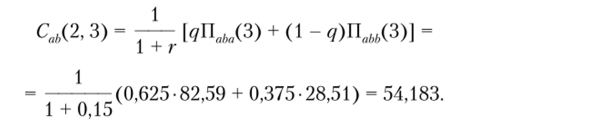
Для последней пары распределения прибыли третьего года имеем:

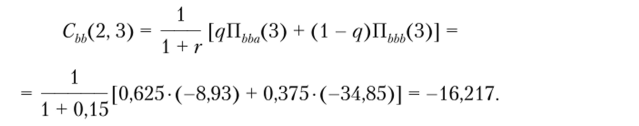
Аналогичные расчеты выполнены последовательно для каждой пары из распределения прибыли рассматриваемого периода. В последнем случае получаем текущую оценку распределения прибыли третьего года на нулевой год:

Полностью результаты расчетов настоящей стоимости рисковой прибыли третьего года приведены в табл. 5.3. Там же показана последовательность получаемых промежуточных оценок доходов третьего года.

Таблица 53

Определение настоящей стоимости распределения прибыли третьего года, млн руб.

Полученная оценка текущей стоимости распределения прибыли третьего года с учетом ее отрицательных значений в третьем году С (3) = 18,739 млн руб.

Аналогично можно проанализировать распределение четвертого года, принимая во внимание имеющиеся отрицательные оценки значения прибыли четвертого года. Так, для последней пары значений прибыли, приведенной в четвертом столбце табл. 5.2, получим:

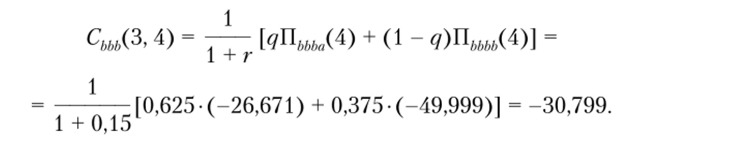
Рассматриваемая пара значений прибыли четвертого года имеет в третьем году отрицательную оценку.

При этом оценку в третьем году первой пары значений распределения прибыли четвертого года можно определить так:

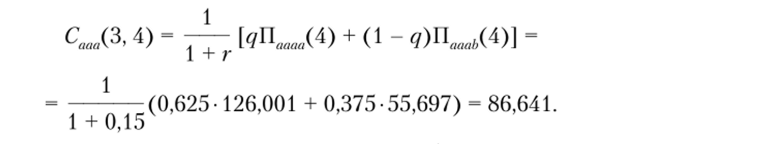
Для второй пары значений распределения прибыли четвертого года соответственно получим: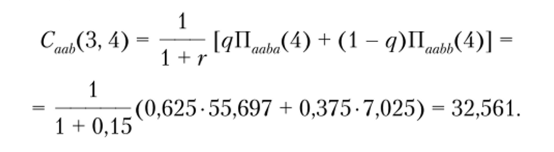

Аналогично можно построить все промежуточные оценки распределения прибыли четвертого года. Их значения приведены в табл. 5.4. Их также оставляем для самостоятельных расчетов (см. практическое задание 1).

Таблица 5.4

Определение настоящей стоимости прибыли четвертого года, млн руб.

Окончательную оценку текущей стоимости распределения прибыли четвертого года можно получить, используя оценки распределения прибыли четвертого года на первый год. Используя формулу (5.8), имеем:

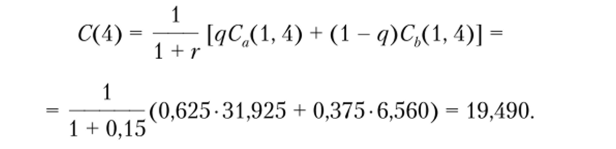
Текущая оценка распределения прибыли четвертого года составляет С (4) = 19,490 млн руб.

Используя полученные результаты, можно найти окончательную оценку всего рассматриваемого распределения прибыли за каждый год. Общая предельная стоимость рассматриваемой рисковой прибыли данной инвестиции, млн руб., определяется по формуле (5.9) как сумма оценок текущей стоимости рисковой прибыли за каждый год в течение периода исполнения проекта:

С4) = С ( 1) + С ( 2) + С (3) + С (4) = 13,043 + 15,955 + 18,739 + 19,490 = 67,227.

Учитывая полученный результат, можно сделать два принципиальных вывода.

Во-первых, сумму 67,23 млн руб. можно проинтерпретировать как текущую оценку стоимости рискового бизнеса или соответствующих активов капитала, порождающих рисковые потоки прибыли, которые были учтены при получении соответствующих расчетных оценок.

Во-вторых, в условиях данного примера, если его данные рассматривать как инвестиционный проект, то не выгодно платить за данную инвестицию, или, что-то же самое, инвестировать в данный проект, более 67,3 млн руб. Если учесть, что по условию данного примера инвестиционные расходы по проекту составляют 60 млн руб., то результаты приведенных расчетов показывают, что рассматриваемый проект целесообразно осуществить. В противном случае следовало бы либо отказаться от исполнения данного проекта и проанализировать другие возможности развития бизнеса, позволяющие сократить инвестиционные расходы или условно-постоянные расходы, либо использовать какие-либо методы управления рисками.

С точки зрения практической реализации рассматриваемого проекта необходимо проанализировать возможности развития бизнеса в случае, если возникает исход с отрицательной прибылью. По данным табл. 5.2 отрицательный исход возникает уже в первый год. Можно показать, что прекращение бизнеса в конце первого года приводит к существенному ухудшению значения текущей стоимости будущего распределения прибыли. Возможности использования управления рисками для снижения отрицательной прибыли и улучшения рассматриваемого проекта оставляем для самостоятельного анализа (см. практическое задание 2). Если убытки в 5 млн руб. для фирмы не являются критичными и она может их покрыть резервами капитала, то рассмотрим прекращение бизнеса во втором году, если развитие пойдет, но неблагоприятному варианту дерева событий. Тогда проанализируем следующее распределение прибыли, которое возникает в том случае, если прекращается исполнение проекта при ожидаемых убытках во втором году. Это распределение прибыли можно записать так, как показано в табл. 5.5. Аналогично предыдущему выполним расчеты текущей стои;

Таблица 5.5.

Распределение рисковой прибыли каждого года, млн руб.

мости распределений прибыли. Очевидно, что оценка распределения прибыли первого года не изменяется и составит С (1) = 13,043.

При определении текущей оценки распределения прибыли второго года оценка первой пары значений второго года в первом году составит, как и ранее, С"(1, 2) = 30,348.

Аналогично для второй пары значений прибыли, учитывая нулевое значение прибыли, получим:

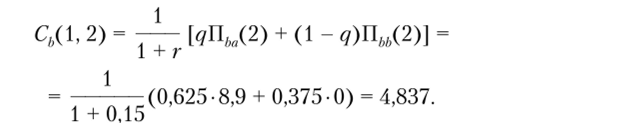
Значение текущей стоимости распределения прибыли второго года составит:

При расчетах текущей стоимости распределения прибыли третьего года следует учитывать, что последняя пара значений распределения прибыли данного года принимается равной нулю.

Это меняет значение оценки четвертой пары значений прибыли третьего года во втором году и, соответственно, оценку этой части распределения прибыли третьего года в первый год:

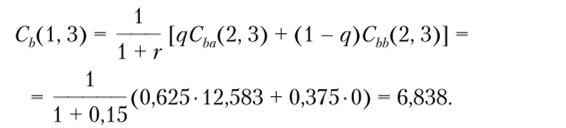
Аналогичные расчеты выполнены последовательно для каждой нары из распределения прибыли рассматриваемого периода. В последнем случае получаем текущую оценку распределения прибыли третьего года на нулевой год:

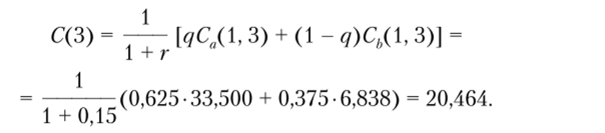
При анализе распределения прибыли четвертого года учтем, что последние четыре значения распределения становятся равными нулю. Это приведет к изменению промежуточной оценки первого года по отношению к оценке второго года. Тогда получим:

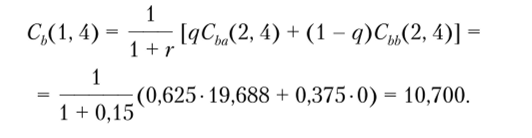
Это приводит к изменению окончательной оценки текущей стоимости распределения прибыли четвертого года. Ее можно определить, учитывая, что значение второй оценки распределения прибыли четвертого года на первый год остается неизменным. Используя формулу (5.4), имеем:

Текущая оценка распределения прибыли четвертого года составляет С (4) = 20,84 млн руб.

Используя полученные результаты, можно определить окончательную оценку всего рассматриваемого распределения прибыли за каждый год. Общую предельную стоимость рассматриваемой рисковой прибыли данной инвестиции, млн руб., с учетом прекращения проекта во втором году при условии наступления неблагоприятного события рассчитаем, используя формулу (5.9), как сумму полученных оценок текущей стоимости распределений рисковой прибыли за каждый год в течение периода исполнения проекта: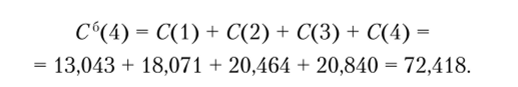

Очевидно, прекращение проекта во втором году при условии выхода на неблагоприятную ветку дерева событий привело к росту значения текущей стоимости рассматриваемой рисковой прибыли. Этот прирост также можно проинтерпретировать как предельную стоимость реального опциона на прекращение проекта при условии наступления неблагоприятного события во втором году.

Представленные в данной главе методы обоснования многопериодных рисковых инвестиций показывают, что для оценки подобных инвестиций или определения стоимости рисковых активов капитала можно использовать подход, основанный на формировании эквивалентных портфелей и применении биномиальной модели. Основное преимущество состоит в том, что соответствующий ответ может быть получен без учета вероятностей наступления будущих состояний экономики. Однако использование этого метода предполагает, что могут быть сформированы, или хотя бы определены, эквивалентные портфели активов, которые приносят в каждом рассматриваемом периоде такие же рисковые доходы, которые обеспечивает анализируемый инвестиционный проект или рассматриваемые материальные активы капитала.