Многопериодная биномиальная модель равновесной цены рыночного опциона

Кратко рассмотрим возможности использования многопериодной биномиальной модели в условиях реального бизнеса для обоснования его текущей стоимости и оценки рисковых инвестиций. Основная особенность развития реального бизнеса состоит в том, что доходы по бизнесу возникают каждый рассматриваемый период, в то время как по опциону европейского типа доходы возникают или не возникают только в конце периода исполнения опциона.

Существенное отличие потока доходов по опциону от тех или иных доходов в сфере реального бизнеса заключается в том, что при оценке доходов по опциону на продажу доход либо положителен при исполнении опциона, либо равен нулю при неисполнении опциона. В условиях же реального бизнеса возможно получение отрицательного или нулевого дохода, но при этом встает вопрос о том, можно ли продолжать бизнес в случае возникновения отрицательного дохода либо убытков или нельзя. Либо собственник располагает достаточным резервным капиталом, чтобы компенсировать убытки, и возможно дальнейшее развитие даже при отрицательных доходах. Либо при наличии отрицательных доходов необходимо рассмотреть возможности управления рисками, позволяющие не допускать их падения ниже определенного уровня.

Проведем вначале анализ доходов рыночного опциона на покупку при условии, что период исполнения этого опциона больше одного периода, а далее обратим внимание на особенности определения доходов и постановку многопериодной биномиальной модели в условиях реального бизнеса.

Будем считать, что выполняются следующие исходные предпосылки:

• 1) рассматриваемый период исполнения проекта разбивается на t подпериодов; t = 0, 1,…, Г;
• 2) в каждый подпериод выделяются только два будущих состояния экономики, в одном из которых цена базового актива либо возрастает с постоянным темпом роста а, либо изменяется с темпом роста Ъ
• 3) при оценке распределения доходов периода ?, t = 1, …, Г, не учитываются доходы предыдущих периодов;
• 4) в каждый период предполагается возможность формирования эквивалентных портфелей из рискового и безрискового активов, которые приносят такие же доходы, что и рассматриваемый опцион.

Сохраним введенные выше обозначения и будем считать, что р₀ — текущая цена базового актива; р_к — цена исполнения по опциону; г — безрисковая ставка процента. При этом, как отмечено выше, b < 1 + г < а. В этих условиях стоимость опциона на покупку существенно зависит от темпов роста цены в каждом из двух возможных состояний экономики. Обозначим доход по опциону в первом периоде при условии реализации первого состояния экономики следующим образом:

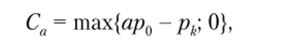
а при наступлении второго будущего состояния.

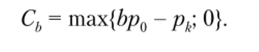
С учетом этих обозначений формулу для определения стоимости опциона со сроком исполнения, равным одному периоду, учитывая (3.8) можно записать так:

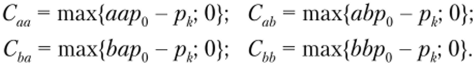
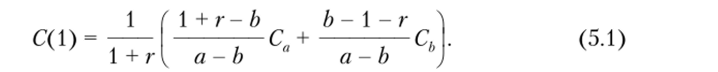
При анализе опциона со сроком исполнения два периода обозначим его доходы во втором году в зависимости от темпов роста цены базового актива:

Тогда оценку первой пары доходов второго периода на первый период, учитывая рост цены базового актива в первом периоде с темпом а и используя формулу (5.1), можно записать так:

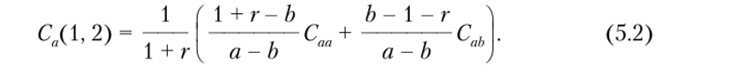
Для второй пары доходов при условии, что цена базового актива в первом периоде возрастала с темпом роста &, аналогично получим:

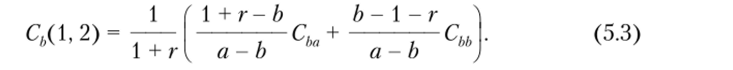
Для того чтобы оценить стоимость доходов второго периода на нулевой период представим себе опцион с доходами, определяемыми по формулам (5.2) и (5.3). Тогда для оценки стоимости этих доходов в нулевом периоде можно воспользоваться формулой оценки стоимости опциона со сроком исполнения один период (5.1), которая принимает вид.

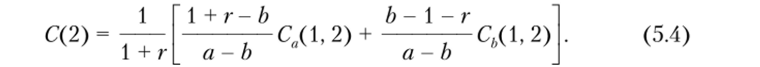
Формула (5.4) позволяет определить стоимость опциона со сроком исполнения два периода через стоимости опционов со сроком исполнения один период.

Можно воспользоваться этим подходом в более общем виде. Будем считать, что определены рисковые доходы по опциону со сроком исполнения в периоде ?, которые зависят от значения параметра т в следующей форме:

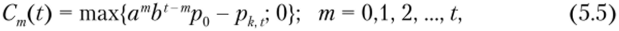
где т показывает, сколько раз в течение периода t цена возрастала с темпом роста а; соответственно, t — т показывает, сколько раз за этот период цена возрастала с темпом роста b p_{k t} — цена исполнения в периоде t.

Рассмотрим опцион со сроком исполнения в следующем периоде t + 1. Если предположить, что в периоде t достигнуто состояние экономики, характеризующееся определенным значением параметра т и доходом C_m(t)> который определяется по формуле (5.5), то в следующем периоде t+ 1 может быть получен в зависимости от темпов роста цены базового актива один из двух доходов, которые рассчитываются следующим образом:

Формула (5.6) показывает доход по опциону в том случае, если цена базового актива в периоде t + 1 возрастала с темном роста а; соотношение (5.7) — то же самое, но в случае, когда эта цена возрастала с темпом роста Ь.

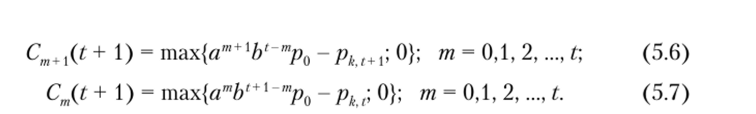
Зафиксируем определенное значение параметра т и некоторый уровень дохода C_m(t) в одном из узлов дерева событий и определим соответствующую им пару доходов периода t + 1 по формулам (5.6) и (5.7). Применяя формулу вида (3.8) к этой паре доходов, получим оценку этих доходов периода t + 1 на период t в зависимости от значения параметра т:

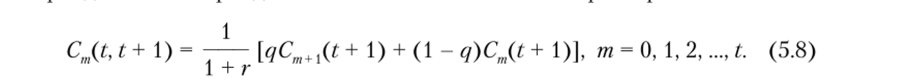
Перебирая значения параметра т и используя формулы (5.6) и (5.7), можно построить полное распределение доходов для опциона со сроком исполнения в конце периода t + 1. Применяя формулу (5.8) последовательно для каждой пары доходов этого распределения, можно пересчитать распределение доходов периода t + 1 в оценки на период ?, используя формулу (5.8). Поскольку расчеты осуществляются отдельно, то применение формулы вида (5.8) для получения оценки доходов одного периода на ближайший к нему возможно даже в том случае, когда коэффициенты а и Ь, а также ставка процента г меняются от периода к периоду. При этом соответственно изменяются параметры формул (5.6) и (5.7), используемые для расчета доходов каждого периода. Продолжая дальше этот процесс и учитывая полученные на каждом шаге результаты расчетов по указанным формулам, в конечном итоге будем иметь оценку рисковых доходов периода t на нулевой или начальный период. Обозначим ее C (t). Тогда текущая стоимость портфеля опционов с рассматриваемым дискретным распределением рисковых доходов за каждый подпериод в течение периода Г, определяемая по биномиальной модели С⁽Т), составит:

При анализе результатов практических расчетов многократное применение простой однопериодной биномиальной формулы вида (5.8) для различных периодов позволяет понять, как меняются при этом оценки некоторого распределения от периода к периоду. Подобные расчеты также дают возможность использовать переменные темпы роста стоимости базового актива. Это может быть полезно в процессе оценки доходов бизнеса в реальном секторе экономики.

Второй, более общий, подход к оценке рыночного опциона с длительным периодом исполнения связан с использованием известной формулы, предложенной в 1979 г. Дж. Коксом, С. Россом и М. Рубинштейном для определения цены опциона на покупку с периодом до исполнения, равным t. Ее использование предполагает постоянные темпы роста цены базового актива каждый период. В общем виде ее можно записать так: где т— число раз, когда цена возрастала с темпом роста а; соответственно, t-m — число раз, когда цена возрастала с темпом роста Ь остальные обозначения сохранены.

Формула (5.10) верна только при условии, что выбрано такое наименьшее целое т, что рыночная цена базового актива опциона в период t будет больше, чем цена исполнения по опциону. Формально это означает, что.

Выполнение условия (5.11) означает, что опцион на покупку будет исполнен в конце периода t. Тогда это означает, что.

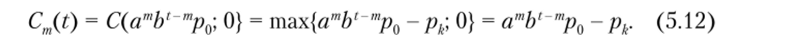
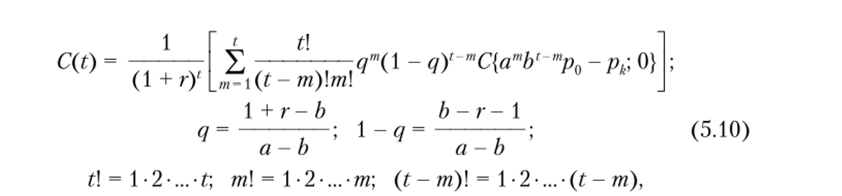
Формула Кокса —Росса—Рубинштейна (5.10) показывает, что стоимость опциона за t периодов до исполнения также не зависит от вероятностей наступления выделенных будущих состояний экономики, а определяется только в зависимости от ожидаемых значений цены базового актива — предмета опциона — в каждый будущий период^[1].

Следует отметить, что возможности применения этой формулы существенно зависят от разбиения рассматриваемого периода до исполнения опциона на соответствующие подпериоды. Эти подпериоды должны быть относительно малы, в противном случае формула (5.10) даст довольно грубые приближенные оценки.

Основная проблема применения полученных формул для оценки текущей стоимости рисковых доходов бизнеса или конкретных реальных инвестиций связана с оценкой темпов роста цены базового актива а и /?, поскольку сам производимый продукт, как и продукты-аналоги, может отсутствовать на рынке, а следовательно, и каких-либо рыночных оценок указанных параметров просто не существует. В этом случае речь может идти об оценке и учете субъективных ожиданий. При этом чем больше длительность рассматриваемого периода, тем менее содержательной представляется оценка этих ожиданий. С точки зрения оценки устойчивости полученного решения могут быть полезны имитационные расчеты.

• [1] Доказательство формулы Кокса, Росса и Рубинштейна см., например, в кн.: Мельников А. В., Волков С. Нечаев М. Л. Математика финансовых обязательств. М.: Изд-во ГУ ВШЭ, 2001.С. 54−57.