Математика Л. Эйлера

К 1730—1740-м гг. в интегральном и дифференциальном исчислении сложилась очень сложная ситуация. Наверно, первый раз за свою историю, за исключением легендарного пифагорейского кризиса, математика оказалась в действительно кризисной ситуации. Все рассуждения о ясности и отчетливости математических истин уже никого не убеждали. Пришедшая на смену декартовскому жесткому эфиру модель упругого эфира оказалась весьма проблемной. Математики не смогли описать новые траектории, которые предлагал упругий эфир.

Математический анализ эфирной традиции стал сильно пробуксовывать и терять авторитет. Еще в 1708 г. Лейбниц провидчески предупреждал: «Нс следует удивляться, что анализ бесконечно малых делает только первые шаги и что мы совсем не хозяева положения ни в квадратурах, ни еще менее в обратной задаче касательных и в еще меньшей мере при решении дифференциальных уравнений»^[1]. И это заявление прозвучало после всех тех успехов, которые были описаны в предыдущих двух параграфах.

Критика новой концепции упругого эфира и математического анализа эфирной традиции развернулась с двух сторон. Сначала расскажем об атомистах. Еще со времен Галилея атомисты претендовали на духовную гегемонию в европейской культуре, но Декарт рассеял эти надежды. В конце XVII в. атомисту Ньютону приходилось преподавать картезианство в Кембридже.

Но во многом благодаря внутренней революции в стане сторонников эфира ситуация стала меняться. Последователи Лейбница, в первую очередь Лопиталь и Вариньон, серьезно пошатнули позиции картезианцев в Парижской академии наук. Физические воззрения Лейбница (спор о живой силе и законах механики) практически похоронили картезианскую физику. Но в то же время Лейбниц и его последователи не успели к 1730-м гг. создать достойную замену картезианской физике.

В математике Лейбниц постоянно колебался в вопросах о статусе бесконечно малых и в принципе по вопросам обоснования анализа. Этим и воспользовались ныотонианцы. В первой половине XVIII в. они полностью вытеснили картезианство из Англии. Вольтер так характеризовал сложившуюся ситуацию в естествознании этого периода: «Француз, приехавший в Лондон, оставил мир полным, а находит его пустым. В Париже видят Вселенную состоящей из вихрей тонкой материи, в Лондоне ничего подобного не находят. У нас причина приливов — давление Луны, а у англичан, наоборот, море тяготеет к Луне; поэтому когда вы ждете, что Луна должна вызвать прилив, те господа ожидают отлив… У вас, картезианцев, все производится натиском, что едва ли понятно, у господина Ньютона — притяжением, причина которого столь же не ясна. В Париже вы представляете Землю в форме дыни, в Лондоне она сплющена с двух сторон. Для картезианцев свет существует в воздухе, для ньютонианца он приходит от Солнца в шесть с половиной минут. Ваша химия оперирует кислотами, щелочами и тонкой материей, тяготение господствует вплоть до английской химии»^[2].

Более того, трудами самого Вольтера ньютонианство начинает проникать и на континент. Здесь также следует упомянуть спор о приоритете между Ньютоном и Лейбницем, который, очевидно, закончился явной победой последователей Ньютона. В этот же период Тейлор и Маклореи дают новые очень эффективные математические инструменты для разложения функций в ряды, именно исходя из атомистических представлений. В целом ситуация явно складывалась не в пользу последователей эфира.

С другой стороны, против Лейбница и его школы выступили и сторонники эфирных концепций. Так или иначе они стояли на позициях, более близких к Декарту, чем к Лейбницу. Критика была развернута как раз против модели упругого эфира и математического анализа школы Лейбница. Самым известным критиком с этих позиций оказался философ Д. Беркли.

В 1734 г. Беркли выпустил книгу «Аналитик», которая вызвала эффект разорвавшейся бомбы. Вот как Ж. Бюффон охарактеризовал сложившуюся тогда ситуацию: «Все было спокойно в течение нескольких лет, как вдруг в самой Англии появился доктор, враг науки, объявивший войну математикам… И он заявляет нам, что исчисление бесконечного ошибочно, ложно, подозрительно неясно, что принципы его недостоверны и что оно приводит к цели лишь случайным образом»^[3].

Книга содержала как критику атомизма, так и критику лейбницевского математического анализа. Основной удар критики был направлен на понятие бесконечно малой величины: «Это ни конечные величины, ни бесконечно малые, ни даже ничто. Не могли ли бы мы их назвать призраками почивших величин?»^[4] Основной вопрос стоял о том, можно ли отбрасывать бесконечно малые более высоких порядков без ущерба для точности. Ведь, согласно Лейбницу и Ньютону, (а + а)^[4] = а^[4] + 2аа + а^[4] и а^[4] можно отбросить. Получалось, что одно из классических разложений математики (а + b)² = а^[4] + 2ab + Ь² здесь просто не действовало.

Но тем не менее результаты, как выше было показано на примере с решениями Гюйгенса, который работал старыми методами, и Лейбница, который работал новыми методами, совпадали. Беркли объяснил эго компенсацией ошибок. Сначала делается одна ошибка, когда кривая линия заменяется прямой при спрямлении, а затем эта ошибка компенсируется при отбрасывании бесконечно малых. Это объяснение стало весьма популярно и среди математиков. В целом критика Беркли привела к появлению агностицизма и антиномий Канта. В антиномиях как раз и рассматриваются две физико-математические системы: атомизм и эфирная концепция. Кант утверждает, что обе они одинаково истинны, поэтому разум не может сделать выбор и так осознает свои границы.

Вот в такой ситуации оказалась эфирная традиция к 1730—1740-м гг. Вопрос встал о выживании. И тут явился молодой швейцарец, который вдохнул новую жизнь в увядающую традицию. Этот молодой гений был Л. Эйлер. Именно ему было суждено вывести эфирную традицию из кризиса, и именно поэтому его значение в математике столь велико. Его работы стати знаковыми для своей эпохи. Его трудами эфирная концепция наконец смогла снова одолеть атомизм и добиться гегемонии в европейской культуре второй половины XVIII — первой половины XIX в.

Лейбниц и его последователи только начали строительство математического и физического аппарата новой модели эфира. К моменту появления Эйлера эта работа была еще далека до завершения. Более того, совсем не было очевидно, что эта работа в принципе может быть успешно выполнена. Суть проблемы заключалась в том, что новый эфир породил множество траекторий, которые не слишком хотели описываться математически. В первую очередь, речь шла о различных колебательных процессах. И в описании этих процессов возникла очень серьезная конкуренция с атомизмом.

Атомизм всегда использовал идею бесконечного, поэтому явно предпочитал различного рода бесконечные ряды. Эфирная традиция стремилась дать конечные квадратуры в максимально широком классе функций. Поэтому надо было отделить то, чтобы было возможно квадрировать в конечном виде, от того, что не удавалась так квадрировать. Эйлер, Даламбер, Лагранж как раз и начали решение этой задачи.

Принципиально было ясно, что всякая функция раскладывается в бесконечный ряд. Эйлер писал: «Не будет никакого сомнения в том, что всякая функция может быть преобразована в такое бесконечное выражение Az^a + Bz$ + Cz'< + Dz^b +где показатели а, (3, у, 5 и т. д. обозначают любые числа»^[10]. Понятно, что последователям эфирной традиции приходится с этим смириться и также использовать бесконечные ряды, и в первую очередь степенные ряды. Эйлер опирается на разложения элементарных трансцендентных функций в бесконечные ряды:

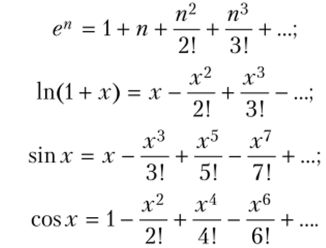
Но тут постепенно выясняется, что бесконечные степенные ряды не так уж и всесильны. Так, Эйлеру были известны функции, которые выражаются одной формулой, но не представимы степенным рядом. В 1748 г. он рассмотрел функцию у = (-l) —^v, график которой состоит из бесчисленного множества точек, лежащих всюду плотно на прямых у = -1 и у = 1, но, как он выражался, нигде не смежных (функция принимает действительные значения только при значениях х, равных несократимой дроби с нечетным знаменателем)^[11]. И такие парадоксальные функции уже начали беспокоить математиков.

Таким образом, разрывные функции стали постепенно входить в круг интересов математиков. Они стали аргументом против эфирной математики. Традиция материального эфира пыталась некоторое время игнорировать наличие разрывных функций. Правда, эта ситуация продолжалась недолго. «Но с особенной ясностью необходимость в разрывных функциях обнаружилась при исследовании задачи о малых плоских колебаниях струны, которой Эйлер, вслед за Даламбером, занялся в конце 1740-х.

()^[11] ь/ с)^[11] if.

годов. Задача выражается уравнением —f- = а^[11]—общее решение кото-

at^[11] ах^[10]

рого Даламбер получил в виде суммы произвольных функций у = /_{(х + + at) + f₂(x — at)"^x.

В 1770 г. Эйлер пишет: «В го время как прежде рассмотренные интеграции давали только непрерывные функции, в данном случае в анализе появляются также и разрывные функции, что до сих пор многим видным математикам представляется противоречащим его принципам. Особенная сила интеграций, рассматриваемых в этой книге, в том и состоит, что при них могут встречаться и разрывные функции; так что надо полагать, что благодаря этому существенно новому исчислению границы анализа значительно расширяются»^[17][18].

Эфирная математика смогла вплести разрывные функции в свое исчисление. Однако в первой половине XIX в. атомист Фурье дал решение для разрывных функций в виде тригонометрического ряда. Этот ряд оказался более мощным оружием, чем методы эфирной традиции. Но это будет много позже периода деятельности Эйлера.

Эйлер, очевидно, исходил из метода касательных Лейбница. Метод касательных основывался на рассмотрении отношений dy/dx в случае, когда они становятся бесконечно малыми. Поэтому для Эйлера дифференциальное исчисление определяется как «метод определения отношения исчезающих приращений, получаемых какими-либо функциями, когда переменному количеству, функциями которого они являются, дается исчезающее приращение»^[19].

Более того, Эйлер определяет производную, играющую главную роль в методе касательных, через предел этих исчезающих количеств. При этом приращения «становятся все меньшими и меньшими, и тогда мы найдем, что их отношение все более и более приближается к некоторому определенному пределу, которого они достигают, однако, лишь тогда, когда полностью обращаются в нуль»^[20].

Здесь вполне хорошо видно влияние одной из метафизических концепций обоснования бесконечно малых, данных в свое время Лейбницем. Речь идет об исчислении нулей. Метод касательных однозначно ведет к составлению дифференциальных уравнений. Поэтому вся задача математического анализа будет состоять в решении этих дифференциальных уравнений в конечном или в бесконечном виде.

К середине XVIII в. уже стало понятно, что дифференциальные уравнения весьма разнообразны, но виду. Основное разделение дифференциальных уравнений состояло в выделении обыкновенных дифференциальных уравнений и уравнений в частных производных. В свою очередь обыкновенные дифференциальные уравнения делятся на линейные и нелинейные. Теория решения нелинейных дифференциальных уравнений была построена исторически ранее теории решения линейных дифференциальных уравнений.

Как только математики эфирной традиции начали строить свои механическую концепцию движения, им сразу пришлось даже в самых простейших случаях столкнуться с нелинейными дифференциальными уравнениями второго порядка. «Динамическое уравнение Эйлера, определяющее движение абсолютно твердого тела, имеющего неподвижную точку, представляет нелинейную систему трех уравнений второго порядка (относительно эйлеровских углов |/, 0, (р как функции времени t)»¹.

Вообще, решение задач динамики и статики со сложными связями приводило к необходимости решать нелинейные дифференциальные уравнения. Естественно, что последователи Лейбница обязаны были попробовать решить эти уравнения в конечном виде. С этой целью они стали использовать метод интегрирующего множителя, о котором уже говорилось в предыдущем параграфе. Этот метод полностью соответствовал традиции Аполлония и Диофанта, ибо преобразовывал исходную кривую в пересечение двух более простых по порядку кривых.

Метод интегрирующего множителя должен был заменить ранее применявшийся и не всегда эффективный метод разделения переменных. «Многие строят весь фундамент решения дифференциальных уравнений на разделении переменных… Желателен метод, посредством которого отыскивается требуемая подстановка; однако мы не обладаем уверенными правилами, так как подобные подстановки не основываются на определенном принципе. Поэтому разделение переменных не следует рассматривать как истинный фундамент решений дифференциальных уравнений, особенно потому, что для уравнений второго и высшего порядка оно не применимо»².

Теперь более подробно рассмотрим, как метод интегрирующего множителя использовался при решении нелинейных дифференциальных уравнений. Эйлеру пришлось одному из первых начать строительство динамики механического эфира.

Огромное количество задач динамики эфира сводилось к решениям нелинейных дифференциальных уравнений второго порядка. Поэтому умение решать такие уравнения оказалось весьма необходимым. Эйлер выбрал в качестве основного пути решения таких уравнений метод понижения порядка дифференциального уравнения. Это было связано с тем, что многие уравнения первого порядка уже умели решать, поэтому сведение дифференциальных уравнений второго порядка к уравнениям первого порядка было бы очень эффективным средством решения. Но не все нелинейные дифференциальные уравнения второго порядка оказалось возможным свести таким образом.

Эйлер сумел выделить четыре вида уравнений второго порядка, допускающих сведение к уравнениям первого порядка. Такое сведение осуществлялось с помощью замены независимой переменной и неизвестной функции. В качестве примера можно привести уравнение.

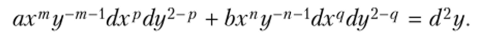
История математики с древнейших времен до начала XIX века. Т. 3. С. 372.

Эйлер решил это уравнение с помощью подстановок у = e^vn у = еЧ, где t — некоторая новая независимая переменная. В данном случае Эйлер продолжил традицию использования экспоненциальной подстановки, идущей от Иоганна и Николая II Бернулли. Следует еще дополнительно отметить появление при решении данного уравнения понятия однородности.

Эйлер считал х, у, clx, dy, сР-у однородными в случае, если они будут все иметь одно и то же измерение.

Но понятие однородности оказалось не слишком понятным для современных Эйлеру математиков. Даваемые Эйлером разъяснения не очень помогли делу. Поэтому в более поздних исследованиях Эйлер немного иначе трактовал понятие однородности. Сначала он превращал нелинейное дифференциальное уравнение второго порядка в систему двух уравнений первого порядка. Тогда «с помощью соотношений dy = pdx, dp = qdx формулируется следующий критерий однородности: переменные х_у у, р, q должны входить в уравнение так, чтобы подстановки уих, q = v/x исключали из уравнения х»^[21].

Понятие однородности Эйлер вычитал у Диофанта. Так, известный исследователь Диофанта И. Г. Башмакова использует это понятие однородности для объяснения основных методов решения неопределенных уравнений, применяемых Диофантом. Кроме того, известно, что именно Эйлер возродил интерес к теоретико-числовым проблемам Диофанта, которые более полувека лежали практически нетронутыми после Ферма.

Метод интегрирующего множителя имел еще одно очень серьезное преимущество. «Предпосылкой широкого употребления метода интегрирующего множителя, по умножению на который уравнение первого порядка преобразуется в уравнение полного дифференциала, являлось умение интегрировать последнее»^[22]. Если Pdx + Qdy = 0 — полный дифференциал, а М — интегрирующий множитель, то уравнение М = 0 будет частным интегралом уравнения Pdx + Qdy = 0, если при этом Р и Q не обращаются в бесконечность. Эйлер выделяет еще одно важное свойство интегрирующего множителя. Если Pdx + Qdy = 0 является полным дифференциалом и не выполняется условие дР/ду = dQ/dx, то уравнение Pdx + Qdy = 0 всегда имеет интегрирующий множитель. Но поиск интегрирующего множителя сопряжен с определенными сложностями. Так, для нахождения интегрирующего множителя Эйлер решал уравнения с частными производными.

Эйлер разобрал еще один важный случай нелинейного дифференциального уравнения. Речь идет об уравнении Риккати. «Уравнение Риккати вызывало интерес у многих исследователей не только потому, что к нему приводит ряд задач механики, но и в силу возможности свести к нему любое линейное уравнение второго порядка»^[23]. Эйлер изучал уравнение Риккати вида dy/dx = Р (х)у^[22] + Q (x)y + R (x) еще начиная с 1730-х гг. Ему удалось показать, что это уравнение можно свести к линейному, если, зная одно частное решение, воспользоваться подстановкой у = v + 1 /2. И более того, если известны два частных решения этого уравнения, то оно вообще интегрируется квадратурой.

Теперь рассмотрим линейные дифференциальные уравнения. Для эфирных концепций и для атомизма были очень важны колебания маятника. Сам по себе маятник может быть использован как модель для изучения эфира. Сам эфир колеблется туда-сюда, но при этом еще присутствует тяжелая материальная точка. Колебания заставляют отклоняться эту точку. Общая траектория и будет описывать криволинейное движение, например круговое.

В XVIII в. в связи с моделью упругого эфира стали описывать не изохронное колебание отдельной точки, а колебание системы любого конечного числа материальных точек. А задача определения колебания струны привела к началу исследования систем с бесконечным числом степеней свободы. Математическая модель упругого эфира подразумевала описание малых колебаний системы с конечным числом степеней свободы, причем в простейшем случае это колебание должно было происходить в отсутствие сопротивления среды. Данную систему малых колебаний эфира описывали линейные дифференциальные уравнения. Кроме того, линейные дифференциальные уравнения второго порядка описывали гравитационные эффекты, создаваемые упругим вращающимся эфиром.

Теорию линейных дифференциальных уравнений Эйлер начал развивать в связи с актуальной задачей математической модели эфира — распространением колебаний в упругой среде. Это и есть задача распространения колебаний в новой модели упругого механического эфира. Эйлер рассмотрел решение однородного линейного дифференциального уравнения, записанного в форме.

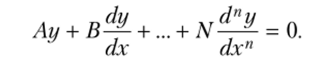
Эйлер решал это дифференциальное уравнение с помощью экспоненциальной подстановки вида у = еР^х, где р — некоторая константа. «Эйлер пришел к так называемому теперь характеристическому уравнению п-и степени А + Вр + Ср² + Dp³ + … + Npⁿ = 0, которое в случае действительных различных корней р_{, р₂, р_п немедленно дает п частных решений еР^х_у е^р2^х,…, е^р«^х и соответственно общее решение. Эйлер подробно разобрал и случаи, когда характеристическое уравнение имеет кратные действительные, а также мнимые корни, причем воспользовался подстановками вида у = e^kxu»^x.

Эйлер решал неоднородные линейные дифференциальные уравнения с помощью метода интегрирующего множителя. «Прием Эйлера заключался в следующем. Он умножал уравнение, например X = Ay + By' + Су», на е^ол а затем принимал, что его интеграл имеет вид Je^mXdx = б?^аг(А'г/ + В’г/'), где А' и В' — неопределенные коэффициенты. Дифференцируя последнее выражение и почленно сравнивая результат с данным дифференциальным ¹

уравнением, он определял три постоянные А В' и а. Тем самым задача сводилась к решению уравнения е~^^хe^CLXXchc = А’у + В’у', порядок которого на единицу ниже, чем у начального. Таким же путем понижался порядок вновь возникшего уравнения и т. д."^[25]

Теперь рассмотрим заслуги Эйлера при решении систем линейных дифференциальных уравнений с постоянными коэффициентами. Эти системы возникли при описании распространения пульсаций через упругую эфирную среду. Эйлер распространяет на системы линейных дифференциальных уравнений с постоянными коэффициентами метод, который он использовал при решении линейных дифференциальных уравнений. Суть этого метода заключается в построении алгебраического характеристического уравнения. При этом при решении непосредственно самого характеристического уравнения Эйлер использует подстановку р = sirup.

Не менее важные результаты Эйлер получил при решении линейных дифференциальных уравнений с постоянными коэффициентами. С такими задачами Эйлер встретился при описании колеблющейся мембраны. Это опять же очень важная частная задача на колебание эфирной среды. Эйлер сумел описать эти колебания с помощью цилиндрических функций, которые являются решениями линейных дифференциальных уравнений с переменными коэффициентами.

Эйлер представляет частное решение уравнения цилиндрических функций в виде некоторого степенного ряда с неопределенными коэффициентами и = Ах*< + Bx^k~ⁿ + Сх^к~^2п + …, после чего он находит условия обрыва этого ряда.

Эйлер предложил еще несколько методов решения линейных дифференциальных уравнений с переменными коэффициентами. Метод канонических преобразований позволяет свести решения ряда таких уравнений к квадратурам. Другой метод основан на применении определенных интегралов, зависящих от параметров.

Степенные и тригонометрические ряды математики эфирной традиции старались вынести не в точные, а в приближенные математические методы. Основная масса задач, которые достались на долю приближенных методов, относилась к небесной механике. «Попытки применить основные уравнения механики к задачам теории планетных движений, именно, к задаче трех тел, сразу привели к изобретению приближенных методов решения дифференциальных уравнений»^[26].

В качестве основного приближенного метода решения Эйлер использовал метод ломаных. Именно этот метод будет весьма распространен в первой половине XIX в. благодаря работам Коши. Следует сказать, что Эйлер очень много внимания уделял сходимости получаемых рядов. Это всегда отличало в выгодную сторону математиков эфирной традиции от математиков-атомистов.

Другим очень перспективным методом приближенного исследования дифференциальных уравнений явился метод малого параметра. Здесь стоит заменить, что атомист Лаплас смог модифицировать эйлеровский метод малого параметра, превратив его в достаточно эффективный атомистический метод. Эйлеровский метод малого параметра возник при решении задач небесной механики. «Самим возникновением этот метод обязан задачам, в которых эксцентриситеты планетных орбит, наклоны плоскостей орбит к плоскости эклиптики и силы тяготения соседних планет представляют собою малые величины»¹.

Приближенное решение планетного движения Эйлер строит в виде разложения функций х и у по эксцентриситету, который в этой задаче берется в качестве малого параметра:

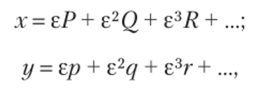
где Р, Q, R,…, р, q> г,… — неизвестные функции, подлежащие дальнейшему определению. «В ряде работ по небесной механике Эйлер для приближенного решения уравнений применяет тригонометрические ряды как для разложения правых частей уравнения, так и для отыскания приближенных решений нелинейных систем в виде неполных тригонометрических рядов. Отметим, что именно эти исследования послужили источником теоретических работ Эйлера об определении коэффициентов разложения функций в тригонометрические ряды»^[27].

Очевидно, что атомист Фурье отталкивался от работ Эйлера при формировании своего принципиально нового взгляда на роль тригонометрических рядов. В этом отношении Эйлер оказал своими исследованиями поддержку в формировании как минимум двух крупных атомистических методов: метода малого параметра Лапласа и метода тригонометрических рядов Фурье.

Здесь же следует сказать, что Эйлер внес серьезный вклад в исследование особых решений дифференциальных уравнений. Опять же особые решения являются более епархией атомизма. Впервые они появились у Тейлора, а наибольший вклад в их исследование внес Лаплас. Для самого же Эйлера особые решения более оставались парадоксами интегрального исчисления. Он так и не смог обнаружить истинную связь между полными и особыми интегралами. Все его усилия были, наоборот, направлены на разграничение этих интегралов.

Теперь перейдем к описанию фундаментального вклада, который внес Эйлер в теории дифференциальных уравнений с частными производными. Задачи, связанные с частными производными, появились при изучении эфирных колебательных процессов. Следует сразу заметить, что и математики эфирной традиции, и атомисты активно использовали аппарат дифференциальных уравнений с частными производными. Но все же основную роль в формировании их теории сыграли представители именно эфирной традиции. В первую очередь речь должна пойти об Эйлере.

Еще в 1730-х гг. Эйлер дал первые представления об этих уравнениях. Он представлял себе решение данного уравнения как пересечение двух семейств кривых, причем все кривые одного семейства пересекают под данным углом кривые другого однопараметрического семейства. С помощью уравнения это можно записать следующим образом:

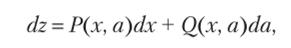
где dz (x, а)/дх = Р (х, а), а дг (х, а)/да = Q (x, а). В этих уравнениях а является вышеупомянутым параметром. Левая часть уравнения описывает пересекающие кривые первого семейства, правая часть — пересекаемые кривые второго семейства.

Очень скоро оказалось, что дифференциальные уравнения в частных производных имеют фундаментальное значение для теории упругого колеблющегося эфира. В конце 1740-х гг. Даламбер и Эйлер практически одновременно дали дифференциальные уравнения колебания струны. «Эйлер первый понял, что уравнение колебания струны отражает процесс распространения волн. Волной при этом называют процесс передвижения отклонения какой-либо точки струны по струне»^[28].

Эйлер записывает дифференциальное уравнение струны в виде d^[29]y/dt^[29] = = а^[29]д^[29]у/дх^[29], а затем выписывает решение этого уравнения: у = ф (х + at) + + |/(х + at). Компонента ф (х + at) означает волну, которая движется со скоростью а в положительную сторону оси абсцисс, а компонента ф (х + at) — такую же волну, но только движущуюся в противоположном направлении. Общее движение струны подразумевает наложение указанных двух воли. Если же ввести новые переменные и = ф (х + at) wv- ф (х + at), то уравнение колебания струны можно привести к весьма удобному для интегрирования виду d^[29]y/dudv = 0.

Эйлер особо обращал внимание на начальную форму струны. Эта форма, но Эйлеру, может быть любой разрывной или смешанной функцией, начерченной «свободным влечением руки». Ни Даламбер, ни Д. Бернулли не были в этом вопросе согласны с Эйлером. В свою очередь, Эйлер активно возражал против решения Д. Бернулли уравнения струны в виде тригонометрического ряда. «Хотя сам Эйлер в конце статьи „О колебании струны“ также дал решение частного случая задачи в виде тригонометрического ряда, он полагал, что тригонометрический ряд не годится для представления даже произвольной алгебраической функции, так как такая функция непериодична и необязательно нечетная, в то время как ряд является периодической и нечетной функцией»^[29].

Не менее важны были для построения новой теории упругого эфира исследования Эйлера по гидродинамике. В середине 1750-х гг. Эйлер вывел основные уравнения гидродинамики для жидкости, лишенной вязкости. Эти уравнения выписаны для любой точки жидкости и характеризуют в любой момент времени скорость движения и давление жидкости. Вот эти уравнения:

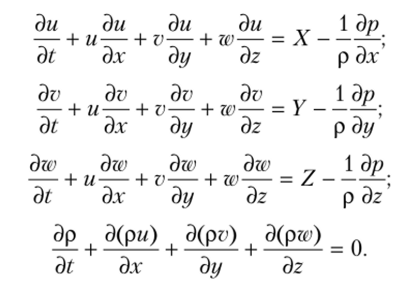
Последнее уравнение может быть преобразовано в уравнение несжимаемой жидкости при р = const:

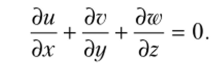
Хорошо известно, что уравнения гидродинамики не интегрируются в общем виде. Поэтому интегрирование возможно только в различных частных случаях движения жидкости и газа. Эйлер начал рассмотрение решений гидродинамических уравнений с простейшего случая плоского потенциального движения идеальной несжимаемой жидкости. Это и есть простейшая модель нового механического эфира. В рамках этой модели плотность является константой, а третья координата скорости становится равной нулю. Потенциальность движения описывается через полные дифференциалы udy — vdx и udx + vdy.

Основным методом интегрирования дифференциальных уравнений в частных производных первого порядка являлось сведение к уравнениям в полных дифференциалах. А уравнение в полных дифференциалах к этому времени уже вполне умели решать.

В 1760 г. Эйлер получил систему волновых уравнений звуковых колебаний в виде.

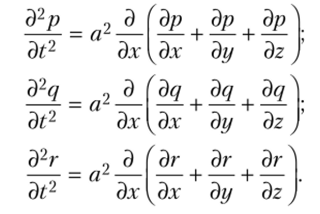
Но эти уравнения в общем виде Эйлеру не удалось проинтегрировать. Интегрирование получилось лишь для случая сферических волн, когда движение направлено от некоторого фиксированного центра, при этом скорости в равноудаленных точках одинаковы.

Эйлер также рассмотрел задачу о движении воздуха в трубе постоянного сечения (плоские звуковые волны). Другим важным примером дифференциальных уравнений в частных производных стали задачи о движении струн переменной толщины и о колеблющейся мембране. Последняя задача была сведена к уравнению цилиндрических волн.

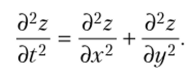
Эйлер исследовал уравнения колебаний прямоугольной и круглой мембраны. При этом он нашел полную систему собственных колебаний этих мембран.

Теперь следует сказать несколько слов о связи исследований Эйлера в области дифференциальных уравнений и диофантовым анализом. Вот что об этой связи пишет И. Г. Башмакова: «Заметим, что подстановки Диофанта по методам А и В совпадают с так называемыми подстановками Эйлера, применяемыми при интегрировании дифференциалов вида.

Разница состоит лишь в том, что Диофант проводит все.

yjaX^[36][37] +ЪХ + с

выкладки над нолем Q рациональных чисел, тогда как подстановки Эйлера можно применять и тогда, когда а и с не являются квадратами, т. е. 4а и 4с иррациональны"¹. Этот небольшой фрагмент явно свидетельствует о связи методов диофантовой традиции и эйлеровскими математическими методами. Думается, что подробное сопоставление методов Диофанта и Эйлера открыло бы многие внутренние связи в математике XVIII в.

• [1] История математики с древнейших времен до начала XIX века. Т. 3. С. 241.
• [2] Спасский Б. И. Указ. соч. Т. 1. С. 156.
• [3] История математики с древнейших времен до начала XIX века. Т. 3. С. 265.
• [4] Там же С. 257.
• [5] Там же С. 257.
• [6] Там же С. 257.
• [7] Там же С. 257.
• [8] Там же С. 257.
• [9] Там же С. 257.
• [10] Эйлер Л.

  Введение

  в анализ бесконечных. В 2 т. М., 1961. Т. 1. С. 67.

• [11] Эйлер Л.

  Введение

  в анализ бесконечных. Т. 2. С. 275—276.

• [12] Эйлер Л.

  Введение

  в анализ бесконечных. Т. 2. С. 275—276.

• [13] Эйлер Л.

  Введение

  в анализ бесконечных. Т. 2. С. 275—276.

• [14] Эйлер Л.

  Введение

  в анализ бесконечных. Т. 2. С. 275—276.

• [15] Эйлер Л.

  Введение

  в анализ бесконечных. Т. 2. С. 275—276.

• [16] Эйлер Л.

  Введение

  в анализ бесконечных. В 2 т. М., 1961. Т. 1. С. 67.

• [17] История математики с древнейших времен до начала XIX века. Т. 3. С. 252.
• [18] Эйлер Л. Интегральное исчисление. В 3 т. М., 1958. Т. 3. С. 28.
• [19] Эйлер Л. Дифференциальное исчисление. М.; Л., 1949. С. 39.
• [20] Там же. С. 41.
• [21] История математики с древнейших времен до начала XIX века. Т. 3. С. 375.
• [22] Там же. С. 375.
• [23] Там же. С. 377.
• [24] Там же. С. 375.
• [25] Вилейтнер Г. Указ. соч. С. 172.
• [26] Там же. С. 178.
• [27] Там же. С. 396.
• [28] История математики с древнейших времен до начала XIX века. Т. 3. С. 415.
• [29] Там же. С. 418.
• [30] Там же. С. 418.
• [31] Там же. С. 418.
• [32] Там же. С. 418.
• [33] Там же. С. 418.
• [34] Там же. С. 418.
• [35] Там же. С. 418.
• [36] Диофант. Арифметика и книга о многоугольных числах. Комментарии И. Г. Башма-
• [37] ковой. С. 191.