Средние величины. 
Теория вероятностей и математическая статистика

Средние величины характеризуют значения признака, вокруг которого концентрируются наблюдения или, как говорят, центральную тенденцию распределения. Наиболее распространенной из средних величин является средняя арифметическая.

Определение. Средней арифметической вариационного ряда называется сумма произведений всех вариантов на соответствующие частоты, деленная на сумму частот:

где Xj — варианты дискретного ряда или середины интервалов интервального вариационного ряда; п, — соответствующие им частоты; т —.

т

число неповторяющихся вариантов или число интервалов; n = Y,ⁿi ?

1=1.

Очевидно, что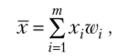

где Wj = п,/п — частости вариантов или интервалов.

|> Пример 8.3. Найти среднюю выработку рабочих по данным табл. 8.1. Решение. По формуле (8.2) для интервального вариационного ряда.

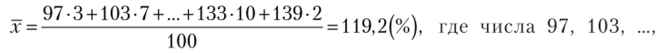
133, 139 — середины соответствующих интервалов. ?

Для несгруппированного ряда все частоты щ- 1 (г = 1, 2,…, п), а.

есть «невзвешенная» средняя арифметическая.

Отметим основные свойства средней арифметической, аналогичные свойствам математического ожидания случайной величины.

• 1. Средняя арифметическая постоянной равна самой постоянной.
• 2. Если все варианты увеличить (уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз:

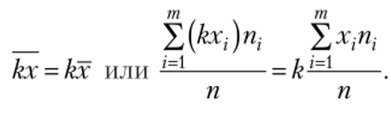
3. Если все варианты увеличить (.уменьшить) на одно и то же число, то средняя арифметическая увеличится {уменьшится) 7ia то же число:

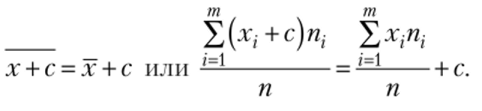
4. Средняя арифметическая отклонений вариантов от средней арифметической равна нулю:

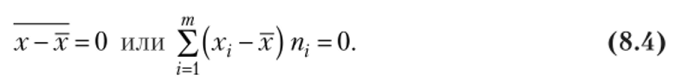
• ? При с-х х-с = х-с = х-х = 0. ?
• 5. Средняя арифметическая алгебраической суммы нескольких признаков равна такой же сумме средних арифметических этих признаков:

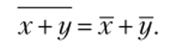
6. Если ряд состоит из нескольких групп, общая средняя равна средней арифметической групповых средних, причем весами являются объемы групп:

где х — общая средняя (средняя арифметическая всего ряда); x_i — групповая средняя ?*-й группы, объем которой равен /г,; / — число групп.

При решении практических задач могут применяться и иные формы средней, которые можно получить из средней степенной k-го порядка^]:

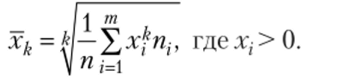
Легко убедиться в том, что при k = 1 получаем формулу средней арифметической. При других значениях k получаем формулы:

_.

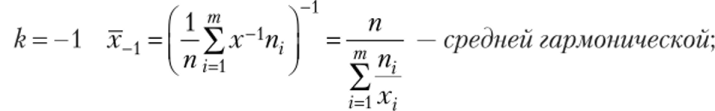
(1 ^т V'.

~Yl^xiⁿi 9 ^{так как} корень k-i степени определяется.

^п i= J

k — О (после раскрытия неопределенности при вычислении предела.

1 im x_k) х₀ = Jx" ¹ x'}² …хЦ'" = JП x"‘ — средней геометрической; k-+o «V ,=i.

Можно показать, что с ростом порядка k степенная средняя возрастает, т. е. х_] 0t2 <… (свойство мажорантности средних).

Кроме рассмотренных средних величин, называемых аналитическими, в статистическом анализе применяют структурные, или порядковые, средние. Из них наиболее широко применяются медиана и мода.

Определение. Медианой Me вариационного ряда называется значение признака, приходящееся на середину ранжированного ряда наблюдений.

Для дискретного вариационного ряда с нечетным числом членов медиана равна серединному варианту, а для ряда с четным числом членов — полусумме двух серединных вариантов.

О Пример 8.4. Найти медиану распределения рабочих по тарифному разряду по данным табл. 8.2.

Решение, п = 50 — четное, следовательно, серединных вариантов два: х₂₅ = 5 и x₂f,=5. Поэтому Me = (х₂₅ + х₂₆)/2 = (5 + 5)/2 = 5 (%). ?

Для интервального вариационного ряда находится медианный интервал, на который приходится середина ряда, а значение медианы на этом интервале находят с помощью линейного интерполирования. Не приводя соответствующей формулы, отметим, что медиана может быть приближенно найдена с помощью кумуляты как значение признака, для которого п"^ак= п/2 или <^ак= ½.

Достоинство медианы как меры центральной тенденции заключается в том, что на нее не влияет изменение крайних членов вариационного ряда, если любой из них, меньший медианы, остается меньше ее, а любой, больший медианы, продолжает быть больше ее. Медиана предпочтительнее средней арифметической для ряда, у которого крайние варианты по сравнению с остальными оказались чрезмерно большими или малыми.

Определение. Модой Мо вариационного ряда называется вариант, которому соответствует наибольшая частота.

Например, для вариационного ряда табл. 8.2 мода Мо = 5, так как этому варианту соответствует наибольшая частота n_t = 22. Для интервального ряда находится модальный интервал, имеющий наибольшую частоту, а значение моды на этом интервале определяют с помощью линейного интериолирования. Однако проще моду можно найти графическим путем с помощью гистограммы.

Особенность моды как меры центральной тенденции заключается в том, что она не изменяется при изменении крайних членов ряда, т. е. обладает определенной устойчивостью к вариации признака.

О Пример 8.5. Найти медиану и моду распределения рабочих, но выработке по данным табл. 8.1.

Решение. На рис. 8.2, 6 проведем горизонтальную прямую у — 0,5 (или у = 50), соответствующую накопленной частости ш" ^ак = F"(x)= 0,5 (или накопленной частоте га"^ак= 50), до пересечения с графиком эмпирической функции распределения (или кумулятой). Абсцисса точки пересечения и будет медианой вариационного ряда: Me = 119,9(%).

На гистограмме распределения (см. рис. 8.2, а) находим прямоугольник с наибольшей частотой (частостью). Соединяя отрезками прямых вершины этого прямоугольника с соответствующими вершинами двух соседних прямоугольников (см. рис. 8.2, а), получим точку пересечения этих отрезков (диагоналей), абсцисса которой и будет модой вариационного ряда: Мо =120,8(%). ?